Zu ergründen, ob das Universum nun endlich oder unendlich groß ist, warf für die ersten Kosmologen stets Ungereimtheiten auf, wenn sie versuchten, sich der Materie nach den Gesetzen der Logik zu nähern. Dabei war das nach Richard Bentley – einem Zeitgenossen Newtons – benannte Paradoxon eines der am häufigsten auftretenden Probleme. Bentley war ein Gelehrter, der wie viele Wissenschaftler seiner Zeit in Diensten der Kirche stand und später Rektor des Trinity College in Cambridge wurde. Obwohl er Altphilologe und Theologe war, lehrte Bentley Ende des 17. Jahrhunderts eine Zeitlang Newton’sche Physik und ging mit Newton in einer ganzen Reihe von Fragen konform, so auch in der seines Paradoxons.

Mit der Verbreitung von Newtons Gravitationsgesetzen schienen sich verheerende Folgen für die Kosmologie anzubahnen. Zögen sich alle Objekte gegenseitig an, wie Newton behauptete, wäre es laut Bentley nur eine Frage der Zeit, bis jeder Stern oder Planet zu seinem Nachbarn hingezogen würde und auf diese Weise schließlich das gesamte Universum in sich zusammenbräche. Und wäre das Universum unendlich groß, ließe dies noch Schlimmeres befürchten. In diesem Fall könnte die Summe der Schwerkraft selbst unendlich sein, weshalb Objekte wie die Erde oder die Sonne unmöglich existieren könnten und von der Schwerkraft mit brachialer Gewalt in Stücke gerissen würden.

Dieses Szenario einer unendlich großen Schwerkraft war jedoch realitätsferner als das Problem eines kollabierenden Universums – nicht nur, weil niemand wusste, ob das Universum unendlich groß ist, sondern auch aufgrund eines mathematischen Kniffs, der bereits den alten Griechen geläufig war, seitdem Zenon anhand eines imaginären Wettlaufs zwischen dem griechischen Helden Achilles und einer Schildkröte ein Paradoxon beschrieben hatte.

Achilles, der wohl schnellste Mensch seiner Zeit und das antike Pendant eines Sportstars von heute, tritt in einem Wettlauf gegen eine Schildkröte an. Betrachtet man den Ausgang eines ganz ähnlichen Wettrennens in einer von Äsops Fabeln (die nur Jahrzehnte vor Zenons Paradoxa entstanden), überrascht es nicht allzu sehr, dass die Schildkröte gewinnt. Aber im Gegensatz zum Ausgang des Wettrennens zwischen der Schildkröte und dem Hasen bei Äsop ist dieses unwahrscheinliche Ergebnis nicht der Faulheit und der Überheblichkeit geschuldet. Vielmehr bemüht Zenon die reine Bewegungsmechanik, um die Schildkröte schließlich zum Sieger zu küren.

Zenon geht von der Annahme aus, dass Achilles so fair sei, der Schildkröte einen Vorsprung zu gewähren; dennoch kann von einem Rennen unter Gleichen keine Rede sein, schließlich war Achilles zu jener Zeit ein wahrer Held. Achilles räumt der Schildkröte also einen beträchtlichen Vorsprung ein. Schon nach kürzester Zeit – Achilles war ein ausgezeichneter Läufer – hat unser Star-Sprinter den Startpunkt der Schildkröte erreicht. Allerdings hat in dieser Zeit auch die Schildkröte, so langsam sie auch dahinkriechen mag, ein kleines Stück der Wegstrecke bewältigt und liegt immer noch in Führung. In noch kürzerer Zeit erreicht Achilles nun die zweite Position der Schildkröte, doch auch die Schildkröte hatte in dieser zusätzlichen Zeitspanne erneut die Möglichkeit, sich fortzubewegen. Auf diese Weise setzt sich das Rennen – mathematischer Logik gehorchend – endlos lange fort, sodass Achilles der Schildkröte stets dicht auf den Fersen ist, sie jedoch nie einholt.

Dieses Paradoxon zeigt, dass es unendliche geometrische Reihen geben kann, deren Summe einen unendlich großen Wert annimmt. Denken wir nur an die Addition folgender Reihe:

Mit jedem neuen Glied in der Reihe nähert sich deren Summe ein Stück mehr dem Wert 2, ohne diesen jedoch jemals zu erreichen. Die Gesamtsumme der Reihe beträgt nach jeder Addition:

Stellen wir uns vor, wir setzten unsere Reihe milliardenfach fort, bis wir den Term n erreichten. In diesem Fall betrüge die Gesamtsumme 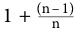. Werden die Glieder einer Reihe schnell genug kleiner, ergibt deren Summe nur eine endliche Zahl. So können wir in unserer Reihe beliebig viele Glieder addieren – ja sogar eine unendliche Anzahl von Gliedern – und werden in der Summe dennoch nie den Wert 2 übertreffen.

Eine endliche geometrische Reihe dieser Art könnte die These rechtfertigen, dass ein unendlich großes Universum aufgrund der Art und Weise, wie die Schwerkraft mit zunehmender Distanz von einem Objekt abnimmt, keine unendlich großen Kräfte aufbieten muss. Die Schwerkraft nimmt schnell genug ab, um eine geometrische Reihe dieser Art zu erzeugen, es könnte also sein, dass unendlich viele Sterne und Planeten nur eine begrenzte Anziehungskraft ausüben müssen. Dies würde jedoch Bentleys ursprüngliches Problem nicht lösen, warum nicht alle Sterne und Planeten in einer Art Massenkarambolage universalen Ausmaßes miteinander kollidierten.

Newton freilich war ein Verfechter der These eines unendlich großen Universums und wies Bentley darauf hin, dass sein Paradoxon nicht unbedingt eintreten müsse, wenn alle Objekte im Universum gleichmäßig verteilt wären, sodass sich die Anziehungskräfte nach allen Seiten gegenseitig neutralisierten und ein kräftemäßiges Gleichgewicht bestünde. Allerdings war sich Newton darüber im Klaren, wie instabil dieses Szenario ist, bedurfte es doch lediglich einer kleinen Verschiebung eines einzigen Planeten oder Sterns, um sämtliche Objekte mit zunehmendem Momentum ineinanderkrachen zu lassen.

Zur Lösung dieses Problems wandte sich Newton Gott zu. Wie die meisten Wissenschaftler seiner Zeit war er tief religiös, auch wenn seine Vorstellung vom christlichen Glauben alles andere als konventionell war. Aus seiner Sicht stellte diese potenzielle Instabilität kein Problem dar, lenkte Gottes Hand doch die Geschicke des Universums und war jederzeit in der Lage, minimale Kurskorrekturen vorzunehmen, um den Fortgang des Universums zu gewährleisten.