5. PRUEBA POR CONTRADICCIÓN
Las construcciones de los matemáticos, como las de los pintores o los poetas, deben ser bellas; las ideas, como los colores o las palabras, deben encajar con armonía. La belleza es el primer requisito: no hay un lugar permanente en el mundo para las matemáticas feas.
G. H. Hardy
En enero de 1954, un brillante y joven matemático de la Universidad de Tokio fue a la biblioteca de su departamento. Goro Shimura buscaba una copia del volumen 24 de Matematische Annalen. En particular estaba buscando un artículo de Deuring sobre su teoría algebraica de la multiplicación compleja, que necesitaba como ayuda para un cálculo particularmente difícil y esotérico.
Para su sorpresa y consternación, alguien se había llevado ya el volumen. Quien lo había tomado en préstamo era Yutaka Taniyama, un conocido lejano de Shimura que vivía al otro lado del campus. Shimura escribió a Taniyama explicando que necesitaba la revista con urgencia para completar el complejo cálculo y le preguntó educadamente cuándo la devolvería.
Pocos días más tarde apareció una carta en la mesa de Shimura. Taniyama había contestado diciendo que también él estaba trabajando en aquel mismo cálculo y que estaba atascado en el mismo paso lógico. Sugirió que podían compartir sus ideas y tal vez colaborar en el problema. Este casual encuentro gracias a un libro de la biblioteca inició una colaboración que cambiaría el curso de la historia de las matemáticas.
Taniyama nació el 12 de noviembre de 1927 en una pequeña ciudad a unos pocos kilómetros al norte de Tokio. La grafía japonesa usada para representar su nombre debería leerse «Toyo», pero la mayoría de las personas ajenas a su familia lo malinterpretaron como «Yutaka» y, al crecer, Taniyama asumió y adoptó ese apelativo. Durante su infancia la educación de Taniyama se interrumpió constantemente. Padeció varias enfermedades y durante la pubertad sufrió un ataque de tuberculosis y perdió dos años de instituto. El inicio de la guerra causó una interrupción aún mayor en su escolaridad.
Goro Shimura, un año más joven que Taniyama, también vio interrumpida su escolarización durante los años de la guerra. Su escuela fue clausurada y, en lugar de asistir a clase, Shimura tuvo que ayudar al esfuerzo bélico trabajando en una fábrica donde montaba piezas de aviones. Estudiaba cada tarde para corregir su falta de instrucción escolar y se sintió particularmente atraído por las matemáticas. «Por supuesto, hay muchas materias para aprender, pero las matemáticas eran las más sencillas porque podía limitarme a leer libros de texto de matemáticas. Aprendí cálculo leyendo libros. Si hubiera querido aprender química o física habría necesitado instrumental científico y yo no tenía acceso a tales cosas. Nunca creí poseer talento. Sólo era curioso».
Unos pocos años después de la guerra, Shimura y Taniyama se encontraron en la universidad. En la época en que se intercambiaron las cartas sobre el libro de la biblioteca, la vida en Tokio volvía a la normalidad y los dos jóvenes universitarios podían permitirse uno o dos pequeños lujos. Pasaban las tardes en cafeterías, por las noches cenaban en un pequeño restaurante especializado en carne de ballena y durante los fines de semana paseaban por los jardines botánicos o por el parque de la ciudad. Todos eran lugares ideales para comentar sus más recientes pensamientos matemáticos.
Si bien Shimura tenía una vena fantasiosa, era mucho más conservador y convencional que su compañero intelectual. Shimura se levantaba al alba y se ponía a trabajar de inmediato, mientras que su colega a menudo estaba aún despierto tras haber trabajado durante toda la noche. Quienes visitaban el apartamento de Taniyama a menudo lo encontraban dormido a media tarde.
Mientras que Shimura era puntilloso, Taniyama era descuidado hasta el punto de la vagancia. Sorprendentemente, éste era el aspecto que Shimura admiraba: «Tenía el don de cometer muchos errores, casi siempre en la dirección correcta. Lo envidiaba por ello y traté en vano de imitarlo, pero me resultó muy difícil cometer buenos errores».
Taniyama era el epítome del genio de mente ausente, y esto se reflejaba en su apariencia. Era incapaz de hacer un nudo decente, y por ello decidió que en lugar de anudarse los cordones de sus zapatos una docena de veces al día no los iba a anudar nunca. Siempre vestía el mismo traje verde tan peculiar, con un extraño brillo metálico. El resto de su familia lo había rechazado porque estaba hecho de una tela muy llamativa.
Cuando se encontraron en 1954, Taniyama y Shimura estaban empezando sus carreras en matemáticas. La tradición era, y aún es, que los investigadores jóvenes se refugiaran bajo el ala de algún profesor que los ayudara en el entrenamiento mental, pero Taniyama y Shimura rechazaron esta forma de aprendizaje. Durante la guerra, la investigación real se había detenido, e incluso en los años cincuenta la Facultad de Matemáticas aún no se había recuperado. Según Shimura, los profesores estaban «cansados, hastiados y desilusionados». En comparación, los estudiantes de la posguerra eran apasionados y estaban impacientes por aprender, y pronto se dieron cuenta de que el único modo de progreso era aprender por sí mismos. Los estudiantes organizaron seminarios regulares, dándolos por turno para informar al resto de las últimas técnicas y avances. A pesar de su pereza habitual, Taniyama proporcionaba gran empuje cuando asistía a los seminarios. Animaba a los estudiantes mayores a explorar territorios desconocidos y actuaba como una figura paternal para los estudiantes más jóvenes.
Debido a su aislamiento, los seminarios trataban ocasionalmente temas que se consideraban superados en Europa y América. La ingenuidad de los estudiantes significaba que estudiaban ecuaciones que habían sido abandonadas en Occidente. Un tema particularmente pasado de moda que fascinó a Taniyama y Shimura fue el estudio de las formas modulares.
Las formas modulares son unos de los objetos más misteriosos y maravillosos de las matemáticas. Se hallan entre las entidades más esotéricas de las matemáticas y, aun así, el teórico de los números del siglo XX Martin Eichler las contó como una de las cinco operaciones fundamentales: suma, resta, multiplicación, división y formas modulares. La mayor parte de los matemáticos se consideran maestros de las cuatro primeras operaciones, pero encuentran algo confusa la quinta.
La característica clave de las formas modulares es su desmedido grado de simetría. Aunque la mayor parte de la gente está familiarizada con el concepto común de simetría, ésta tiene un significado especial en matemáticas: un objeto tiene simetría si se puede transformar de un modo particular y después de la transformación permanece inalterado. Para apreciar la inmensa simetría de una forma modular conviene examinar primero la de un objeto más mundano, como un simple cuadrado.
En el caso de un cuadrado, una forma de simetría es la rotacional. Es decir, si imaginamos un pivote en el punto donde se cruzan los ejes x e y, entonces el cuadrado de la figura 18 se puede rotar un cuarto de vuelta y después parecerá que no se ha transformado. De forma similar, las rotaciones de media vuelta, tres cuartos de vuelta y una vuelta completa dejarán también aparentemente inalterado el cuadrado.
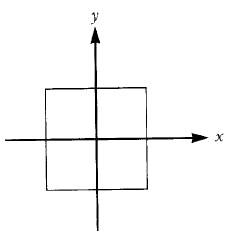
Figura 18: Un simple cuadrado exhibe tanto simetría rotacional como por reflexión.
Además de la simetría rotacional, el cuadrado también posee simetría por reflexión. Si imaginamos un espejo situado a lo largo del eje x, entonces la parte superior del cuadrado se reflejaría exactamente sobre la mitad inferior, y viceversa, de manera que tras la transformación el cuadrado parecería no haber cambiado. De forma similar podemos definir otros tres espejos (a lo largo de las dos diagonales y a lo largo del eje y) para los cuales el cuadrado reflejado parecería idéntico al original.
El simple cuadrado es bastante simétrico, ya que posee simetría rotacional y por reflexión, pero no posee ninguna simetría translacional. Esto significa que si el cuadrado se desplazara en cualquier dirección, un observador podría detectar el movimiento inmediatamente porque su posición relativa a los ejes habría cambiado. Sin embargo, si todo el espacio estuviera recubierto por cuadrados, como se muestra en la figura 19, esta colección infinita de cuadrados tendría simetría translacional. Si la superficie infinitamente teselada se desplazara arriba o abajo por espacio de una o más teselas, ese teselado parecería idéntico al original.
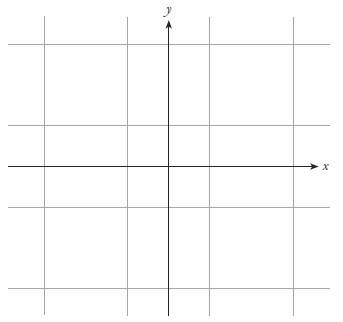
Figura 19: Una superficie infinita recubierta de cuadrados exhibe simetría rotacional y por reflexión, y además, tiene simetría translacional.
La simetría de las superficies teseladas es una idea bastante clara pero, como muchos otros conceptos aparentemente simples, esconde varias sutilezas. Por ejemplo, en la década de los setenta el físico y matemático recreativo británico Roger Penrose empezó a jugar con diferentes teselas sobre la misma superficie. Al fin identificó dos formas particularmente interesantes, llamadas la cometa y la punta de flecha, que se muestran en la figura 20. Por separado, cada una de estas teselas no se puede usar para recubrir una superficie sin dejar huecos o producir superposiciones, pero juntas se pueden emplear para crear un rico conjunto de modelos de teselación. Las cometas y puntas de flecha se pueden encajar unas en otras en un número infinito de formas y, aunque en apariencia cada modelo es similar, en detalle todos ellos son distintos. En la figura 20 se muestra el modelo creado con cometas y puntas de flecha.
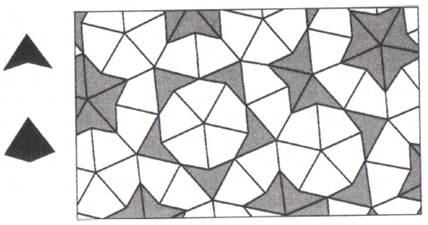
Figura 20: Usando dos teselas diferentes, la cometa y la punta de flecha, Roger Penrose pudo recubrir una superficie. Sin embargo, la teselación de Penrose no posee simetría translacional.
Otra característica singular de las teselaciones de Penrose (los recubrimientos generados por teselas tales como la cometa y la punta de flecha) es que su nivel de simetría es muy restringido. A primera vista parece que la teselación mostrada en la figura 20 posee simetría translacional, pero cualquier intento de desplazar el teselado a lo largo de la superficie de modo que permanezca inalterado acaba en fracaso. Los recubrimientos de Penrose son decepcionantemente asimétricos y por eso fascinan a los matemáticos y se han convertido en el punto de partida de un área completamente nueva de las matemáticas.
Es curioso que los recubrimientos de Penrose también hayan tenido repercusiones en la ciencia de los materiales. Los cristalógrafos siempre habían creído que los cristales tenían que construirse según los principios de la teselación cuadrada, que posee un alto nivel de simetría translacional. En teoría, la construcción de cristales se basaba en una estructura muy regular y repetitiva. Sin embargo, en 1984 los científicos descubrieron un cristal metálico formado por aluminio y manganeso que estaba construido según los principios de Penrose. El mosaico de aluminio y manganeso se comporta como las cometas y puntas de flecha, generando un cristal casi regular, pero no del todo. Una empresa francesa ha desarrollado recientemente un cristal de Penrose como recubrimiento para sartenes.
Aunque lo fascinante de las teselaciones de Penrose se encuentra en su restringida simetría, la propiedad más interesante de las formas modulares es que exhiben una simetría infinita. Las formas modulares estudiadas por Shimura y Taniyama se pueden desplazar, invertir, intercambiar, reflejar y rotar en un número infinito de maneras y siempre permanecen inalteradas, lo que hace de ellas los objetos matemáticos más simétricos. Cuando el erudito francés Henri Poincaré estudió las formas modulares en el siglo XIX tuvo una gran dificultad para expresar su inmensa simetría. Tras trabajar en un tipo particular de forma modular, describió a sus colegas cómo cada día, durante dos semanas, se despertaba y buscaba un error en sus cálculos. Al decimoquinto día llegó a la conclusión de que sus cálculos eran correctos y aceptó que las formas modulares eran en efecto extremadamente simétricas.
Por desgracia, dibujar, o incluso imaginar, una forma modular es imposible, en el caso de un cuadrado estamos en presencia de un objeto de dos dimensiones, con un espacio definido por los ejes x e y. Una forma modular también está definida por dos ejes, pero los dos son complejos; es decir, cada eje posee una parte real y otra imaginaria, y en realidad se compone de dos ejes. Por lo tanto, el primer eje complejo se debe representar por dos ejes, xr (real) y xi (imaginario), y el segundo eje se representa por otros dos ejes, yr (real) e yi (imaginario). Para ser precisos, las formas modulares habitan en el semiplano superior de este espacio complejo, pero lo que es más importante es darse cuenta de que este espacio es tetradimensional (xr, xi, yr, yi).
Este espacio de cuatro dimensiones es el llamado espacio hiperbólico. El espacio hiperbólico es difícil de entender para los humanos, que están constreñidos a vivir en el mundo convencional de tres dimensiones, pero el espacio de cuatro dimensiones es un concepto matemáticamente válido, y es esta dimensión adicional la que proporciona a las formas modulares un nivel tan elevado de simetría. El artista Mauritz Escher quedó fascinado por las ideas matemáticas e intentó transmitir el concepto de espacio hiperbólico en algunos de sus aguafuertes y pinturas. La figura 21 muestra la obra Circle Limit IV de Escher, que incrusta el mundo del espacio hiperbólico en la página bidimensional. En el espacio hiperbólico real, los murciélagos y los ángeles serían todos del mismo tamaño, y la repetición es indicativa del alto grado de simetría. Aunque parte de la simetría se puede apreciar en la página bidimensional, existe una distorsión creciente hacia el borde de la pintura.

Figura 21: La obra Circle Limit IV, de Mauritz Escher, da una idea de la simetría de las formas modulares.
Las formas modulares que habitan el espacio hiperbólico son de varias formas y tamaños, pero cada una está construida con los mismos ingredientes básicos. Lo que diferencia cada forma modular es la cantidad de cada uno de los ingredientes que la componen. Los ingredientes que componen una forma modular están etiquetados de uno a infinito (M1, M2, M3, M4,…), y así cada forma modular particular puede contener una medida del ingrediente uno (M1 = 1), tres medidas del ingrediente dos (M2 = 3), dos medidas del ingrediente tres (M3 = 2), etc. Esta información que describe cómo construir una forma modular se puede resumir en la llamada serie modular, o serie M, una lista de los ingredientes y la cantidad requerida de cada uno:
| Serie M: M1 | = 1, |
| M2 | = 3, |
| M3 | = 2, |
| ↓ |
Del mismo modo que la serie E es el ADN para las ecuaciones elípticas, la serie M lo es para las formas modulares. La cantidad de cada ingrediente listada en la serie M es crítica. Dependiendo de cuánto se cambie la cantidad, por decir algo, del primer ingrediente, se genera una forma modular del todo diferente, aunque igualmente simétrica, o se puede destruir la simetría y generar un nuevo objeto que no es una forma modular. Sí la cantidad de cada ingrediente se escoge de manera arbitraria, entonces el resultado será probablemente un objeto con poca o ninguna simetría.
Las formas modulares constituyen casi un mundo aparte dentro de las matemáticas. En particular parecían completamente ajenas al tema que Wiles estudiaría más adelante en Cambridge, las ecuaciones elípticas. La forma modular es una bestia enormemente complicada, estudiada sobre todo por su simetría y descubierta en el siglo XIX. Las ecuaciones elípticas se remontan a los antiguos griegos y no tienen nada que ver con las simetrías. Las formas modulares y las ecuaciones elípticas habitan regiones completamente diferentes del cosmos matemático y nadie hubiera creído que existiera la menor relación entre los dos temas. Sin embargo, Taniyama y Shimura sorprenderían a la comunidad matemática al sugerir que las ecuaciones elípticas y las formas modulares son en realidad una sola cosa. Según esos maravillosos matemáticos, ellos podían unificar los mundos modular y elíptico.
Ilusiones y espejismos
En septiembre de 1955 se celebró un simposio internacional en Tokio. Fue una oportunidad única para los muchos jóvenes investigadores japoneses de mostrar al resto del mundo lo que habían aprendido. Repartieron una colección de treinta y seis problemas relacionados con su trabajo, acompañada por una humilde introducción: Algunos problemas sin resolver en matemáticas: no se ha realizado una preparación madura, de modo que puede haber algunos triviales o ya resueltos entre ellos. Se solicita a los participantes que hagan comentarios sobre cualquiera de estos problemas.
Cuatro de estas cuestiones eran de Taniyama, y daban pistas sobre una curiosa relación entre las formas modulares y las ecuaciones elípticas. Estas inocentes preguntas llevarían finalmente a una revolución en la teoría de números. Taniyama se había fijado en los primeros términos de la serie M de una forma modular en particular. Reconoció la sucesión y se dio cuenta de que era idéntica a la lista de números de la serie E de una ecuación elíptica bien conocida. Calculó algunos términos más de cada una de las series y la serie M de la forma modular y la E de la ecuación elíptica continuaban encajando perfectamente.
Fue un descubrimiento sorprendente porque, sin razón aparente, esa forma modular podía estar relacionada con una ecuación elíptica a través de sus respectivas series M y E: las series eran idénticas. El ADN matemático que construye cada una de esas dos entidades era exactamente el mismo. Este fue un descubrimiento doblemente valioso. En primer lugar sugería que, profundamente enterrada, había una relación fundamental entre la forma modular y la ecuación elíptica, objetos que provienen de extremos opuestos de las matemáticas. En segundo lugar significaba que los matemáticos, que ya conocían las series M de las formas modulares, no necesitaban calcular las series E porque eran las mismas que las series M.
Las relaciones entre temas aparentemente diferentes son tan importantes para la creatividad en matemáticas como en cualquier otra disciplina. La relación es una pista sobre alguna verdad oculta que enriquece ambos temas. Por ejemplo, al principio los científicos estudiaron la electricidad y el magnetismo como dos fenómenos completamente separados. En el siglo XIX, los teóricos y los experimentales se dieron cuenta de que la electricidad y el magnetismo estaban íntimamente relacionados. Este descubrimiento llevó a una comprensión más profunda de ambos fenómenos. Las corrientes eléctricas generan campos magnéticos y los imanes pueden inducir electricidad en cables que pasen cerca de ellos. Esto condujo a la invención de las dinamos y los motores eléctricos, y por fin al descubrimiento de que la luz misma es el resultado de campos eléctricos y magnéticos oscilando armónicamente.
Taniyama examinó algunas otras formas modulares y en cada caso la serie M parecía corresponder perfectamente con la serie E de una ecuación elíptica. Empezó a preguntarse si podría ser que cada forma modular pudiera asociarse a una ecuación elíptica. Tal vez cada forma modular tuviera el mismo ADN que una ecuación elíptica: ¿tal vez cada forma modular fuera una ecuación elíptica disfrazada? Las preguntas que repartió en el congreso estaban relacionadas con esta hipótesis.
La idea de que cada forma modular estuviera asociada a una ecuación elíptica era tan extraordinaria que los que echaron un vistazo a las cuestiones de Taniyama las trataron nada más que como una curiosa observación. Sin duda, Taniyama había demostrado que unas cuantas ecuaciones elípticas podían asociarse con formas modulares particulares, pero afirmaban que esto no era más que una coincidencia. De acuerdo con los escépticos, la afirmación de Taniyama de una relación más general y universal parecía estar muy poco corroborada. La hipótesis estaba basada en la intuición más que en evidencias reales.
El único aliado de Taniyama fue Shimura, que creía en el poder y la profundidad de la idea de su amigo. Tras el simposio trabajó con Taniyama en un intento de desarrollar la hipótesis hasta un nivel en el que el resto del mundo no pudiera ignorar su trabajo. Shimura quería encontrar más evidencias para respaldar la relación entre los mundos modular y elíptico. La colaboración se interrumpió temporalmente cuando en 1957 Shimura fue invitado a trabajar en el Institute for Advanced Estudy de Princeton. Tras dos años como profesor invitado en Estados Unidos planeaba retomar el trabajo con Taniyama, pero eso nunca ocurrió. El 17 de noviembre de 1957 Yutaka Taniyama se suicidó.
La muerte de un genio
Shimura aún conserva la carta que Taniyama le envió cuando tuvieron su primer contacto acerca del libro de la biblioteca. También conserva la última carta que Taniyama le escribió mientras él estaba en Princeton, pero ésta no contiene la más mínima indicación sobre lo que ocurriría dos meses después. Hasta hoy, Shimura no comprende cuál fue la causa del suicidio de Taniyama. «Yo estaba muy confundido. Confusión puede ser la mejor palabra. Por supuesto estaba triste, pero fue tan repentino. Recibí esta carta en septiembre y él murió a principios de noviembre, y no pude encontrar el sentido a todo esto. Luego oí varias cosas y traté de hacerme a la idea de su muerte. Algunos dijeron que había perdido la confianza en sí mismo, pero no en sus capacidades matemáticas».
Particularmente desconcertante para los amigos de Taniyama fue que se había enamorado de Misako Suzuki y planeaban casarse aquel mismo año. Como un tributo personal publicado en el Bulletin of the London Mathematical Society, Goro Shimura recuerda el compromiso de Taniyama con Misako y las semanas que precedieron al suicidio:
Cuando me informaron de su compromiso me sorprendí un poco, porque me parecía que ella no era su tipo, pero no sentí recelos. Más tarde me dijeron que habían firmado el contrato de alquiler de un apartamento, al parecer mejor, para convertirlo en su nuevo hogar, habían comprado cacharros de cocina juntos y se estaban preparando para la boda. A ellos y sus amigos todo les parecía muy halagüeño. Entonces la catástrofe les cayó encima.
En la mañana del lunes 17 de noviembre de 1958, el vigilante de su apartamento lo encontró muerto en su habitación con una nota sobre la mesa. Estaba escrita en tres páginas de una libreta del mismo tipo que había usado para su trabajo de investigación; el primer párrafo decía:
«Hasta ayer no tenía una intención clara de matarme. Pero bastantes personas deben de haberse dado cuenta de que últimamente he estado cansado tanto física como mentalmente. Ni yo mismo entiendo del todo la causa de mi suicidio, pero no es el resultado de ningún incidente en particular ni de nada específico. Simplemente puedo decir que estoy en un estado de ánimo tal que he perdido la confianza en mi futuro. Puede haber alguien para quien mi suicidio sea inquietante o, hasta cierto punto, un golpe. Sinceramente espero que este incidente no proyecte ninguna sombra sobre el futuro de esa persona. De ninguna manera puedo negar que esto no sea una forma de traición, pero, por favor, excusadlo como mi último acto, que he hecho a mi manera, igual que siempre he ido por libre toda la vida».
Seguía describiendo, de forma bastante metódica, sus deseos sobre cómo efectuar el reparto de sus bienes y qué libros y discos había tomado prestados de la biblioteca o de sus amigos, y así sucesivamente. Específicamente dice: «Me gustaría dejar mis discos y el tocadiscos a Misako Suzuki, suponiendo que no esté enfadada conmigo por dejárselos». También explica hasta dónde había llegado en los cursos de cálculo y álgebra lineal que estaba dando, y concluye la nota con una disculpa a sus colegas por los inconvenientes que su acto pudiera causar.
Así, una de las mentes más brillantes y avanzadas de su tiempo finalizó su vida por propio deseo. Había cumplido treinta y un años cinco días antes.
Unas cuantas semanas después del suicidio la tragedia golpeó por segunda vez. Su prometida, Misako Suzuki, también se quitó la vida. Según se dice, dejó una nota en la que se leía: «Nos prometimos mutuamente que, sin importar adonde fuéramos, nunca nos separaríamos. Ahora que él se ha ido yo debo ir también para reunirme con él».
La filosofía de la bondad
Durante su corta carrera, Taniyama contribuyó a las matemáticas con varias ideas radicalmente nuevas. Las preguntas que repartió en el simposio contenían su mayor intuición, pero estaban tan adelantadas a su tiempo que nunca vivió para ver la enorme influencia que tuvieron en la teoría de números. Su creatividad intelectual fue tristemente echada de menos, al igual que su papel de guía dentro de la comunidad de jóvenes científicos japoneses. Shimura recuerda con claridad la influencia de Taniyama: «Siempre era amable con sus colegas, especialmente con sus estudiantes jóvenes, y se preocupaba de manera sincera por su bienestar. Fue el apoyo moral de muchos de los que entraron en contacto matemático con él, incluyéndome por supuesto a mí mismo. Probablemente nunca fue consciente del papel que estaba desempeñando. Pero ahora noto su noble generosidad a este respecto más que cuando estaba vivo. Y sin embargo, nadie pudo darle ningún apoyo cuando lo necesitó desesperadamente. Cuando pienso en ello me abruma la pena más amarga».
Tras la muerte de Taniyama, Shimura concentró todos sus esfuerzos en comprender la relación exacta entre las ecuaciones elípticas y las formas modulares. Con el paso de los años se esforzó para obtener alguna evidencia más y uno o dos argumentos lógicos para sostener la teoría. Gradualmente se fue convenciendo de que cada ecuación elíptica estaba relacionada con una forma modular. Otros matemáticos aún mantenían dudas y Shimura recuerda una conversación con un eminente colega. El profesor preguntó: «He oído que usted propone que algunas ecuaciones elípticas se pueden conectar con formas modulares».
«No, no lo ha entendido —replicó Shimura—. No son sólo algunas ecuaciones elípticas, son todas las ecuaciones elípticas».
Shimura no pudo demostrar que esto era cierto, pero cada vez que ponía a prueba la hipótesis parecía ser verdadera, y en cualquier caso en conjunto parecía encajar en su filosofía general de las matemáticas. «Yo tengo la filosofía de la bondad. Las matemáticas deben contener bondad. Así, en el caso de las ecuaciones elípticas, se podría llamar buena a la ecuación si estuviera parametrizada por una forma modular. Yo espero que todas las ecuaciones elípticas sean buenas. Es una filosofía un poco rudimentaria pero siempre se puede tomar como punto de partida. Entonces, por supuesto, tenía que desarrollar varias razones técnicas para la conjetura. Debería decir que la conjetura surgía de la filosofía de la bondad. La mayor parte de los matemáticos hacen matemáticas desde un punto de vista estético, y esta filosofía de la bondad proviene de mi punto de vista estético».
Con el tiempo, la acumulación de evidencias por Shimura significó que su teoría acerca de las ecuaciones elípticas y las formas modulares se hiciera ampliamente aceptada. No pudo demostrar al resto del mundo que tenía razón, pero por lo menos ya no eran meras ilusiones. Existían suficientes evidencias como para que mereciera el título de conjetura. Al principio fue conocida como la conjetura de Taniyama-Shimura en reconocimiento del hombre que la inspiró a su colega y de éste, que prosiguió el trabajo hasta desarrollarla completamente.
En su momento, André Weil, uno de los padrinos de la teoría de números del siglo XX, adoptó la conjetura y le dio publicidad en Occidente. Weil investigó la idea de Shimura y Taniyama y encontró aún más evidencias a su favor. Como resultado, la conjetura se denomina frecuentemente la conjetura de Taniyama-Shimura-Weil, a veces la conjetura de Taniyama-Weil y en ocasiones como la conjetura de Weil. De hecho ha habido mucho debate y controversia sobre el nombre oficial de la conjetura. Para aquellos que estén interesados en la combinatoria existen quince permutaciones posibles de los tres nombres involucrados y es posible que cada una de ellas haya aparecido impresa a lo largo de los años. Sin embargo, yo me referiré a la conjetura por su nombre original: la conjetura de Taniyama-Shimura.
El profesor John Coates, que dirigió a Andrew Wiles cuando era un estudiante, era a su vez un estudiante cuando la conjetura de Taniyama-Shimura se convirtió en un tema de conversación en Occidente. «Empecé a investigar en 1966, cuando la conjetura de Taniyama y Shimura estaba extendiéndose por el mundo. Todos estaban asombrados y empezaron a ocuparse seriamente de si todas las ecuaciones elípticas podían ser modulares. Fue un tiempo tremendamente emocionante; el único problema, por supuesto, fue que parecía muy difícil hacer progresos. Creo que es justo decir que, por bella que fuera esta idea, parecía muy difícil de demostrar, y esto es lo que interesa sobre todo a los matemáticos».
Durante el final de los sesenta, una legión de matemáticos comprobó repetidamente la conjetura de Taniyama-Shimura. Partiendo de una ecuación elíptica y su serie E, buscaban una forma modular con una serie M idéntica. En todos los casos, la ecuación elíptica tenía asociada una forma modular. Aunque esto era una buena evidencia en favor de la conjetura de Taniyama-Shimura, no era en absoluto una prueba. Los matemáticos sospechaban que era cierta, pero hasta que alguien encontrara una demostración lógica continuaría siendo una mera conjetura.
Barry Mazur, un profesor de la Universidad de Harvard, fue testigo de la ascensión de la conjetura de Taniyama-Shimura. «La suposición de que cada ecuación elíptica estaba asociada a una forma modular era una bella conjetura, pero al principio fue ignorada por estar demasiado adelantada a su tiempo. Cuando se propuso por primera vez no fue considerada debido a que era demasiado asombrosa. Por un lado se tiene el mundo elíptico, y en el otro se tiene el mundo modular. Las dos ramas de las matemáticas se habían estudiado de forma intensa pero separada. Los matemáticos que estudiaban las ecuaciones elípticas podían no estar bien preparados en formas modulares, y viceversa. Entonces llega la conjetura de Taniyama-Shimura, la gran suposición de que existe un puente entre esos dos mundos completamente diferentes. A los matemáticos les encanta construir puentes».
El valor de los puentes matemáticos es enorme. Permiten intercambiar ideas a comunidades matemáticas que habían estado viviendo en islas separadas y explorar mutuamente sus creaciones. Las matemáticas consisten en islas de conocimiento dentro de un mar de ignorancia. Por ejemplo, existe una isla ocupada por los geómetras que estudian las formas y las figuras, y existe una isla de la probabilidad en la que los matemáticos discuten sobre el riesgo y la posibilidad. Hay docenas de estas islas, cada una con su lenguaje propio y único, incomprensible para los habitantes de otras islas. El lenguaje de la geometría es muy diferente del lenguaje de la probabilidad, y la jerga del cálculo no tiene sentido para aquellos que sólo hablan de estadística.
El gran potencial de la conjetura de Taniyama-Shimura era que conectaría dos islas y permitiría a sus habitantes hablar entre ellos por primera vez. Barry Mazur considera la conjetura de Taniyama-Shimura un instrumento de traducción tal como la piedra de Rosetta, que contenía textos en demótico egipcio, griego antiguo y jeroglíficos. Puesto que se comprendía el demótico y el griego, los arqueólogos pudieron descifrar los jeroglíficos por primera vez. «Es como si entendieras un lenguaje y esta piedra de Rosetta te proporcionara un conocimiento profundo del otro idioma —dice Mazur—. Pero la conjetura de Taniyama-Shimura es una piedra de Rosetta con un cierto poder mágico. La conjetura tiene la encantadora propiedad de que simples intuiciones en el mundo modular se traducen en profundas verdades en el mundo elíptico, y viceversa. Es más, profundos problemas del mundo elíptico pueden resolverse a veces traduciéndolos por medio de esta piedra de Rosetta al mundo modular y descubriendo que tenemos intuiciones y herramientas en el mundo modular para tratar el problema traducido. En el mundo elíptico habríamos estado perdidos».
Si la conjetura de Taniyama-Shimura fuera cierta, permitiría a los matemáticos abordar problemas elípticos que habían permanecido sin resolver durante siglos por medio de un acercamiento a través del mundo modular. La esperanza era que los mundos elíptico y modular pudieran ser unificados. La conjetura también constituyó la esperanza de que pudieran existir nexos entre otros varios campos matemáticos.
Durante los años sesenta, Robert Langlands, que trabajaba en el Institute for Advanced Estudy de Princeton, quedó impresionado por la potencia de la conjetura de Taniyama-Shimura. Incluso aunque la conjetura aún no había sido demostrada, Langlands creía que era sólo un elemento de un esquema mucho mayor de unificación. Confiaba en que existieran nexos entre las principales áreas de las matemáticas y se puso a buscar esas unificaciones. En unos pocos años empezaron a aparecer los nexos. Todas esas otras conjeturas de unificación eran mucho más débiles y especulativas que la de Taniyama-Shimura, pero formaban una intrincada red de conexiones hipotéticas entre varias áreas de las matemáticas. El sueño de Langlands era ver cada una de esas conjeturas demostradas una por una y que ello llevara a una gran unificación de las matemáticas.
Langlands comentó su plan para el futuro e intentó convencer a otros matemáticos para que tomaran parte en lo que se llegó a conocer como el Programa Langlands, un esfuerzo concentrado en demostrar su miríada de conjeturas. Parecía no haber un medio obvio para demostrar esos nexos especulativos, pero si el sueño se pudiera hacer realidad entonces la recompensa sería enorme, cualquier problema insoluble en una área de las matemáticas se podría transformar en un problema análogo en otra área en la cual se podría usar un nuevo arsenal de técnicas para luchar con él. Si la solución aún fuera elusiva, el problema podría ser transformado y transportado a una nueva área de las matemáticas, y así sucesivamente hasta que fuera resuelto. Un día, de acuerdo con el Programa Langlands, los matemáticos serían capaces de resolver sus problemas más oscuros e intratables transportándolos a lo largo del panorama matemático.
Había también grandes implicaciones en las ciencias aplicadas y la ingeniería. Tanto cuando se modelan las interacciones entre quarks en colisión como cuando se buscan las maneras más eficientes de organizar una red de telecomunicaciones, a menudo la clave del problema está en realizar algún cálculo matemático. En algunas áreas de la ciencia y la tecnología, la complejidad de los cálculos es tan inmensa que el progreso en esos temas se ve muy dificultado. Si los matemáticos pudieran probar las conjeturas de unión del Programa Langlands, habría atajos para resolver problemas del mundo real, así como los del abstracto.
En la década de los setenta, el Programa Langlands se había convertido en el plan maestro del futuro de las matemáticas, pero su camino hasta el paraíso de los expertos en la resolución de Problemas estaba bloqueado por el simple hecho de que nadie tenía ninguna idea sobre cómo probar algunas de las conjeturas del Programa Langlands. La conjetura más fuerte en el programa aún era la de Taniyama-Shimura, pero incluso ésta parecía fuera de alcance. Una demostración de la conjetura de Taniyama-Shimura sería el primer paso en el programa Langlands, y como tal se había convertido en uno de los mayores premios de la teoría de números moderna.
A pesar de su condición de conjetura sin demostrar, la de Taniyama-Shimura se citaba en cientos de artículos matemáticos en los que se especulaba sobre lo que sucedería si se pudiera demostrar. Los artículos empezaban enunciando claramente la advertencia «Asumiendo que la conjetura de Taniyama-Shimura es cierta…», y entonces continuaban describiendo una solución al problema sin resolver. Por supuesto, estos resultados dependían de la certeza de la conjetura de Taniyama-Shimura. Estos nuevos resultados hipotéticos fueron a su vez incorporados en otros resultados, hasta que existió una plétora de matemáticas que dependía de la certeza de la conjetura de Taniyama-Shimura. Esta conjetura constituyó los cimientos de una arquitectura completamente nueva de las matemáticas pero, hasta que se pudiera demostrar, toda esta estructura era vulnerable.
En aquel tiempo, Andrew Wiles era un joven investigador en la Universidad de Cambridge, y recuerda la agitación que sufría la comunidad matemática en los setenta: «Construimos más y más conjeturas que se extendían más y más allá en el futuro, pero que serían ridículas si la conjetura de Taniyama-Shimura no fuera correcta. Por lo tanto, debíamos probar la de Taniyama-Shimura para mostrar que el diseño completo que habíamos trazado esperanzadamente para el futuro era correcto».
Los matemáticos habían construido un frágil castillo de naipes. Soñaban con que alguien le daría algún día los sólidos cimientos que precisaba su arquitectura. También debían vivir con la pesadilla de que alguien probara en cualquier momento que en realidad la conjetura de Taniyama-Shimura era errónea, lo que provocaría la caída de dos décadas de investigación.
El nexo perdido
Durante el otoño de 1984, un grupo selecto de teóricos de números asistió a un simposio en Oberwolfach, una pequeña ciudad en el corazón de la Selva Negra, en Alemania. Se habían reunido para discutir varios importantes avances en el estudio de las ecuaciones elípticas y, naturalmente, algunos de los conferenciantes informarían ocasionalmente sobre algún pequeño progreso que hubieran realizado para probar la conjetura de Taniyama-Shimura. Uno de los conferenciantes, Gerhard Frey, un matemático de Saarbruck, no podía ofrecer ninguna idea nueva sobre cómo atacar la conjetura, pero hizo la sorprendente afirmación de que, si alguien conseguía demostrarla, podría probar de manera inmediata el último teorema de Fermat.
Cuando Frey se levantó para dar su charla, empezó escribiendo la ecuación de Fermat:
xn + yn = zn, donde n es mayor que 2.
El último teorema de Fermat asegura que no hay soluciones formadas por números enteros para la ecuación anterior, pero Frey exploró qué sucedería si el último teorema fuera falso, es decir, que existiera al menos una solución entera. Frey no sabía cuál era su hipotética, y herética, solución, y por ello etiquetó los números desconocidos con las letras A, B y C:
An + Bn = Cn,
Frey procedió a «reordenar» la solución. Este es un procedimiento matemático riguroso que cambia el aspecto de la ecuación sin alterar su integridad. Por medio de una hábil serie de complicadas maniobras, Frey transformó la ecuación original de Fermat, con su hipotética solución, en
y2 = x3 + (An − Bn) x2 − AnBn.
Aunque esta disposición parece muy distinta de la ecuación original es una consecuencia directa de la solución hipotética. Es decir, que si, y éste es una gran «si», existe una solución a la ecuación de Fermat y el último teorema es falso, entonces esta ecuación refundida también debe existir. Inicialmente, el público de Frey no estaba particularmente impresionado por su nueva expresión, pero entonces hizo notar que esta nueva ecuación es de hecho una ecuación elíptica, aunque bastante complicada y exótica. Las ecuaciones elípticas tienen la forma
y2 = x3 + ax2 + bx + c,
y si se hacen las identificaciones
a = An − Bn, b = 0, c = −AnBn.
entonces es más fácil apreciar la naturaleza elíptica de la ecuación de Frey.
Al transformar la ecuación de Fermat en una ecuación elíptica, Frey había unido el último teorema de Fermat con la conjetura de Taniyama-Shimura. Frey mostró a la audiencia que su ecuación elíptica, creada a partir de la solución a la ecuación de Fermat, era realmente extraña. De hecho, Frey proclamó que su ecuación elíptica es tan rara que las repercusiones de su existencia serían devastadoras para la conjetura de Taniyama-Shimura.
Pero recuérdese que la ecuación elíptica de Frey es sólo una ecuación fantasma. Su existencia está condicionada al hecho de que el último teorema de Fermat sea falso. Sin embargo, si la ecuación elíptica de Frey existe entonces es tan extraña que parecería imposible relacionarla nunca con una forma modular. Pero la conjetura de Taniyama-Shimura afirma que cada ecuación elíptica debe estar relacionada con una forma modular. Por lo tanto, la existencia de la ecuación elíptica de Frey desafía a la conjetura de Taniyama-Shimura.
En otras palabras, el argumento de Frey es como sigue:
- Si (y sólo si) el último teorema de Fermat es erróneo, entonces existe la ecuación elíptica de Frey.
- La ecuación elíptica de Frey es tan extraña que de ninguna manera puede ser modular.
- La conjetura de Taniyama-Shimura asegura que cada ecuación elíptica debe ser modular.
- ¡En consecuencia, la conjetura de Taniyama-Shimura debe ser falsa!
De forma alternativa, y aún más importante, Frey podía enunciar su argumento al revés:
- Si la conjetura de Taniyama-Shimura se puede demostrar cierta, entonces cada ecuación elíptica tiene que ser modular.
- Si cada ecuación elíptica es modular, entonces está prohibida la existencia de la ecuación elíptica de Frey.
- Si la ecuación elíptica de Frey no existe, entonces no puede haber solución a la ecuación de Fermat.
- ¡Entonces el último teorema de Fermat es cierto!
Gerhard Frey había llegado a la sensacional conclusión de que la certeza del último teorema de Fermat debería ser una consecuencia inmediata de la demostración de la conjetura de Taniyama-Shimura. Frey afirmaba que si los matemáticos pudieran demostrar la conjetura, entonces probarían automáticamente el último teorema de Fermat. Por primera vez en un siglo el problema más complicado de las matemáticas parecía vulnerable. De acuerdo con Frey, demostrar la conjetura de Taniyama-Shimura era el único obstáculo que se debía vencer para probar el último teorema de Fermat.
Aunque la audiencia estaba impresionada por la brillante intuición de Frey, también estaba sorprendida por un error elemental de su razonamiento. Casi todo el mundo entre los asistentes lo había detectado, salvo el mismo Frey. El error no parecía grave, pero, sin embargo, el trabajo de Frey estaba incompleto. Quienquiera que fuera el primero en corregir el error recibiría el crédito de haber relacionado Fermat y Taniyama-Shimura.
El público de Frey salió precipitadamente del auditorio y se dirigió a la sala de la fotocopiadora. A menudo, la importancia de una charla se puede medir por la longitud de la cola que espera para hacer copias de la conferencia. Con el esbozo completo de las ideas de Frey, volvieron a sus respectivas instituciones e intentaron rellenar la brecha.
El argumento de Frey dependía del hecho de que su ecuación elíptica era tan extraña que no podía ser modular. Su trabajo estaba incompleto debido a que no había demostrado en absoluto que su ecuación elíptica fuera suficientemente extraña. Sólo cuando se pudiera probar la absoluta extrañeza de la ecuación elíptica de Frey la demostración de la conjetura de Taniyama-Shimura implicaría la demostración del último teorema de Fermat.
Al principio, los matemáticos creyeron que demostrar la extrañeza de la ecuación elíptica de Frey sería un proceso bastante rutinario. A primera vista, el error de Frey parecía elemental y cualquiera de los que acudieron a Oberwolfach creyó que aquello iba a ser una carrera para ver quién podía realizar antes los cálculos. Se esperaba que alguien enviaría un mensaje por correo electrónico en cuestión de días para demostrar cómo había establecido la verdadera extrañeza de la ecuación elíptica de Frey.
Pasó una semana sin que el mensaje llegara. Pasaron meses, y lo que se creyó que iba a ser una loca carrera matemática se transformó en una maratón. Parecía que Fermat aún estaba tomando el pelo y atormentando a sus descendientes. Frey había diseñado una estrategia sugestiva para probar el último teorema de Fermat, pero incluso el primer paso elemental, demostrar que la ecuación elíptica de Frey no era modular, era desconcertante para los matemáticos del mundo entero.
Para demostrar que la ecuación elíptica no era modular, los matemáticos buscaban invariantes similares a los descritos en el capítulo 4. El invariante del nudo mostraba que un nudo no se podía transformar en otro, y el invariante del puzzle de Loyd mostraba que su «rompecabezas 14 15» no se podía disponer en la ordenación correcta. Si los teóricos de números pudieran descubrir un invariante apropiado para describir la ecuación elíptica de Frey, entonces podrían probar que, sin importar cómo se transformara, nunca podría convertirse en una forma modular.
Uno de los que trabajaban afanosamente buscando la demostración que completaría la conexión entre la conjetura de Taniyama-Shimura y el último teorema de Fermat era Ken Ribet, un profesor de la Universidad de California en Berkeley. Desde la conferencia en Oberwolfach, Ribet se había obsesionado con demostrar que la ecuación elíptica de Frey era demasiado extraña para ser modular. Tras dieciocho meses de esfuerzo, él, junto con algunos más, no estaba llegando a ninguna parte. Entonces, en el verano de 1986 el colega de Ribet, Barry Mazur, estuvo de visita en Berkeley para asistir al Congreso Internacional de Matemáticas. Los dos amigos se encontraron para tomar un capuchino en el café Strada y empezaron a compartir sus historias de mala suerte y refunfuñar acerca del estado de las matemáticas.
Al final hablaron de las últimas noticias sobre los varios intentos de demostrar la extrañeza de la ecuación elíptica de Frey, y Ribet explicó un ensayo estrategia que había estado explorando. El enfoque que parecía vagamente prometedor, pero sólo podía demostrar una parte pequeña del mismo. «Me senté con Barry y le conté en qué estaba trabajando. Mencioné que había demostrado un caso muy especial, pero que no sabía qué hacer ahora para generalizarlo y obtener toda la fuerza de la demostración».
El profesor Mazur sorbía su capuchino y escuchaba la idea de Ribet. Entonces se detuvo y miró incrédulo a Ribet. «¿Pero no lo ves? ¡Ya lo has hecho! Todo lo que tienes que hacer es añadir alguna estructura gamma-cero de (M), volver a enunciar todo tu argumento, y ya está. Te da todo lo que necesitas».
Ribet miró a Mazur, miró su capuchino y volvió a mirar a Mazur. Ése era el momento más importante en la carrera de Ribet y lo recuerda con todo detalle. «Yo dije que tenía toda la razón, por supuesto, cómo pude no verlo. Estaba completamente estupefacto porque nunca se me había ocurrido añadir la estructura gamma-cero de (M) adicional, tan simple como suena».
Hay que hacer notar que, aunque añadir la estructura gamma-cero de (M) le pareciera muy simple a Ken Ribet, es en realidad un complicado paso lógico que tan sólo un puñado de matemáticos del mundo podrían haber fraguado mientras tomaban un capuchino.
«Éste era el ingrediente crucial que necesitaba y lo había tenido ante mis narices. Volví a mi apartamento como en una nube, pensando: Dios mío, ¿será esto realmente correcto? Estaba extasiado; me senté y empecé a garabatear en una libreta. Tras una o dos horas lo había escrito todo y verificado los pasos clave, y todo encajaba. Rehíce por completo mi argumento y me dije: Sí, esto tiene que funcionar. Y, por supuesto, ahí estaban varios miles de matemáticos en el Congreso Internacional y, de forma más o menos casual, comenté a unas cuantas personas que había demostrado que la conjetura de Taniyama-Shimura implica el ultimo teorema de Fermat. La noticia se propagó como el fuego y pronto grandes grupos lo sabían; venían corriendo a mí y me preguntaban: “¿Es realmente cierto que has demostrado que la ecuación elíptica de Frey no es modular?”. Y, tras meditar durante un minuto, de repente dije: “Sí, lo he hecho”».
Ahora el último teorema de Fermat estaba inextricablemente unido a la conjetura de Taniyama-Shimura. Si alguien podía demostrar que todas las ecuaciones elípticas son modulares, eso implicaría que la ecuación de Fermat no tiene soluciones y, de forma inmediata, demostraría el último teorema de Fermat.
Durante tres siglos y medio, el último teorema de Fermat había sido un problema aislado, un curioso e imposible enigma en el último confín de las matemáticas. Ahora Ken Ribet, inspirado por Gerhard Frey, lo había llevado al centro de la escena. El problema más importante del siglo XVII estaba unido al problema más significativo del siglo XX. Un enigma de una enorme importancia histórica y emocional estaba asociado a una conjetura que podía revolucionar las matemáticas modernas.
Frey había definido claramente la tarea que había por delante. Los matemáticos demostrarían automáticamente el último teorema de Fermat si eran capaces de probar primero la conjetura de Taniyama-Shimura. Al principio hubo una renovada esperanza, pero entonces se empezó a comprender la realidad de la situación. Los matemáticos habían intentado demostrar la realidad de la conjetura de Taniyama-Shimura durante treinta años y habían fallado. ¿Por qué iban a avanzar ahora? Los escépticos opinaban que cualquier pequeña esperanza de demostrar la conjetura se había desvanecido. Su argumento era que cualquier cosa que pudiera llevar a una solución del último teorema de Fermat debía ser, por definición, imposible.
Incluso Ken Ribet, que había realizado el avance crucial, era pesimista: «Yo era uno más de la vasta mayoría que creía que la conjetura de Taniyama-Shimura era completamente inaccesible. Ni siquiera me preocupé en intentar demostrarla. Ni siquiera me pasó por la cabeza. Andrew Wiles fue probablemente una de las pocas personas en la Tierra que tuvo la audacia de soñar que se podía poner a ello y demostrar la conjetura».