Notas matemáticas

^[M1] Ésta no es realmente una nota matemática, pero el bebé del sábado por la noche es tridimensional [figura A1].

FIGURA A1. Bebé del sábado por la noche.

<<

^[M2] Una métrica en un espacio puede tomar la forma ds² Una métrica en un espacio puede tomar la forma ds² = a_xdx² + a_ydy² + a_zdz², donde x, y, z son las tres coordenadas del espacio y a_x, a_y, a_z pueden ser números o pueden ser funciones de x, y y z. La métrica determina las longitudes, las distancias y los ángulos entre líneas. Por ejemplo, la longitud de un vector que sale del origen y va hasta el punto de coordenadas (x, y, z) es Si a_x = a_y = a_z = 1, tenemos el espacio plano, y las distancias y las longitudes se medirían de la manera familiar. Por ejemplo, la longitud de un vector que sale del origen y va hasta (x, y, z) sería Hay métricas más complicadas que tienen términos cruzados, como dxdy. En ese caso, la métrica hay que describirla con un tensor con dos índices que dice los coeficientes a_ij de cada término de la forma dx_idx_j en la métrica. Más tarde, cuando discutamos la relatividad, la métrica tendrá también un término dt² y podría también tener términos de la forma dtdx_i. <<

^[M3] Una hiperesfera se define por medio de la ecuación Aquí x_i se refiere a la coordenada que ocupa el lugar i (la localización en la dimensión i) y r es el radio de la hiperesfera. La sección de la hiperesfera cuando cruza una localización fija en la dimensión n, x_n = d, está descrita por la ecuación Ésta es la ecuación de una hiperesfera de una dimensión menos y radio Así, por ejemplo, cuando n = 3 y una esfera cruza Planilandia, los habitantes de Planilandia verán círculos. (Verían discos si ven los círculos y sus interiores, lo que matemáticamente se describiría con una desigualdad). <<

^[M4] Las variedades de Calabi-Yau no son las únicas variedades que las cuerdas ocultan. Sabemos ahora que hay otras, como las llamadas variedades de holonomía G2, que podrían proporcionar también modelos aceptables. <<

^[M5] En la teoría de cuerdas, también usamos a veces la palabra brana para denominar a las branas que ocupan todo el espacio y que tienen el mismo número de dimensiones que el espacio de dimensión superior. Aquí, sin embargo, nos ocuparemos solamente de las branas que tienen menos dimensiones que el espacio completo de dimensión superior, de modo que me limitaré a usar el término en el sentido descrito en el texto. <<

^[M6] Una brana que se extiende en las dimensiones x1, …, x_j está descrita por las n – j ecuaciones x_j+1 = c_j+1, x_j+2 = c_j+2, …, x_n = c_n, donde las x_i son coordenadas, n es el número de dimensiones del espacio y las c_i son constantes fijas que describen la localización de la brana. Las branas más complicadas que se curvan en el sistema coordenado dado se describen con ecuaciones más complicadas que describen la superficie. <<

^[M7] En forma de ecuación, la ley de Newton dice que la fuerza gravitatoria es Gm₁m₂/r², donde G es la constante de la gravitación de Newton, m₁ y m₂ son las dos masas que se atraen entre sí y r es la distancia entre ellas. <<

^[M8] La gravedad newtoniana respeta la geometría de Euclides. En la geometría euclídea, x² + y² + z², la longitud de un vector que parte del origen y acaba en el punto de coordenadas (x, y, z) es independiente del sistema coordenado. Esto es, uno puede rotar las coordenadas pero la distancia a cualquier punto no cambiará, aunque sí que cambian las coordenadas individuales. La relatividad especial introduce el tiempo en esta descripción. Dice que x² + y² + z² – c²t² es independiente de la elección de sistema de referencia inercial. Obsérvese que, esta cantidad invariante involucra tanto el espacio como el tiempo, pero el tiempo recibe un trato diferente a causa del signo menos que lleva el término c²t². Obsérvese también que, para que esta cantidad sea independiente del sistema de referencia inercial, los cambios de sistema de referencia han de mezclar los valores de las coordenadas del espacio y del tiempo. Si un sistema de referencia se mueve a una velocidad v con respecto al otro en la dirección x, la transformación de coordenadas de (t, x, y, z) a (t’, x’, y’, z’) sería y’ = y, z’ = z, donde c es la velocidad de la luz y <<

^[M9] Las ecuaciones de Einstein nos dicen cómo deducir la métrica g_μν a partir de una distribución dada de materia y energía:

R_μν es el tensor de curvatura de Ricci y está relacionado con la métrica g_μν, T_μν es el tensor de tensión-energía que describe la distribución de materia y energía, G es la constante de gravitación de Newton y c es la velocidad de la luz. Por ejemplo, para materia con densidad de masa ρ en reposo, T₀₀ = ρ mientras todos los demás componentes del tensor son 0. <<

^[M10] La energía por unidad de frecuencia emitida por un cuerpo negro de temperatura T depende de la frecuencia f según la fórmula f³/(e^hf/kT–1), donde k = 1,3807 × 10^–6 ergios/K es la constante de Boltzmann, que convierte la temperatura en energía. Obsérvese que a bajas frecuencias la energía aumenta con la frecuencia. Pero a frecuencias en las que la energía de un cuanto, hf, es grande comparada con kT, el espectro cae drásticamente; la energía emitida es exponencialmente más pequeña a frecuencias más altas. <<

^[M11] Una función de onda es realmente una función que toma valores complejos. Ésta es la fuente de muchas de las propiedades extrañas de la mecánica cuántica. Cuando sumamos dos funciones complejas y elevamos al cuadrado la suma, generalmente obtenemos un resultado distinto del que obtenemos cuando primero elevamos al cuadrado y luego sumamos. Esto trae como consecuencia fenómenos de interferencia. Por ejemplo, en el experimento de la doble rendija, la probabilidad que queda registrada en una pantalla resulta de la interferencia de las ondas que describen los dos posibles caminos del electrón. <<

^[M12] Más precisamente, es el producto de la constante de Planck y el valor absoluto del conmutador de las dos cantidades dividido por 2. <<

^[M13] La relatividad especial nos dice que un objeto estacionario con masa en reposo m0 porta una energía E = m₀c². Más generalmente, un objeto que se mueve con velocidad v (con y ) portará una energía E = γm₀c². La masa en reposo se conoce también como masa invariante (independiente del sistema de referencia). Esto es así porque, según las leyes de transformación de la relatividad especial, la cantidad E² – p²c² = m₀c⁴ es la misma en cualquier sistema de referencia. Obsérvese que siempre se precisa una energía al menos igual a m₀c² para producir un objeto con masa m₀. Obsérvese también que cuando un objeto tiene una masa pequeña comparada con su energía (realmente energía/c²), la energía y el momento están relacionadas de forma aproximada por E = pc. Esta es la razón por la cual la energía y el momento son más o menos intercambiables. <<

^[M14] Las ecuaciones de Maxwell son (en unidades c.g.s.) donde E es el campo eléctrico, B es el campo magnético, ρ es la carga y J es la corriente. Éstas son ecuaciones diferenciales de primer orden; combinando dos de ellas podemos deducir una ecuación diferencial de segundo orden que involucra solamente el campo eléctrico o el campo magnético. Esta ecuación asume la forma de una ecuación de onda, esto es, sus soluciones son ondas sinusoidales.

<<

^[M15] Realmente, según los principios subyacentes de la relatividad especial, podría haber habido también una cuarta polarización, que oscilaría en la dirección del tiempo. Pero ésta no existe en todo caso, ya que la misma simetría interna que elimina la tercera polarización (longitudinal) elimina también la «polarización temporal». Como no desempeña ningún papel en la discusión de este capítulo ni en la del siguiente, ya no hablaremos más de ella. <<

^[M16] Las auténticas simetrías asociadas con todas las fuerzas son, de hecho, más sutiles y rotan los campos entre sí, los cuales son cantidades complejas. Las simetrías no intercambian simplemente los campos, sino que convierten un campo en una superposición lineal de los otros. La fuerza asociada con el electromagnetismo rota un único campo complejo, mientras que la fuerza débil rota dos campos complejos entre sí, y la fuerza fuerte rota tres. <<

^[M17] Para hacer que funcione un modelo de Higgs, al menos uno de los campos de Higgs ha de estar forzado a tomar un valor no nulo. Esto sería cierto si la configuración de energía mínima se da cuando el valor de al menos uno de los campos de Higgs es no nulo. Una manera en que esto puede ocurrir se ilustra en la figura A2, que muestra lo que se llama el potencial del sombrero mexicano, una representación gráfica de la energía que tomaría el sistema para cualquier combinación de valores de los dos campos de Higgs, donde los dos ejes inferiores son los valores absolutos de los dos campos de Higgs y la altura de la superficie tridimensional representa la energía de esa configuración concreta. Este potencial concreto toma la forma donde λ determina cuán abombado es el potencial y v determina el valor que tomará cuando el potencial sea mínimo. La propiedad clave de este potencial es que, cuando ambos campos tienen valor cero, esto se da en un máximo local. Por lo tanto, consideraciones sobre la energía nos dicen que los campos de Higgs no serán ambos cero. Por el contrario, tomarán valores que los coloquen en el fondo del cuenco circular que rodea el origen.

FIGURA A2. El potencial del «sombrero mexicano» para el campo de Higgs.

<<

^[M18] Una manera más precisa de describir la simetría de la fuerza débil sería decir que rota los campos, más que intercambiarlos. <<

^[M19] Esto simplifica, de hecho, la ruptura de la simetría. Incluso si x e y fueran ambos no nulos —por ejemplo, si x e y fueran ambos 5— la simetría rotacional se rompería ya que se elige una dirección particular, la dirección que apunta desde x = 0, y = 0 al punto donde x = 5, y = 5. Una simetría «rotacional» análoga se aplica a Higgs₁ y Higgs₂, pero he simplificado y descrito la simetría sencillamente como una simetría de intercambio. En la descripción auténtica, incluso si ambos campos de Higgs toman el mismo valor, la simetría de la interacción débil se rompería, de un modo muy parecido a lo que ocurre cuando el punto x = 5, y = 5 rompe espontáneamente la simetría rotacional. <<

^[M20] Aunque este modelo arranca con dos campos complejos de Higgs, al final solamente hay una única partícula de Higgs. Esto es así porque los otros tres campos (reales) se convierten en los tres campos adicionales que se requieren para convertir tres partículas sin masa con dos polarizaciones físicas en partículas con masa con tres polarizaciones. Tres de los campos de Higgs se convierten en la tercera polarización de cada uno de los tres bosones gauge débiles pesados: los dos W y el Z. El cuarto campo de Higgs que queda crearía auténticas partículas de Higgs. Si este modelo es correcto, el LHC las produciría. <<

^[M21] La intensidad de cada una de las fuerzas está determinada por un coeficiente numérico. Los cálculos del grupo de renormalización muestran que los valores de estas cantidades cambian logarítmicamente con la energía. <<

^[M22] Mientras que la simetría de la fuerza débil mezcla pares de campos y la simetría de la fuerza fuerte mezcla tres campos, el grupo de simetría de la gran unificación (GUT) de Georgi-Glashow mezcla cinco campos. Algunas de las transformaciones simétricas asociadas con las fuerzas de la GUT coinciden con las transformaciones simétricas de la fuerza débil y de la fuerza fuerte. Las fuerzas se unifican porque un único grupo de simetría de transformaciones incluye todas las transformaciones simétricas del modelo estándar. <<

^[M23] Esta conexión con el espacio y el tiempo es, de hecho, más manifiesta cuando se realizan dos transformaciones supersimétricas una tras otra, primero en un orden y luego en el otro, y después se restan. En este caso, los fermiones siguen siendo fermiones y los bosones siguen siendo bosones, pero el sistema se mueve; el resultado neto de la transformación es exactamente el mismo que el de una transformación convencional del espacio-tiempo. El conmutador de las dos transformaciones supersimétricas, que realiza exactamente la misma operación que una única transformación simétrica del espacio-tiempo, demuestra decisivamente que las transformaciones supersimétricas deben estar conectadas con las simetrías que actúan sobre el espacio y el tiempo y mueven las cosas por ahí. <<

^[M24] La trayectoria de una partícula es una línea que da la posición de la partícula en función del tiempo. La trayectoria de una cuerda es una superficie que describe la posición de la cuerda entera según se mueve en el tiempo. La superficie representa el movimiento de una cuerda abierta, mientras que el tubo representa el movimiento de una cuerda cerrada. Esto se muestra en la figura A3, que ilustra el movimiento en el tiempo y las interacciones «más suaves» de las cuerdas.

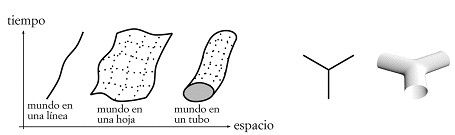
FIGURA A3. (Figura de la izquierda). El mundo en una línea de una partícula, el mundo en una hoja de una cuerda abierta y el mundo en un tubo de una cuerda cerrada. (Figura de la derecha). Interacciones de tres partículas y de tres cuerdas.

<<

^[M25] La tensión de la cuerda no es siempre tan alta como nos indica la energía de la escala de Planck. Depende de cuán intensamente interactúan las cuerdas. Joe Lykken y otros han considerado la posibilidad de que sea mucho más pequeña, caso en el que las partículas adicionales de la teoría de cuerdas podrían ser mucho más ligeras. <<

^[M26] De hecho, según la dualidad que describimos en este capítulo, incluso las sondas que se utilizan para estudiar una versión dada de la teoría de cuerdas cambian de carácter cuando el acoplamiento se hace fuerte. Así que si Ike fuera parte realmente del mundo de las cuerdas, él también cambiaría. <<

^[M27] También pueden extenderse en dimensión cero, y entonces son nuevos tipos de partículas que se llaman branas D0, o en dimensión uno, y en ese caso son nuevos tipos de cuerdas llamadas branas D1. <<

^[M28] Las branas no interactúan necesariamente a través de cargas ordinarias. Interactúan a través de una generalización en dimensión superior de las cargas. <<

^[M29] La simetría de hecho rota unas branas con otras, pero esto está fuera del alcance técnico de este libro (y haría que a Ike le diera vueltas la cabeza). <<

^[M30] Normalmente, las masas del gaugino están en una proporción de 1 : 3 : 30, donde el fotino es el más ligero, los winos vienen a continuación (aunque el zino podría ser un poco más pesado o un poco más ligero que los winos) y los gluinos son los más pesados. En los modelos secuestrados la razón es 1 : 2 : 8, donde los winos son los más ligeros, el fotino es más pesado y el gluino es, de nuevo, el más pesado. <<

^[M31] Las funciones de onda de los modos de Kaluza-Klein son los modos que aparecen en la descomposición de Fourier generalizada de la función de onda de dimensión superior. <<

^[M32] Esto también supone que no hay singularidades en la geometría del espacio-tiempo, es decir, que no hay ningún punto en el que el espacio se colapse y se haga de tamaño cero. <<

^[M33] D. Cremades, S. Franco, L. Ibáñez, F. Marchesano, R. Rabadan y A. Uranga también sugirieron una interesante alternativa. Su idea es que las partículas no están confinadas en una brana individual, sino que están, por el contrario, confinadas en las intersecciones de múltiples branas. Como en el caso de las branas separadas paralelas, las cuerdas tendidas entre branas serán generalmente pesadas. Pero las partículas ligeras o sin masa surgen de las cuerdas de longitud cero, que en este caso estarían confinadas en la región donde se cortan las branas. <<

^[M34] También podemos probar esto de un modo ligeramente diferente con un argumento más matemático. Cuando hay dimensiones enrolladas, las líneas de fuerza que parten de un objeto con masa se comportan siguiendo la ley gravitatoria de la teoría de dimensión superior a cortas distancias y siguiendo la gravedad tetradimensional a largas distancias. La única manera de reconciliar las dos leyes que rigen la fuerza y pasar suavemente de la una a la otra es observando que, aproximadamente a la distancia que corresponde a los tamaños de las dimensiones extras, las líneas de fuerza se dispersan como si hubiera solamente cuatro dimensiones, pero con una intensidad reducida a causa del volumen extra del espacio enrollado. Más allá del tamaño de las dimensiones extras, la gravedad se comporta de modo tetradimensional, pero con su intensidad reprimida por su dispersión por el volumen extradimensional.

La ley de la gravitación de Newton dice que cuando hay tres dimensiones espaciales, la fuerza es proporcional a 1/M_Pl² × 1/r². Si hay n dimensiones adicionales, la ley de la fuerza sería 1/Mⁿ⁺² × 1/ rⁿ⁺², donde M fija la intensidad de la gravedad extradimensional, igual que M_Pl fija la intensidad de la gravedad tetradimensional. Obsérvese que la ley de la fuerza de dimensión superior varía más rápidamente con r ya que las líneas de fuerza se dispersarían por una hiperesfera cuya superficie tendría n + 2 dimensiones (en vez de la superficie bidimensional de una esfera que da lugar a la ley de la fuerza en el espacio tridimensional). Sin embargo, cuando el volumen extradimensional es finito y las n dimensiones extras tienen tamaño R, la ley de la fuerza será 1/Mⁿ⁺² × 1/Rⁿ × 1/r² cuando r es más grande que R y las líneas de fuerza no pueden ya extenderse en las dimensiones extras. Ésta es la forma de una ley de fuerza en tres dimensiones espaciales si hacemos la identificación M_Pl² = Mⁿ⁺²Rⁿ. Como Rn es el volumen del espacio de dimensión superior, vemos que la intensidad de la gravedad decrece con el volumen, o equivalentemente (ya que la intensidad de la gravedad es más débil cuanto más grande es la energía de la escala de Planck), la energía de la escala de Planck es grande si el volumen es grande. <<

^[M35] Una métrica plana con tres dimensiones espaciales es ds² = dx² + dy² + dz² – c²dt². Como no hay coeficientes que dependan del espacio o del tiempo, las mediciones son independientes de dónde estamos o de en qué dirección miramos; es decir, el espacio-tiempo es completamente plano. Las tres coordenadas espaciales, así como la coordenada del tiempo (dejando a un lado el signo menos que siempre distingue el tiempo), se tratan igual; esto es, los coeficientes de los términos de la métrica son completamente independientes de la localización en el espacio y en el tiempo. <<

^[M36] La métrica en la geometría arqueada es ds² = e^k|r|(dx² + dy² + dz² – c²dt²) + dr², donde r es la coordenada de la quinta dimensión. Esto nos dice que en cualquier localización fija de la quinta dimensión, que corresponde a un r fijo, el espacio-tiempo es completamente plano. Sin embargo, el factor global que depende de r nos dice cómo medir los cambios de tamaño según la posición de un objeto en la quinta dimensión. La naturaleza exponencial negativa del coeficiente, que es el factor de arqueo, es la razón por la que la función de probabilidad del gravitón cae exponencialmente, y también la razón por la que necesitamos reajustar las escalas de la masa, la energía y el tamaño para construir una única teoría efectiva de dimensión cuatro. <<

^[M37] Como el espacio no es plano, el volumen extradimensional que entra cuando calculamos M_Pl en cuatro dimensiones no es simplemente M_Pl3R, como sería si el espacio fuera plano. Por el contrario, el valor de M_Pl depende de la curvatura. Si la métrica tiene la forma ds² = e^k|r|(dx² + dy² + dz² – c²dt²) + dr², donde r es la coordenada de la quinta dimensión, entonces, más o menos, M_Pl² = M3/k. En otras palabras, el tamaño del espacio es, en gran medida, irrelevante. Esto tiene sentido porque la curvatura del espacio —no el tamaño de la dimensión extra— determina cómo las líneas del campo se extienden en la dimensión extra y de aquí la intensidad de la gravedad tetradimensional. De hecho, hay una pequeña dependencia respecto de R: la fórmula real es M_Pl² = M³/k(1 – e^–kR), pero cuando kR es grande, el término exponencial es, en gran medida, irrelevante y puede ser despreciado. <<

^[M38] El factor de arqueo en el modelo de la gravedad localizada localmente que Andreas Karch y yo desarrollamos es la suma de una función exponencial decreciente (como en las geometrías arqueadas que hemos considerado ya) y una función exponencial creciente. Es proporcional a cosh(kc – k|r|), donde k está relacionada con la energía del bulto y c está relacionada con la energía de la brana. Como el factor de arqueo de la gravedad localizada que hemos considerado ya, este factor de arqueo cae exponencialmente según uno se aleja de la brana. Pero, al contrario que en el caso anterior, el factor de arqueo se da la vuelta y entonces crece exponencialmente. El gravitón tetradimensional está localizado en la región comprendida entre la brana y este «punto de inversión». Más allá de esta distancia, la gravedad tetradimensional ya no tiene ninguna vigencia. <<

^[M39] La T-dualidad intercambia el radio de compactación r y su inverso 1/r (con las distancias medidas en unidades de longitud de la cuerda). <<

^[M40] Los físicos Csaba Csaki, Joshua Erlich y Christophe Grojean han hecho, sin embargo, la interesante observación de que la velocidad de la luz y la velocidad de la gravedad pueden ser diferentes (la velocidad de la gravedad puede, de hecho, ser superior) si hay un espacio-tiempo arqueado asimétricamente en el que los ajustes de escala de las coordenadas del tiempo y las espaciales a lo largo de la quinta dimensión son diferentes entre sí. <<