22

PASILLO PROFUNDO:

UNA DIMENSIÓN EXTRA INFINITA

El espacio-tiempo curvado tiene propiedades notables. Exploramos algunas de ellas en el capítulo 20; tal es el caso de la manera en la que la masa, el tamaño y la intensidad de la gravedad pueden depender de la posición. Este capítulo presenta una propiedad todavía más extraordinaria del espacio-tiempo curvado: puede parecer que cuenta con cuatro dimensiones, aunque, verdaderamente, tenga cinco. Examinando más cuidadosamente la geometría arqueada del espacio-tiempo, Raman y yo nos percatamos, con asombro, de que incluso una dimensión extra infinita puede a veces ser invisible.

La geometría del espacio-tiempo que consideraremos en este capítulo es casi la misma que la descrita en el capítulo 20. Pero, como sugiere la historia de arriba, esta geometría presenta un único rasgo distintivo: tiene sólo una brana. Pero ésta es una distinción de una importancia tremenda: como no hay una segunda brana confinante, una única brana implica que la quinta dimensión es infinita (véase la figura 86).

FIGURA 86. El espacio-tiempo infinito con una única brana. Hay una única brana tetradimensional en un universo de dimensión cinco. El modelo estándar reside en esta única brana.

Ésta es una diferencia formidable. Durante tres cuartas partes de un siglo, desde que Theodor Kaluza introdujo la idea de una dimensión extra del espacio en 1919, los físicos creyeron que las dimensiones extras eran aceptables, pero sólo si eran de tamaño finito, o bien si estaban enrolladas o confinadas entre branas. Se suponía que las dimensiones extras infinitas eran muy fáciles de descartar porque la fuerza gravitatoria, que se extendería hasta el infinito en estas dimensiones, sería incorrecta en todas las escalas de distancia, incluso en aquéllas que ya conocemos. Se suponía que una quinta dimensión infinita desestabilizaría todo lo que nos rodea, incluso el sistema solar, que se mantiene unido por la física newtoniana.

Este capítulo explica por qué este razonamiento no siempre es correcto. Investigaremos una razón enteramente nueva por la que las dimensiones extras podrían estar ocultas, una razón que Raman y yo descubrimos en 1999. El espacio-tiempo puede estar arqueado de modo que el campo gravitatorio se concentre intensamente en una pequeña región cerca de una brana, y que esté tan concentrado en ella que la enorme expansión de una dimensión infinita no trae consecuencias. La fuerza gravitatoria no se pierde en las dimensiones extras, sino que permanece concentrada en una pequeña región cerca de una brana.

En este contexto, el gravitón, la partícula que transmite la gravedad, está localizado cerca de una brana, que es la brana de la historia de Atenea, pero que, a partir de ahora, voy a llamar la Brana de la Gravedad. El sueño de Atenea la llevó hasta este espacio arqueado de dimensión cinco, en el que la Brana de la Gravedad altera tan radicalmente la naturaleza del espacio-tiempo que el espacio parece ser tetradimensional, aunque, en realidad, es de dimensión cinco. Notablemente, una dimensión superior arqueada puede tener una extensión infinita y, sin embargo, estar oculta, mientras que las tres dimensiones infinitas planas reproducen la física de nuestro mundo.

El gravitón localizado

El lector quizá recuerde que la primera vez que introduje las branas distinguí entre la resistencia a explorar regiones lejanas y el confinamiento genuino, que prohíbe explícitamente viajar más allá del lugar donde alguien o algo está confinado. Aunque probablemente no hayamos visitado nunca Groenlandia, no hay ninguna ley que nos prohíba ir allí. Pero hay algunos sitios adonde, sencillamente, es problemático llegar. Aunque esté permitido viajar a esos lugares e incluso éstos no estén más lejos que otros a los que sí hemos ido, es muy probable que jamás los visitemos.

O imaginémonos a alguien a quien se le ha roto una pierna. En principio, podría salir de casa cuando quisiera, pero es mucho más probable que se encuentre dentro de la vivienda que fuera, aunque no haya barrotes ni candados que le retengan allí.

Análogamente, el gravitón localizado tiene acceso sin restricciones a una quinta dimensión infinita. Pero, sin embargo, está fuertemente concentrado en las cercanías de una brana y tiene una probabilidad muy pequeña de encontrarse lejos de ella. Según la relatividad general, todo —incluido el gravitón— está sujeto a la fuerza gravitatoria. El gravitón no es en absoluto especial, pero se comporta como si fuera atraído gravitatoriamente hacia la brana y, por lo tanto, permanece cerca de ella. Y como el gravitón sólo viaja muy raramente fuera de una región limitada, la dimensión extra puede ser infinita sin producir ningún efecto peligroso que obligue a descartar la teoría.

En nuestro trabajo, Raman y yo nos concentramos en la gravedad en un espacio-tiempo de dimensión cinco con una única dimensión extra del espacio. Pudimos así concentrarnos en el mecanismo de localización que ahora vamos a discutir, que mantiene la gravedad recluida en una pequeña región del espacio-tiempo de dimensión cinco. Supondré que, si el universo tiene diez o más dimensiones, una combinación entre la localización y el enrollamiento mantiene ocultas el resto. Dichas dimensiones ocultas adicionales no afectarían al fenómeno de localización que voy a describir enseguida, de modo que haré caso omiso de ellas y me concentraré en las cinco dimensiones que son cruciales para nuestra discusión.

En nuestro modelo hay una única brana en uno de los extremos de la quinta dimensión del espacio-tiempo. Es reflexiva, como lo eran las dos branas que describí en el capítulo 20. Las cosas que chocan contra la brana, sencillamente, rebotan, de modo que nada pierde energía cuando golpea la brana. Como el modelo que estamos considerando ahora contiene sólo esta única brana, supondremos que las partículas del modelo estándar están confinadas allí; nótese la diferencia con el modelo que discutí en el capítulo anterior, en el que las partículas del modelo estándar estaban en la Brana Débil, que aquí ya no existe. La localización de las partículas del modelo estándar no es relevante para la geometría del espacio-tiempo, pero tiene, por supuesto, implicaciones para la física de partículas.

Aunque en este capítulo estamos interesados en la teoría con una única brana, la primera pista que Raman y yo tuvimos de que podía legitimarse una quinta dimensión infinita fue un rasgo curioso de la geometría arqueada con dos branas. Inicialmente supusimos que la segunda brana servía para dos cosas. En primer lugar, para confinar las partículas del modelo estándar; en segundo lugar, para hacer que la quinta dimensión sea finita. Como en el caso de las dimensiones extras planas, una quinta dimensión finita garantizaba que, a distancias suficientemente largas, la gravedad sería la de un espacio-tiempo tetradimensional.

Sin embargo, un hecho peculiar sugirió que este último papel de la segunda brana era un señuelo para despistar y que la segunda brana no era esencial para que la gravedad pudiera imitar la de un universo auténticamente tetradimensional: las interacciones del gravitón tetradimensional eran virtualmente independientes del tamaño de la quinta dimensión. Un cálculo mostraba que la gravedad tendría la misma intensidad si la segunda brana permanecía donde estaba o si estaba dos veces más lejos que la Brana de la Gravedad, o si estaba diez veces más lejos, adentrada en el bulto, muy lejos de la primera brana. De hecho, la gravedad tetradimensional persistía incluso si nuestro modelo ponía la segunda brana en el infinito, es decir, si sencillamente la eliminaba. Esto no sería cierto si la segunda brana y una dimensión finita fueran esenciales para reproducir la gravedad tetradimensional.

Ésta fue nuestra primera pista de que la intuición de que necesitamos una segunda brana se basaba en las dimensiones planas y que no era necesariamente cierta en el espacio-tiempo arqueado. Con una dimensión extra plana, la segunda brana es obligatoria para la gravedad tetradimensional. Podemos ver esto con ayuda del ejemplo del aspersor del capítulo 20. Una dimensión extra plana correspondería al hecho de que el agua se distribuye equitativamente por todas partes a lo largo de un aspersor recto largo (véase la figura 81, p. 553).^[132] Cuanto más largo fuera el aspersor, menos agua caería en un jardín dado. Si hubiera que extender este razonamiento a un aspersor infinitamente largo, veríamos que el agua se reparte de manera tan dispersa que, esencialmente, no caería nada de agua en un jardín dado de área finita.

Análogamente, si la gravedad se extendiera a lo largo y ancho de una dimensión uniforme infinita, la fuerza gravitatoria estaría tan atenuada a lo largo de la dimensión extra que quedaría reducida a nada. Una geometría con una dimensión extra infinita tendría que contener alguna sutileza que fuera más allá de esta descripción intuitiva simple, si la gravedad ha de comportarse como si fuera tetradimensional. Y, en efecto, el espacio-tiempo arqueado proporciona el ingrediente añadido que se requiere.

Para ver cómo funciona esto, usemos otra vez el ejemplo del aspersor para identificar la brecha que presenta el argumento de arriba. Supongamos que tenemos un aspersor infinitamente largo, pero que no distribuimos el agua equitativamente por todas partes. Por el contrario, tenemos el control de cómo se reparte el agua, con la opción de asegurar que nuestro propio jardín esté bien regado. Una manera de conseguir esto sería destinar la mitad del agua a nuestra porción de tierra y la mitad restante del agua al resto de las tierras. En este caso, aunque los jardines lejanos recibirían un trato injusto, estaría garantizado que nuestro jardín recibiría el agua que necesita. Nuestro jardín siempre recibiría la mitad del agua, aunque el aspersor continuara enviando agua indefinidamente lejos. Con una distribución desigual del agua, conseguiríamos toda el agua que necesitamos. El aspersor podría ser infinito, pero a nosotros nos daría igual su longitud.

Análogamente, la función de probabilidad del gravitón en nuestra geometría arqueada es siempre muy grande cerca de la Brana de la Gravedad, a pesar de la quinta dimensión infinita. Como en el capítulo anterior, la función de probabilidad del gravitón se dispara en esta brana (véase la figura 87) y cae exponencialmente, según el gravitón se aleja de la Brana de la Gravedad por la quinta dimensión. En esta teoría, sin embargo, la función de probabilidad del gravitón continúa indefinidamente lejos, pero esto no trae consecuencias para el tamaño de la función de probabilidad del gravitón cerca de la brana.

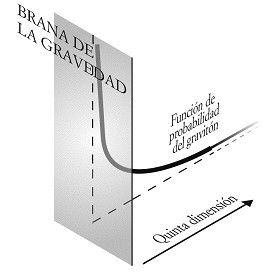
FIGURA 87. La función de probabilidad del gravitón en un espacio-tiempo infinito arqueado con una sola brana.

Este tipo de función de probabilidad que cae en picado nos dice que la probabilidad de encontrar un gravitón lejos de la Brana de la Gravedad es minúscula, tan minúscula que generalmente podemos olvidarnos de las regiones lejanas de la quinta dimensión. Aunque, en principio, el gravitón puede estar dondequiera en la quinta dimensión, el decrecimiento exponencial hace que la función de probabilidad del gravitón esté muy concentrada en las cercanías de la Brana de la Gravedad. La situación es casi la misma, pero no exactamente, que la producida por una segunda brana que confinara el gravitón en una región acotada.

La alta probabilidad de que el gravitón se encuentre cerca de la Brana de la Gravedad, y la correspondiente concentración del campo gravitatorio allí, podría compararse también a la alta probabilidad de que los patos glotones se concentren en un estanque cerca de la orilla. Normalmente los patos no están distribuidos equitativamente a lo largo y ancho del estanque, sino que más bien se concentran en torno a los pedazos de pan que los aficionados a las aves arrojan al agua (véase la figura 88). De modo que el tamaño del estanque sería esencialmente irrelevante en lo que afecta a la distribución de los patos. Análogamente, en el espacio-tiempo arqueado, la gravitación atrae al gravitón hacia la Brana de la Gravedad, de modo que la extensión de la quinta dimensión es irrelevante.

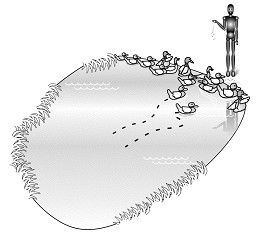
FIGURA 88. Si los patos se concentran cerca de la orilla, podemos contarlos casi todos con sólo contar los que están más cerca.

También podemos ver por qué la quinta dimensión no afecta demasiado a la gravedad considerando el campo gravitatorio que rodea un objeto en la Brana de la Gravedad. Hemos visto que, en las dimensiones espaciales planas, las líneas de fuerza que emanan de un objeto se dispersan equitativamente en todas las direcciones. Y cuando hay dimensiones extras finitas, las líneas de campo se extienden en todas las direcciones hasta que algunas alcanzan el borde y se desvían. Por esta razón, las líneas del campo gravitatorio de un objeto que están a una distancia más grande que el tamaño de las dimensiones extras se dispersan solamente a lo largo de las tres dimensiones infinitas del mundo de dimensión inferior.

FIGURA 89. En la teoría arqueada, las líneas de campo están distribuidas equitativamente por todas las direcciones de la brana. Sin embargo, al salir de la brana, las líneas de campo vuelven atrás, de modo que siguen un camino esencialmente paralelo a la brana, casi como si la quinta dimensión fuera finita. Incluso con una dimensión infinita, el campo gravitatorio está localizado cerca de la brana y las líneas de campo se dispersan esencialmente, como si hubiera sólo cuatro dimensiones (del espacio-tiempo).

En el contexto de la geometría arqueada, por el contrario, las líneas de campo no se distribuyen equitativamente en todas las direcciones. Perpendicularmente a la brana se extienden muy poco (véase la figura 89). Como las líneas del campo gravitatorio se dispersan principalmente a lo largo de la brana, el campo gravitatorio parece casi idéntico al campo asociado a un objeto en cuatro dimensiones. La dispersión en la quinta dimensión es tan pequeña (no mucho más grande que la longitud de la escala de Planck, 10^–33 cm) que podemos hacer caso omiso de ella. Aunque la dimensión extra es infinita, resulta irrelevante para el campo gravitatorio de un objeto confinado en una brana.

Podemos ver también cómo Raman y yo resolvimos el enigma inicial al que nos enfrentamos: ¿por qué el tamaño de la quinta dimensión es irrelevante para la intensidad de la gravedad? Volviendo al ejemplo del aspersor, supongamos que especificamos ahora la distribución de agua sobre el aspersor entero, de modo que refleje la distribución de la gravedad de la función de probabilidad que cae en picado del gravitón: después de tomar la mitad del agua para nuestro jardín, enviamos la mitad del agua que queda al jardín colindante, la mitad de esta última cantidad al jardín siguiente y así sucesivamente, de manera que cada jardín va recibiendo la mitad del agua que recibió el anterior. Para reflejar la situación de una segunda brana en la quinta dimensión, supondremos que dejamos de suministrar agua en un cierto punto, al igual que una segunda brana en la quinta dimensión cortaría la función de probabilidad del gravitón en algún punto de la quinta dimensión. Y para reflejar una quinta dimensión infinita, supondremos que el aspersor distribuye agua indefinidamente a lo largo de todo su recorrido.

Para demostrar que el tamaño de la quinta dimensión es irrelevante para la intensidad de la gravedad cerca de la brana, quisiéramos probar que los primeros jardines consiguen casi la misma cantidad de agua, independientemente de que dejemos de transportar agua al llegar al quinto jardín o al décimo jardín o de que sigamos distribuyendo agua indefinidamente. Consideremos entonces qué es lo que pasa si el aspersor se apaga después del quinto jardín. Como al sexto jardín y a los siguientes les iba a tocar tan poca agua, la cantidad total de agua que el aspersor destinaría a los primeros jardines diferiría de la cantidad total de un aspersor infinito solamente en un pequeño porcentaje. Y si apagásemos el aspersor después del séptimo jardín, ese porcentaje sería todavía más pequeño. Con nuestra distribución del agua, en la que casi toda el agua está destinada a los primeros jardines, los jardines lejanos, que reciben solamente una proporción diminuta del agua, son irrelevantes en relación con las cantidades de agua que reciben los primeros jardines.^[133]

Como usaré de nuevo el ejemplo de los patos en el próximo capítulo, explicaré ahora lo mismo en términos de contar patos atraídos hacia la orilla, donde alguien ha echado pan. Si nos pusiéramos a contar primero los patos cercanos y luego los que están un poco más lejos, pronto nuestra actividad de recuento de patos se volvería casi inútil. Cuando llegase el momento de separar un poco nuestra vista de la orilla, quedarían ya muy pocos patos que contar. No es preciso seguir contando patos que estén lejos de la orilla porque, esencialmente, ya los hemos contado todos al concentrarnos en la región que estaba cerca de la orilla (véase la figura 88).

La función de probabilidad del gravitón es sencillamente tan pequeña más allá de la segunda brana que la colocación de una segunda brana produciría sólo una diferencia insignificante en la intensidad de interacción del gravitón tetradimensional. En otras palabras, la extensión de la quinta dimensión es irrelevante para la intensidad aparente de la gravedad tetradimensional en esta teoría, en la que el campo gravitatorio está localizado cerca de la Brana de la Gravedad.^[M37] Aunque no haya una segunda brana y la quinta dimensión sea infinita, la gravedad sigue pareciendo tetradimensional.

Raman y yo llamamos a esta situación gravedad localizada. La razón es que la función de probabilidad del gravitón está localizada cerca de una brana. Aunque, hablando estrictamente, la gravedad puede trascender a la quinta dimensión porque la quinta dimensión es en efecto infinita, en realidad no lo hace a causa de la poca probabilidad que hay de que el gravitón se encuentre lejos. El espacio no está truncado y sin embargo todo permanece en una región concentrada en las cercanías de la brana. Una brana alejada no produce ninguna diferencia en los procesos físicos de la Brana de la Gravedad, ya que muy pocas cosas de la Brana de la Gravedad se aventuran a irse lejos. Todo lo que se produce en la Brana de la Gravedad o cerca de ella permanece próximo a ella, en una región localizada.

Algunas veces los físicos se refieren a este modelo de la gravedad localizada como RS2. RS alude a Randall y Sundrum, pero el 2 es confuso: se refiere al hecho de que éste es el segundo artículo que escribimos sobre geometría arqueada, y no al hecho de que haya dos branas. La teoría con dos branas, que aborda el problema de la jerarquía, se conoce como RS1. (Los nombres serían menos confusos si hubiésemos escrito los artículos en orden inverso). Al contrario que en el caso de RS1, la teoría de este capítulo no es necesariamente relevante para el problema de la jerarquía, aunque uno puede introducir una segunda brana y resolver también el problema de la jerarquía, como consideramos brevemente hacia el final del capítulo 20. Pero haya o no haya una segunda brana en el espacio para abordar el problema de la jerarquía, la gravedad localizada es una posibilidad radical con importantes implicaciones teóricas, la cual contradice la hipótesis largo tiempo defendida de que las dimensiones extras tienen que ser compactas.

Compañeras Kaluza-Klein del gravitón

En la sección previa se discutió la función de probabilidad del gravitón, que está fuertemente concentrada en la Brana de la Gravedad. La partícula sobre la que se hablaba desempeña el papel del gravitón tetradimensional porque viaja casi exclusivamente a lo largo de la brana y tiene sólo una probabilidad minúscula de trascender a la quinta dimensión. Desde el punto de vista del gravitón, parece como si el espacio tuviera una quinta dimensión de sólo 10^–33 cm (un tamaño fijado por la curvatura, que, a su vez, está determinada por la energía que tiene el bulto y la brana) más que de tamaño infinito.

Pero, aunque Raman y yo estábamos bastante entusiasmados con nuestro descubrimiento, no teníamos la seguridad de haber resuelto completamente el problema. ¿Era el gravitón localizado suficiente para generar por sí mismo una teoría efectiva tetradimensional en la que la gravedad se comportara como lo haría en cuatro dimensiones? El problema en potencia era que las compañeras de Kaluza-Klein del gravitón podrían también contribuir a la fuerza gravitatoria y modificar así significativamente la gravedad.

La razón por la que esto parecía tan peligroso consistía en que, generalmente, cuanto más grande es el tamaño de la dimensión extra, más pequeña es la masa de la partícula KK más ligera. Para nuestra teoría con una dimensión infinita, esto significaría que la partícula KK más ligera podría ser arbitrariamente ligera. Y como la diferencia en masas de las partículas KK también decrece con el tamaño de la dimensión extra, podrían producirse en cualquier energía finita infinidad de tipos de compañeras KK del gravitón muy ligeras. Todas estas partículas KK podrían contribuir potencialmente a la ley de la fuerza gravitatoria y cambiarla. El problema parecía especialmente endiablado porque aunque cada partícula KK interactuase muy débilmente, si hubiera muchas de ellas, entonces la fuerza gravitatoria tendría, no obstante, un aspecto bastante diferente del que tiene en cuatro dimensiones.

Y encima, como las partículas KK son muy ligeras, serían muy fáciles de producir. Los aceleradores están ya operando a energías suficientemente altas como para producirlas. Hasta algunos procesos físicos ordinarios, como ciertas reacciones químicas, generarían la energía suficiente para crear compañeras KK del gravitón. Si las partículas KK aportasen demasiada energía al bulto de dimensión cinco, habría que desechar la teoría.

Afortunadamente, ninguno de estos asuntos resulta ser un problema. Cuando calculamos las funciones de probabilidad de las partículas KK, descubrimos que las compañeras KK del gravitón interactúan de un modo extremadamente débil en la Brana de la Gravedad o cerca de ella. A pesar del gran número de compañeras KK del gravitón, todas interactúan tan débilmente que no hay peligro de producir demasiadas de ellas ni de cambiar la forma de la ley de la fuerza gravitatoria en ninguna parte. Si hay algún problema, consiste en que esta teoría imita tan bien la gravedad tetradimensional que ¡todavía no conocemos ningún medio de distinguirla experimentalmente de un mundo verdaderamente tetradimensional! Las compañeras KK del gravitón tendrían un impacto tan insignificante en cualquier cosa observable que todavía no sabemos cómo distinguir la diferencia entre cuatro dimensiones planas y cuatro dimensiones planas complementadas por una quinta arqueada.

Podemos entender la debilidad de las interacciones de las compañeras KK del gravitón a partir de la forma de sus funciones de probabilidad. Como en el caso del gravitón, éstas nos dicen la probabilidad de que una partícula se encuentre en un punto dado de la quinta dimensión. Raman y yo seguimos el procedimiento más o menos estándar para encontrar las masas y las funciones de probabilidad de cada compañera KK del gravitón en nuestra geometría arqueada. Esto implicaba la resolución de un problema de mecánica cuántica.

Para una quinta dimensión plana, el problema de la mecánica cuántica, descrito en el capítulo 6, consistía en encontrar las ondas que encajan en la dimensión enrollada y cuantizar así las energías permitidas.^[134] Para nuestra geometría arqueada infinita de dimensión cinco, el problema cuántico parecía bastante diferente, ya que necesitábamos tener en cuenta la energía que había en la brana y en el bulto y que alabeaba el espacio-tiempo. Pero conseguimos modificar el procedimiento estándar para que se adaptara a nuestro contexto. Los resultados fueron fascinantes.

La primera partícula KK que encontramos fue la que no tiene momento en la quinta dimensión. La función de probabilidad de esta partícula está fuertemente concentrada en la Brana de la Gravedad y decrece exponencialmente al alejarnos de ella. Esta forma debería resultarnos familiar: es la función de probabilidad para el mismo gravitón tetradimensional que hemos discutido ya. Este modo KK sin masa es el gravitón tetradimensional que transmite la ley de la fuerza de Newton tetradimensional.

El resto de las partículas KK son, sin embargo, muy diferentes. Es muy poco probable que alguna de estas otras partículas se encuentre cerca de la Brana de la Gravedad. Por el contrario, lo que se descubre es que, para cualquier valor de la masa entre cero y la masa de la escala de Planck, existe una partícula KK con esa masa concreta y la función de probabilidad para cada una de esas partículas se dispara en un punto diferente a lo largo de la quinta dimensión.

De hecho, hay una interpretación interesante de la localización de los diferentes picos. Vimos en el capítulo 20 que en el espacio-tiempo arqueado, para poner a todas las partículas al mismo nivel en la teoría efectiva tetradimensional de modo que todas interactúen con la gravedad del mismo modo, reajustamos las escalas de las distancias, tiempos, energías y momentos diferentemente a lo largo de la quinta dimensión. Según uno se aleja de la brana, cada punto queda asociado a una energía exponencialmente más baja. Por eso se esperaba que las partículas de la Brana Débil tuvieran una masa de aproximadamente un TeV. La sombra de Atenea cuando viajaba en la quinta dimensión se hacía más grande y Atenea misma se hacía más ligera al alejarse de la Brana de la Gravedad y al aproximarse a la Brana Débil.

Cada punto a lo largo de la quinta dimensión puede asociarse a una masa determinada del mismo modo; la masa está relacionada con la masa de la escala de Planck por el reajuste de escala en ese punto. Y la partícula KK cuya función de gravedad se dispara en ese punto concreto tiene aproximadamente esa masa de Planck reajustada. Al ir adentrándose uno en la quinta dimensión, va encontrando partículas KK cada vez más ligeras, cuyas funciones de probabilidad se disparan allí.

De hecho, podríamos decir que el espectro de Kaluza-Klein exhibe una sociedad muy segregada. Las partículas KK pesadas están desterradas de las regiones del espacio en las que la energía reajustada es demasiado pequeña para producirlas. Y las partículas KK ligeras se encuentran raramente en aquellas regiones que contienen partículas con mucha energía. Las partículas KK se concentran lo más lejos que pueden de la Brana Débil, dada su masa. Sus localizaciones son como la talla de los pantalones de los adolescentes, esto es, lo más holgados posible sin llegar a caerse. Por suerte, las leyes físicas que determinan las localizaciones de las partículas KK resultan más fáciles de comprender que las reglas de la moda adolescente, que son mucho más enrevesadas.

Para nosotros, la propiedad más importante de las funciones de probabilidad de las partículas KK ligeras es que éstas son extremadamente pequeñas en la Brana de la Gravedad. Esto significa que sólo hay una pequeña probabilidad de encontrar partículas KK ligeras en ella o cerca de ella. Como las partículas KK ligeras huyen lo más lejos que pueden de la Brana de la Gravedad, las partículas ligeras (aparte del gravitón, que es excepcional y cuya función de probabilidad se dispara en la Brana de la Gravedad) se producirían muy raramente allí. Además, las partículas KK ligeras no modifican significativamente la ley de la fuerza gravitatoria porque tienden a mantenerse lejos de la Brana de la Gravedad y, por lo tanto, no interactúan mucho con las partículas confinadas en la brana.

Juntándolo todo, Raman y yo llegamos a la conclusión de que habíamos descubierto una teoría que funcionaba. El gravitón localizado en la Brana de la Gravedad es el responsable de la aparición de la gravedad tetradimensional. A pesar de la abundancia de compañeras KK del gravitón, éstas interactúan tan débilmente en la Brana de la Gravedad que su efecto es insignificante. Y, a pesar de la existencia de una quinta dimensión infinita, todas las leyes y los procesos físicos, incluida la ley de la gravedad, parecen concordar con lo que se espera de un mundo tetradimensional. En este espacio fuertemente arqueado es permisible una dimensión extra infinita.

Como se mencionó antes, cabe afirmar que este modelo es frustrante desde el punto de vista de la física de las observaciones. Por sorprendente que parezca, este modelo de dimensión cinco imita las cuatro dimensiones tan extraordinariamente bien que será sumamente complicado dilucidar si tiene o no vigencia. Los experimentadores de la física de partículas van a vivir, ciertamente, tiempos difíciles.

Los físicos han comenzado, sin embargo, a explorar propiedades astrofísicas y cosmológicas que podrían distinguir los dos mundos. Muchos físicos^[135] han examinado los agujeros negros en el espacio-tiempo arqueado y continúan investigando si existen propiedades características que podamos usar para determinar en qué tipo de universo vivimos realmente.

Por ahora, sabemos que la localización es una posibilidad teórica nueva y fascinante para las dimensiones extras en nuestro universo. Yo espero con impaciencia los nuevos avances que podrían finalmente determinar si ésta es o no una propiedad verdadera de nuestro mundo.