11

LAS ESCALAS Y LA GRAN UNIFICACIÓN:

LA RELACIÓN ENTRE INTERACCIONES A DIFERENTES DISTANCIAS Y ENERGÍAS

Vamos a ver que la frase que, en un principio, oyó Atenea es cierta. Este capítulo trata de cómo los procesos físicos que se producen entre partículas separadas una cierta distancia pueden estar relacionados con los que se producen a otras distancias y de por qué las magnitudes físicas, como la masa de una partícula o la fuerza de interacción, dependen de la energía de la partícula. Esta dependencia respecto de la energía y la distancia es, además, la clásica dependencia de las fuerzas con respecto a la distancia. Por ejemplo, clásicamente, la fuerza del electromagnetismo, como la de la gravedad, decrece en proporción al cuadrado de la distancia entre los objetos que interactúan (la ley del cuadrado del inverso). Pero la mecánica cuántica modifica esta dependencia respecto a la distancia influyendo sobre la propia fuerza de interacción, de modo que las partículas que están a distintas distancias (y con distintas energías) parecen interactuar con cargas distintas.

Las fuerzas se hacen más débiles o más fuertes dependiendo de las distancias como resultado de las partículas virtuales: partículas de vida breve que existen como consecuencia de la mecánica cuántica y del principio de incertidumbre. Las partículas virtuales interactúan con los bosones gauge y alteran las fuerzas, de modo que su efecto depende de las distancias, algo muy parecido al proceso mediante el cual los amigos de Atenea distorsionaron el mensaje al transmitírselo de unos a otros.

La teoría cuántica de campos nos dice cómo se calcula el efecto de las partículas virtuales sobre la dependencia de las fuerzas con respecto a la distancia y la energía. Un triunfo de estos cálculos fue la explicación de por qué la fuerza fuerte es así de fuerte. Otra consecuencia importante fue la existencia potencial de una gran teoría unificada, en la que las tres fuerzas no gravitatorias, que son tan diferentes a bajas energías, se funden en una sola fuerza unificada a altas energías. Exploraremos estos dos resultados, así como las ideas y los cálculos de la teoría cuántica de campos en los que se basan.

Al leer los próximos capítulos, habrá que tener en mente lo muy dispares que son las escalas de energía que estamos discutiendo. La energía de unificación es aproximadamente mil billones de GeV, y la energía de la escala de Planck, en la que la gravedad se hace fuerte, es aproximadamente mil veces más grande. La energía de la escala débil, que es la energía a la que normalmente se realizan los experimentos, es tremendamente más pequeña: aproximadamente entre cien y mil GeV. La energía de la escala débil, comparada con la energía de unificación, es tan pequeña como el tamaño de una canica comparado con la distancia entre la Tierra y el Sol. Consecuentemente, a veces diré que la energía de la escala débil es baja aunque es una energía alta desde el punto de vista de los experimentos,^[84] ya que es muchísimo más pequeña que la energía de unificación y también que la energía de la escala de Planck.

El enfoque de cerca y el de lejos

Las teorías de campos efectivas aplican la idea de las teorías efectivas sobre las que hablamos en el capítulo primero a la teoría cuántica de campos. Se concentran sólo en aquellas escalas de energía y de distancia que esperamos poder medir. La teoría de campos efectiva que se aplica a una escala de energía o de distancia determinada describe «efectivamente» aquellas energías o distancias que necesitamos tener en cuenta. Se concentra en aquellas fuerzas e interacciones que pueden darse cuando las partículas tienen esa energía determinada (o más baja)^[85] e ignora todas las energías que son inaccesiblemente más altas. No reclama los detalles de los procesos físicos o de las partículas que surgen sólo a energías más altas de las que podemos alcanzar.

Una de las ventajas de una teoría de campos efectiva es que, aunque no conozcamos qué interacciones tienen lugar a distancias cortas, podemos de todos modos estudiar las cantidades que cuentan en las escalas que nos interesan. En realidad solamente necesitamos pensar en las magnitudes que, en principio, podemos detectar. Cuando mezclamos pintura, no necesitamos saber su estructura molecular detallada. Pero probablemente queramos saber las propiedades que percibimos fácilmente, como el color y la textura. Con esta información, aunque no sepamos la microestructura de la pintura, podríamos clasificar las propiedades relevantes de las pinturas y predecir qué efecto presentarán las mezclas de las pinturas cuando las apliquemos al lienzo.

Sin embargo, si supiéramos la composición química de la pintura, las reglas de la física nos permitirían también deducir algunas de esas propiedades. Cuando estamos pintando (usando la teoría efectiva) no necesitamos esta información, pero sí que la encontraríamos útil si estuviéramos fabricando pintura (deduciendo los parámetros de la teoría efectiva a partir de una teoría más fundamental).

Análogamente, si no conocemos la teoría a corta distancia (alta energía), no seremos capaces de deducir magnitudes mensurables. Sin embargo, cuando conocemos los detalles a distancias cortas, la teoría cuántica de campos nos dice precisamente cómo relacionar entre sí las diferentes teorías efectivas que se aplican a las diferentes energías. Nos permite deducir las magnitudes de una de las teorías efectivas a partir de las magnitudes de otra.

El método para calcular cómo dependen las magnitudes de la energía y de la distancia, que fue desarrollado por vez primera por Kenneth Wilson en 1974, tiene un nombre caprichoso: el grupo de renormalización. Además de las simetrías, dos de las herramientas más poderosas de la física son el concepto de teoría efectiva y el grupo de renormalización, y ambos involucran procesos físicos con escalas de distancia o energía muy diferentes. La palabra grupo es un término matemático que se consolidó, aunque su origen matemático es bastante irrelevante.

Sin embargo, la palabra renormalización no es del todo mala. Se refiere al hecho de que a cada escala de distancias de interés, nos paramos un momento para orientarnos. Determinamos qué partículas y qué interacciones son relevantes para las energías concretas que nos interesan en ese momento. Y entonces aplicamos una nueva normalización —esto es, una nueva calibración— para todos los parámetros de la teoría.

El grupo de renormalización emplea ideas que son semejantes a las presentadas en el capítulo 2, en el que discutimos la viabilidad de interpretar una teoría de dimensión superior en un lenguaje de dimensión inferior y tratamos una teoría bidimensional que tenía una pequeña dimensión enrollada como si fuera solamente unidimensional. Cuando enrollábamos dimensiones, ignorábamos todos los detalles de lo que ocurría dentro de las dimensiones extras y suponíamos que podía describirse todo en términos de dimensión inferior. Nuestra nueva «normalización» era la descripción en dimensión cuatro, que podía usarse cuando nos concentrábamos en grandes distancias.

Podemos seguir un proceso muy parecido para deducir una teoría que se aplique a distancias largas a partir de cualquier teoría que sea apropiada para distancias cortas: decidir cuál es la distancia mínima que nos interesa y «limpiar» la física relevante a distancias más cortas. Un modo de hacer esto es determinar el valor medio de aquellas cantidades cuyos detalles determinarían una diferencia solamente en las distancias cortas que hemos decidido ignorar. Si tenemos un retículo lleno de puntos en una escala de grises, literalmente haríamos la media de la densidad de gris de los puntos más pequeños para calcular la intensidad de gris que habría que dar a puntos más grandes, de modo que reprodujeran el mismo efecto que antes. Los ojos hacen esto automáticamente cuando vemos algo con una resolución borrosa.

Si podemos ver las cosas sólo con un nivel dado de precisión, no necesitamos saber qué pasa a escalas más reducidas para hacer cálculos útiles que relacionen las magnitudes mensurables. Nuestra línea de conducta más efectiva suele implicar la elección del «tamaño del punto» en la teoría, de modo que éste concuerde con nuestro nivel de precisión. De esta manera podemos desdeñar las partículas pesadas que nunca se producirán y las interacciones a corta distancia que nunca se darán. En su lugar, podemos concentrar los cálculos en las partículas e interacciones que son relevantes en la energía que podemos conseguir.

No obstante, si conocemos la teoría más precisa que rige a distancias más cortas, podemos usar esta información para calcular magnitudes en la teoría efectiva que nos interesa, o sea, la teoría efectiva con una resolución más baja. Al igual que ocurre con la escala de grises, cuando pasamos de una teoría efectiva con una determinada resolución a corta distancia, a otra con una resolución menos precisa, en esencia lo que hacemos es cambiar el «tamaño del punto» con el que decidimos analizar la teoría. El grupo de renormalización nos dice cómo calcular la influencia que podrían tener esas interacciones a corta distancia sobre las partículas en la teoría a largas distancias. Extrapolamos así los procesos físicos de una escala de distancia o de energía a otra.

Partículas virtuales

Los cálculos del grupo de renormalización hacen estas extrapolaciones teniendo en cuenta el efecto de los procesos de la mecánica cuántica y las partículas virtuales. Las partículas virtuales, consecuencia de la mecánica cuántica, son gemelas extrañas y fantasmales de las partículas reales. Irrumpen en el mundo y al momento se esfuman, durando sólo un suspiro. Las partículas virtuales tienen las mismas interacciones y las mismas cargas que las partículas físicas, pero disponen de energías que parecen estar mal. Por ejemplo, una partícula que se mueve muy rápido obviamente transporta mucha energía. Por el contrario, una partícula virtual puede tener una velocidad enorme y nada de energía. De hecho, las partículas virtuales pueden tener cualquier energía diferente de la energía que porta la correspondiente partícula física real. Si tuviera la misma energía, sería una partícula real, no una partícula virtual. Las partículas virtuales son un aspecto extraño de la mecánica cuántica que hay que tener en cuenta para llegar a las predicciones correctas.

¿Cómo pueden, entonces, existir estas partículas aparentemente imposibles? Una partícula virtual con su energía prestada no podría existir si no fuera por el principio de incertidumbre, que permite que las partículas tengan una energía incorrecta siempre y cuando esto ocurra durante un intervalo de tiempo tan corto que resulte imposible de medir.

El principio de incertidumbre nos dice que tardaríamos un tiempo infinito en medir la energía (o la masa) con una precisión infinita, y que cuanto más dura una partícula, más precisa puede ser nuestra evaluación de su energía. Pero si la partícula tiene una vida corta y no es posible determinar su energía con una precisión infinita, esa energía puede diferir temporalmente de la de una partícula auténtica de más larga vida. De hecho, a causa del principio de incertidumbre, las partículas harán todo aquello que puedan hacer sin que las pillen. Las partículas virtuales no tienen escrúpulos y hacen lo que les parece cuando nadie las mira. (Un físico de Ámsterdam llegó a insinuar que eran holandesas).

Podemos imaginar que el vacío es un depósito de energía: las partículas virtuales son partículas que surgen del vacío, tomando prestada temporalmente parte de su energía. Existen de un modo fugaz y desaparecen de nuevo en el vacío, llevándose la energía que tomaron prestada. Esta energía podría volver a su lugar de origen o podría ser transferida a partículas situadas en algún otro punto.

El vacío de la mecánica cuántica es un sitio muy frecuentado. Aunque por definición en el vacío no hay nada, los efectos cuánticos producen un mar hormigueante de partículas y antipartículas virtuales que aparecen y desaparecen, y, aunque no son estables, también las partículas de larga vida están allí presentes. Todas las parejas partícula-antipartícula pueden, en principio, producirse, aunque eso sí, sólo para visitas cortas; tan cortas que resulta imposible verlas directamente. Pero a pesar de lo breve de su existencia, hemos de ocuparnos de las partículas virtuales ya que, no obstante, dejan su marca en las interacciones de las partículas de larga vida.

Las partículas virtuales traen consecuencias mensurables porque ejercen su influencia sobre las interacciones de las partículas físicas reales que entran y salen de una determinada región de interacción. Durante el breve lapso de su existencia, una partícula virtual puede viajar entre partículas reales antes de desaparecer y de pagar su deuda de energía al vacío. Las partículas virtuales actúan por ello como intermediarios que ejercen su influencia sobre las interacciones de las partículas estables de larga vida.

Por ejemplo, el fotón de la figura 47, intercambiado para generar la fuerza electromagnética clásica, era, de hecho, un fotón virtual. No tenía la energía de un auténtico fotón, pero tampoco la necesitaba. Sólo precisaba durar lo suficiente como para comunicar la fuerza electromagnética y hacer interactuar las partículas cargadas reales.

En la figura 59 se muestra otro ejemplo de partículas virtuales. Aquí, un fotón entra en una región de interacción, se produce una pareja virtual electrón-positrón y luego la pareja es absorbida en otro punto. En el sitio donde son absorbidas las partículas, emerge del vacío otro fotón que se lleva la energía que la pareja intermedia electrón-positrón había tomado prestada temporalmente. Vamos a investigar ahora una consecuencia notable de este tipo de interacción.

FIGURA 59. Un fotón físico real puede convertirse en un electrón virtual y un positrón virtual, que, a su vez, pueden convertirse de nuevo en un fotón. Esto queda ilustrado a la derecha con un diagrama de Feynman y a la izquierda mediante un esquema.

Por qué la fuerza de interacción depende de la distancia

La intensidad de las fuerzas que conocemos depende de las energías y de las distancias que conciernen a las interacciones de las partículas, y las partículas virtuales desempeñan un papel en esta dependencia. Por ejemplo, la intensidad de la fuerza electromagnética es más pequeña cuando los dos electrones están más alejados entre sí. (Recuérdese que este decrecimiento propio de la mecánica cuántica se produce además de la dependencia clásica respecto a la distancia del electromagnetismo). Las consecuencias de las partículas virtuales y la dependencia en relación con la distancia de las fuerzas son reales; las predicciones teóricas y los experimentos concuerdan extraordinariamente bien.

La razón por la que las magnitudes de una teoría efectiva —la intensidad de las fuerzas o de las interacciones, por ejemplo— dependen de las energías y de la separación de las partículas implicadas resulta de una propiedad de la teoría cuántica de campos que el físico Jonathan Flynn llamó, con humor, el principio de anarquía.^[86] El principio de anarquía surge de la mecánica cuántica, que nos dice que todas las interacciones entre partículas que pueden darse de hecho se darán. En la teoría cuántica de campos, todo lo que no está prohibido ocurrirá.

A cada proceso independiente mediante el cual interactúa un grupo determinado de partículas voy a llamarlo un camino. Un camino puede o no implicar partículas virtuales. Cuando incluya alguna de éstas, diré que ese camino es una contribución cuántica. La mecánica cuántica nos dice que todos los posibles caminos contribuyen a la intensidad neta de una interacción. Por ejemplo, las partículas físicas pueden convertirse en partículas virtuales, que pueden interactuar entre sí y luego volver a convertirse en otras partículas físicas. En un proceso así, las partículas físicas originales podrían volver a emerger o podrían transformarse en otras partículas físicas diferentes. Aunque las partículas virtuales no durarían el tiempo suficiente como para que nos sea posible verlas directamente, afectarían de todos modos el modo de interacción entre las partículas observables reales.

Intentar evitar que las partículas virtuales faciliten una interacción sería como decir un secreto a unos amigos y esperar que aquél no llegue a oídos de otro amigo determinado. Sabemos que más tarde o más temprano alguno de los amigos «virtuales intermedios» traicionará nuestra confianza y transmitirá el mensaje al otro amigo. Aunque ya le hubiéramos dicho el secreto a este último, el hecho de que los amigos virtuales discutan también el secreto con él influirá asimismo en su opinión sobre el asunto. De hecho, su opinión será el resultado neto de todo lo que ha hablado con los demás.

No sólo las interacciones directas entre partículas físicas, sino también las interacciones indirectas, las que implican partículas virtuales, desempeñan su papel a la hora de transmitir una fuerza. Al igual que la opinión del amigo está influida por todo el que habla con él, la interacción neta entre partículas es la suma de todas las posibles contribuciones, incluidas las que provienen de las partículas virtuales. Y como la importancia de las partículas virtuales depende de las distancias implicadas, la intensidad de las fuerzas depende de la distancia.

El grupo de renormalización nos dice precisamente cómo calcular el impacto de las partículas virtuales en cualquier interacción. Todos los efectos de las partículas virtuales intermedias se van sumando, y esto refuerza o debilita las interacciones de un bosón gauge.

Las interacciones indirectas desempeñan un papel más importante cuando las partículas que interactúan entre sí están más separadas. Una distancia mayor es comparable al hecho de decir el secreto a más amigos «virtuales». Aunque uno no pueda estar seguro de que un amigo concreto vaya a traicionar la confianza puesta en él, cuantos más amigos sepan el secreto, mayor será la probabilidad de que alguno lo cuente. Siempre que exista un camino por el cual las partículas virtuales puedan contribuir a la intensidad neta de una interacción, la mecánica cuántica nos asegura que así lo harán. Y la aportación de las partículas virtuales que influye en esa intensidad depende de la distancia desde la que se transmite la fuerza.

Pero los cálculos reales del grupo de renormalización son todavía más astutos, ya que incorporan también las contribuciones de los amigos que hablan entre sí. Los caminos de un mensaje, a medida que va recorriendo los entresijos de una compleja burocracia, constituyen una analogía mejor de las contribuciones debidas a las partículas virtuales. Si una persona situada en la cima del escalafón envía un mensaje, éste llegará directamente. Pero alguien que se encuentre más abajo en el escalafón podría estar obligado a enviar previamente sus mensajes a los jefes, para que éstos los revisen. Si alguien que está en un nivel todavía más bajo envía un mensaje, quizá éste primero tenga que circular por más capas de papeleo antes de llegar, finalmente, a su destino. En este caso, en cada nivel los burócratas distribuirían el mensaje por su entorno antes de enviarlo a niveles más altos. El mensaje sólo se haría público una vez que hubiera alcanzado, finalmente, los escalones superiores. El mensaje que resultaría en este caso no sería, generalmente, igual que el original; por el contrario, sería el que quedaría después de haber sido filtrado a través de muchas capas de burocracia.

Si nos imaginamos que las partículas virtuales son burócratas y que un burócrata de nivel superior corresponde a una partícula virtual con más energía, un mensaje de alto nivel se comunicaría directamente, mientras que los de nivel inferior pasarían por muchas etapas. El vacío de la mecánica cuántica es la «burocracia» con la que se topa el fotón. Las partículas virtuales intermedias, que tienen cada vez menos energía, van siendo revisando cada interacción. Como en todo régimen burocrático, pueden producirse derivas en todos los niveles (o en todas las distancias). Algunos caminos sortearán los rodeos «burocráticos» impuestos por las partículas virtuales, mientras que otros habrán de contar con partículas virtuales que viajan a distancias cada vez más largas. Los contactos a más corta distancia (más alta energía) tropiezan con menos procesos virtuales que los que se producen a más larga distancia.

Sin embargo, hay una diferencia notable entre los procesos virtuales y un régimen burocrático. En un régimen burocrático, un mensaje determinado sigue un camino determinado, por muy complicado que éste sea. La mecánica cuántica, sin embargo, dice que puede haber muchos caminos. E insiste en que la intensidad neta de una interacción es la suma de las contribuciones de todos los posibles caminos que podrían recorrerse.

Consideremos un fotón que viaja de una partícula cargada a otra. Como puede convertirse en parejas de electrón-positrón sobre la marcha (véase la figura 60), la mecánica cuántica nos dice que algunas veces, efectivamente, así lo hará. Y las rutas con electrones y positrones virtuales debilitan la eficacia con la que el fotón transmite la fuerza electromagnética.

Y éste no es el único proceso cuántico que puede darse. Los electrones y los positrones virtuales mismos pueden emitir fotones, que pueden convertirse en otras partículas virtuales, y así sucesivamente. La distancia entre las dos partículas cargadas que intercambian el fotón determina cuántas interacciones de éstas tendrá el fotón mensajero con partículas en el vacío y cuán grande será el impacto de las interacciones. La intensidad de la fuerza electromagnética es el resultado neto de los muchos caminos que toma el fotón cuando se tienen en cuenta todos los rodeos burocráticos posibles, esto es, todos los procesos cuánticos en los que podrían participar partículas virtuales a distancias cortas o largas. Como el número de partículas virtuales que un fotón recorre depende de la distancia que recorre, la fuerza de interacción del fotón depende de la distancia entre los objetos cargados con los que interactúa.

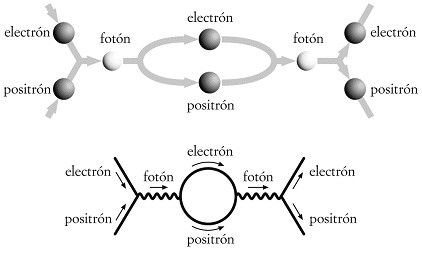
FIGURA 60. Corrección virtual de la dispersión electrón-positrón. Lectura de izquierda a derecha: un electrón y un positrón se anulan mutuamente y producen un fotón, que a su vez se escinde en una pareja virtual electrón-positrón, que entonces se anulan para dar un fotón, que a su vez se convierte en un electrón y un positrón. El electrón y el positrón virtuales intermedios debilitan así la intensidad de la fuerza electromagnética.

Cuando se suman todas las contribuciones de todos los posibles caminos, el cálculo muestra que el vacío diluye el mensaje que el fotón transmite de parte del electrón. La explicación intuitiva de la disolución de la interacción electromagnética es que las cargas opuestas se atraen y las cargas iguales se repelen, y por lo tanto, como promedio, los positrones virtuales están más próximos al electrón que los electrones virtuales. Las cargas de las partículas virtuales debilitan, por ende, el impacto pleno de la fuerza eléctrica del electrón inicial. Los efectos cuánticos tamizan la carga eléctrica. Este tamizado de la carga eléctrica implica que la intensidad de la interacción entre un fotón y un electrón decrece con la distancia.

La auténtica fuerza eléctrica a largas distancias parece ser más pequeña que la fuerza eléctrica clásica a cortas distancias porque un fotón que transmite una fuerza a corta distancia toma con más frecuencia un camino que no involucra partículas virtuales. Un fotón que viaje a corta distancia no tendría que pasar a través de una gran nube debilitadora de partículas virtuales, que es lo que debería hacer un fotón que transmitiera una fuerza a una gran distancia.

No sólo el fotón, sino todos los bosones gauge portadores de fuerza interactúan con las partículas virtuales en la marcha hacia su destino. Las parejas de partículas virtuales, la partícula y su antipartícula, surgen espontáneamente del vacío y son luego absorbidas por él, debilitando la intensidad neta de una interacción. Estas partículas virtuales abordan temporalmente al bosón gauge que transmite la fuerza y cambian la intensidad total de la interacción. Los cálculos prueban que la intensidad de la fuerza débil, así como la del electromagnetismo, decrece con la distancia.

Sin embargo, las partículas virtuales no siempre echan el freno a las interacciones. Sorprendentemente, a veces pueden también echarles una mano. A principios de la década de 1970, David Politzer, que entonces era estudiante de posgrado de Sidney Coleman (que fue el que propuso el problema) en Harvard, e independientemente David Gross y Frank Wilczek, discípulo suyo, por aquel entonces ambos en Princeton, y también Gerard ’t Hooft en Holanda, hicieron cálculos que probaban que la fuerza fuerte se comporta de un modo exactamente opuesto al de la fuerza eléctrica. Más que tamizar la fuerza fuerte a largas distancias y así debilitarla, las partículas virtuales en realidad acrecientan las interacciones de los gluones (las partículas que transmiten la fuerza fuerte), y tanto es así que la fuerza fuerte a largas distancias sigue mereciendo su nombre. Gross, Politzer y Wilczek ganaron el Premio Nobel de Física por sus penetrantes ideas sobre la fuerza fuerte.

La clave de este fenómeno está en los mismos gluones. Hay una gran diferencia entre los gluones y los fotones, y es que los gluones interactúan entre sí. Un gluón puede entrar en una región de interacción y convertirse en una pareja de gluones virtuales que afectan entonces a la intensidad de la fuerza. Estos gluones virtuales, como todas las partículas virtuales, existen sólo momentáneamente. Pero sus efectos se acumulan al aumentar la distancia, hasta que la fuerza fuerte es de verdad extraordinariamente fuerte. Y el resultado de un cálculo es que los gluones virtuales acrecientan de un modo drástico la intensidad de la fuerza fuerte cuando las partículas están más distantes. La fuerza fuerte es mucho más intensa cuando las partículas están bastante separadas que cuando están muy juntas.

Comparado con el tamizado que sufre la carga eléctrica, el incremento de la fuerza fuerte con la distancia es un resultado muy poco intuitivo. ¿Cómo puede ser que una interacción se haga más fuerte cuando las partículas están más separadas? La mayoría de las interacciones amainan con la distancia. En realidad, necesitaríamos un cálculo para probar esto que decimos, pero en el mundo hay ejemplos de comportamientos de este tipo.

Por ejemplo, si alguien envía a través de un régimen burocrático un mensaje cuya importancia no comprende algún directivo intermedio, éste podría inflar lo que de otro modo no hubiera sido sino un memorándum más y convertirlo en una directriz de importancia capital. Una vez modificado el mensaje por el directivo intermedio, aquél tendrá un impacto muchísimo mayor que si hubiera sido comunicado directamente por el autor original.

La guerra de Troya es otro ejemplo en el que las fuerzas fueron más poderosas a larga que a corta distancia. Según la Ilíada, la guerra de Troya empezó cuando el príncipe troyano Paris decidió huir con Helena, la mujer de Menelao, rey de Esparta. Si Menelao y Paris hubieran peleado por Helena mano a mano antes de que estos últimos se fugaran a Troya, la guerra entre los griegos y los troyanos hubiera concluido sin llegar a convertirse en una epopeya. Cuando Menelao y Paris estuvieron lejos el uno del otro, ambos interactuaron con muchas personas y crearon las intensas fuerzas que participaron en las poderosísimas interacciones entre griegos y troyanos.

Aunque sorprendente, el crecimiento de las interacciones fuertes con la distancia es suficiente para explicar todas las propiedades características de la fuerza fuerte. Explica por qué la fuerza fuerte tiene la fuerza suficiente para mantener a los quarks empaquetados, formando protones y neutrones, y atrapados en los flujos: la fuerza fuerte aumenta tanto a larga distancia que una partícula que la experimenta no puede separarse demasiado de otras partículas con interacciones fuertes. Las partículas fundamentales con interacciones fuertes como los quarks nunca se encuentran aisladas.

Un quark y un antiquark muy separados acopiarían una enorme cantidad de energía, tanta que sería mucho más eficiente desde el punto de vista energético crear nuevos quarks y antiquarks físicos entre ellos que permitir que siguieran aislados. Si intentáramos separar todavía más el quark y el antiquark, se crearían del vacío nuevos quarks y antiquarks. Tal como sucede con el tráfico de Boston, donde uno no puede separarse mucho del coche que le precede sin que se le cuele un coche que surge de una bocacalle, esos nuevos quarks y antiquarks rondarían alrededor de los originales, de modo que ningún quark ni ningún antiquark individual estaría más aislado que al principio: siempre habría cerca de él otro quark u otro antiquark.

Como la fuerza fuerte a largas distancias es tan intensa que no permite a las partículas con interacciones fuertes permanecer aisladas entre sí, las partículas cargadas con la fuerza fuerte se encuentran siempre rodeadas por otras partículas cargadas, formando configuraciones de carga fuerte nula. Como consecuencia, nunca vemos quarks aislados. Sólo vemos hadrones fuertemente cohesionados y flujos.

La gran unificación

Los resultados de la sección anterior nos hablan de cómo dependen de la distancia las fuerzas fuerte, débil y electromagnética.^[M21] En 1974, Georgi y Glashow insinuaron con atrevimiento que estas tres fuerzas cambian en función de la distancia y de la energía, de manera que resultan unificadas como una única fuerza a altas energías. A esta teoría la llamaron una gran teoría unificada (GUT, según sus siglas en inglés). Mientras que la simetría de la fuerza fuerte intercambia tres colores de quarks (como se discutió en el capítulo 7) y la simetría de la fuerza débil intercambia diferentes parejas de partículas, la simetría de la fuerza de la GUT actúa sobre todos los tipos de partículas del modelo estándar, quarks y leptones, y los intercambia.^[M22]

Según la gran teoría unificada de Georgi y Glashow, en los primeros tiempos de la evolución del universo, cuando la temperatura y la energía eran enormemente altas —la temperatura era superior a los cien billones de billones de grados Kelvin y la energía superior a mil billones de GeV—, la intensidad de cada una de las tres fuerzas era la misma y las tres fuerzas no gravitatorias estaban fundidas en una única fuerza, «La Fuerza».

Al evolucionar el universo, la temperatura bajó y la fuerza unificada se escindió en tres fuerzas distintas, cada una con una dependencia diferente con respecto a la energía, a través de la cual evolucionaron hacia las tres fuerzas no gravitatorias que conocemos hoy. Aunque las fuerzas empezaron como una sola fuerza, acabaron con intensidades de interacción muy diferentes a bajas energías a causa de las distintas influencias que las partículas virtuales ejercieron sobre cada una de ellas.

Las tres fuerzas serían como trillizos idénticos que se desarrollaran a partir de un único huevo fertilizado, pero que maduraran para producir tres individuos bastante diferentes. Uno de los trillizos podría ser ahora un cantante punk con una cresta de pelo teñido, otro un marine con el pelo rapado y el tercero un artista con una larga coleta. Compartirían, de todos modos, el mismo ADN y, de bebés, habrían sido casi indistinguibles.

En los primeros tiempos del universo, las tres fuerzas habrían sido también indistinguibles. Pero luego se habrían diferenciado mediante la ruptura espontánea de la simetría. Así como el mecanismo de Higgs rompió la simetría electrodébil y sólo dejó intacto el electromagnetismo, rompería también la simetría de la GUT y dejaría las tres fuerzas independientes que vemos hoy.

Una única intensidad de interacción a altas energías es un prerrequisito para una gran teoría unificada. Esto implica que las tres líneas que representan la intensidad de interacción como función de la energía deben coincidir a partir de un valor dado de la energía. Pero ya sabemos cómo varía la intensidad de las tres fuerzas no gravitatorias en función de la energía. Y como la mecánica cuántica nos dice que una distancia larga equivale a una energía baja y que una distancia corta equivale a una energía alta,^[87] los resultados de la sección anterior pueden interpretarse igualmente en términos de la energía. A bajas energías, las fuerzas electromagnética y débil son menos potentes que la fuerza fuerte, pero se intensifican a energías más altas, mientras que la fuerza fuerte se debilita.

En otras palabras, las intensidades de las tres fuerzas no gravitatorias se van haciendo más equiparables a energías más altas. Podrían incluso converger hacia una intensidad común. Esto significaría que las tres líneas que representan la intensidad de interacción en función de la energía coinciden a altas energías.

Dos líneas que se encuentran en un punto no es un resultado tan fascinante: eso va a ocurrir de todos modos si las dos líneas se van aproximando. Pero que tres líneas se encuentren en un punto es una gran coincidencia o la prueba de algo más significativo. Si es verdad que las fuerzas convergen, su intensidad de interacción común podría ser una indicación de que hay sólo un único tipo de fuerza a altas energías, y en ese caso tendríamos una teoría unificada.

Aunque la unificación sigue siendo hasta hoy una conjetura, la unificación de las fuerzas, si fuera cierta, sería un gran salto hacia una descripción más sencilla de la naturaleza. Al ser los principios de unificación tan intrigantes, los físicos estudiaron la intensidad de las tres fuerzas a altas energías para ver si convergen o no. Hacia 1974, nadie había calculado la intensidad de interacción de las tres fuerzas no gravitatorias con una gran precisión. Howard Georgi, Steven Weinberg y Helen Quinn (por aquel entonces, ayudante postdoctoral sin sueldo en Harvard, y, actualmente, física de plantilla en el Acelerador Lineal de Stanford y presidenta de la Sociedad Americana de Física) usaron las mediciones imperfectas que estaban entonces disponibles e hicieron un cálculo con el grupo de renormalización para extrapolar la intensidad de las fuerzas a altas energías. Descubrieron que las tres líneas que representan la intensidad de las fuerzas no gravitatorias parecían realmente convergir en un único punto.

El famoso artículo de Georgi y Glashow de 1974 sobre su teoría de la gran unificación comienza con estas palabras: «Presentamos una serie de hipótesis y de especulaciones que conducen sin remedio a la conclusión […] de que todas las fuerzas producidas por partículas elementales (la fuerte, la débil y la electromagnética) son diferentes manifestaciones de la misma interacción fundamental que involucra a una única intensidad de conexión. Nuestras hipótesis pueden ser erróneas y nuestras especulaciones absurdas, pero la unidad y la sencillez de nuestro esquema son razones suficientes para que sea tomado en serio».^[88] Quizá aquellas palabras no eran demasiado modestas. Sin embargo, Georgi y Glashow no pensaban realmente que la unidad y la sencillez constituyeran pruebas suficientes de que su teoría fuera una descripción correcta de la naturaleza. También querían que hubiera una confirmación experimental.

Aunque era preciso un tremendo acto de fe para extrapolar el modelo estándar a una energía diez billones de veces más grande que la que había sido explorada directamente hasta entonces, se dieron cuenta de que esa extrapolación tenía una consecuencia verificable. En su artículo, Georgi y Glashow explicaron que su GUT, su teoría de la gran unificación, «predice que el protón se desintegra» y que los físicos experimentales deberían intentar comprobar esta predicción.

La teoría unificada de Georgi y Glashow predecía que los protones no durarían siempre. Después de mucho tiempo, se desintegrarían. Esto no pasaría nunca en el modelo estándar. Los quarks y los leptones se distinguen normalmente entre sí por las fuerzas que experimentan. Pero en una gran teoría unificada, las fuerzas son todas esencialmente una misma fuerza. Así, al igual que un quark up puede convertirse en un quark down por efecto de la fuerza débil, un quark podría convertirse en un leptón por efecto de la fuerza unificada. Esto implica que, si la idea de la gran teoría unificada es correcta, el número total de quarks del universo no sería fijo y un quark podría convertirse en un leptón, haciendo que el protón, que está compuesto de tres quarks, se desintegre.

Como el protón puede desintegrarse en una gran teoría unificada que vincula los quarks a los leptones, toda la materia familiar sería, en definitiva, inestable. Sin embargo, la tasa de desintegración del protón es lentísima: su tiempo de vida superaría ampliamente la edad del universo. Esto implica que la señal de un protón que se desintegra, por vistosa que sea, tiene poquísimas posibilidades de ser detectada, ya que se produce muy rara vez.

Para encontrar pruebas de la desintegración del protón, los físicos tuvieron que diseñar experimentos en extremo complicados y de larga duración, que estudiaron una enorme cantidad de protones. De este modo, aunque es muy poco probable que cualquier protón concreto se desintegre, un gran número de protones incrementa mucho la posibilidad de que el experimento pueda detectar la desintegración de uno de ellos. Aunque la probabilidad de que nos toque la lotería es pequeña, sería mucho mayor si compráramos millones de billetes.

Los físicos diseñaron ciertamente este tipo de experimentos, complicados y a base de muchos protones; entre ellos está el proyecto Irvine/Michigan/Brookhaven (IMB), localizado en la mina Homestake, en Dakota del Sur, y el proyecto Kamiokande, una tina de agua y de detectores enterrados a un kilómetro de profundidad en Kamioka, Japón. Aunque la desintegración del protón es un proceso rarísimo, estos experimentos ya hubieran encontrado pruebas de él si la teoría de la gran unificación de Georgi y Glashow fuera correcta. Por desgracia para las ambiciones de la gran unificación, nadie ha descubierto hasta ahora esa desintegración.

Esto no descarta necesariamente la unificación. De hecho, gracias a medidas más precisas de las fuerzas, ahora sabemos que el modelo original propuesto por Georgi y Glashow es, casi con certeza, incorrecto, y que sólo una versión ampliada del modelo estándar puede unificar las fuerzas. Resulta que en esos modelos las predicciones sobre la vida del protón son más largas y por eso resultaría lógico que la desintegración del protón no haya sido detectada aún.

Todavía hoy no sabemos realmente si la unificación de las fuerzas es una verdadera propiedad de la naturaleza, y si es así, qué significa eso. Los cálculos muestran que la unificación podría darse en varios modelos que explicaré más adelante, entre los que se encuentran los modelos supersimétricos, los modelos extradimensionales de Hořava y Witten y los modelos extradimensionales arqueados que desarrollamos Raman Sundrum y yo. Los modelos extradimensionales son particularmente intrigantes porque podrían llevar a la gravedad al redil de la unificación y unificar de verdad las cuatro fuerzas conocidas. Estos modelos son también importantes porque en los modelos originales de unificación se suponía que no había nuevas partículas por descubrir que estuvieran por encima de la escala débil y que no fueran las que tienen masa en la escala de la teoría de la gran unificación.^[89] Estos otros modelos demuestran que la unificación podría darse aunque hubiera muchas otras partículas que pudieran producirse solamente a energías que están por encima de la escala débil.

Sin embargo, por fascinante que pueda ser la unificación de las fuerzas, los físicos se encuentran actualmente divididos sobre sus méritos teóricos, según propugnen un planteamiento de la física que vaya de arriba hacia abajo o uno que vaya de abajo hacia arriba. La idea de una teoría de la gran unificación encarna el planteamiento que va de arriba hacia abajo. Georgi y Glashow formularon una atrevida hipótesis sobre la ausencia de partículas con masa entre mil y mil billones de GeV y desarrollaron una teoría hipotética basada en esta suposición. La gran unificación fue el primer paso del debate de la física de partículas que continúa hoy con la teoría de cuerdas. Ambas teorías extrapolan las leyes físicas desde las energías efectivamente medidas hasta energías por lo menos diez billones de veces superiores. Georgi y Glashow se volvieron después escépticos sobre el planteamiento que va de arriba hacia abajo, que está representado por la teoría de cuerdas y por la búsqueda de la gran unificación. Desde entonces han vuelto sobre sus pasos y ahora se concentran en la física de bajas energías.

Aunque las teorías unificadas tienen algunos rasgos atractivos, no estoy realmente segura de que con su estudio se llegará a ideas correctas sobre la naturaleza. El intervalo de energías que hay entre lo que sabemos y lo que extrapolamos es enorme, y podemos imaginar muchas posibilidades para lo que puede ocurrir a medio camino. En todo caso, hasta que se descubra la desintegración del protón (o alguna otra predicción), si es que esto ocurre alguna vez, será imposible establecer con certeza si las fuerzas de verdad se unifican a altas energías. Hasta entonces, esta teoría permanecerá en el reino de las especulaciones grandiosas, pero teóricas.