Archimedes parabolakvadraturája

A nagy Archimedes kétségtelen érdeme, hogy görbevonalú idomok kvadraturájára olyan zseniális módszereket gondolt ki, hogy ezek a XVII. század végéig hatással voltak a matematika fejlődésére és általánosan alkalmazták őket. Éppen ezért nem resteljük a fáradságot és kissé mélyebben megismerkedünk Archimedes idevágó gondolataival. Evégből a két értekezésben is tárgyalt parabolakvadraturát fogjuk megismerni. Az ő geometriai okoskodásait vesszük elő és mellőzzük a számunkra nehezebb statikai módszert.

Archimedes geometriai módszere, az úgynevezett exhaustio, vagyis kimerítés; már szóltunk róla. Lényege, hogy könnyen kezelhető, egyenes vonalú idomokat ír bele az illető görbevonalú idomba. Ha végnélkül szaporítjuk a beírt idomok számát, úgyhogy valamennyi végnélkül kisebbedjék : végnélkül simulnak az egymásutáni egyenesvonalú idomok a görbevonalúhoz, mindaddig, amíg végtelen sok ismétlés után olyan egyenesvonalú idomhoz érkezünk, amelynek határvonalai a görbe ívelemeinek tekinthetők. Most kell a második, lényeges lépést megtennünk: összegeznünk kell a végtelen sok, egyenessel határolt idomot, mert ez az összeg adja a «kimerített», a végtelen sok, hasonló idommal megtöltött, görbevonalú idom területét. Hogy ez részleteiben miként történik, azt később látjuk meg. Most azonban vegyük fel a "közönséges parabola" tetszésszerinti darabját. E parabolának számos tulajdonsága már Archimedes idejében ismeretes volt.

Határozzuk meg tehát egy úgynevezett parabolaszelet, azaz parabolaszegmens területét. (Szegmens, mint tudjak, a szelet neve, a szektor viszont a cikknek a megfelelője. A kezdő gondoljon a szegmens hallatán egy kerek kenyérből levágott részre, a szektor viszont köralakú tortából szokott módon kivágott részt jelent.) Rajzoljunk ebbe a szeletbe háromszöget Olymódon, hogy csúcsa a parabolának úgynevezett csúcsával essék egybe és e csúccsal szemben fekvő oldala a parabola tengelyére merőleges legyen. Egyszerűség kedvéért, — hisz a parabola szimmetrikus a tengelyére, — s a későbbi, integrálással történő területmeghatározással való könnyebb összehasonlítás kedvéért, a parabolaszeletnek csak a felső felét vesszük tekintetbe. Ebben a részben most egy nagy, derékszögű háromszög van, átfogója a parabolának úgynevezett csúcsától a szeletet határoló húrnak és a parabolának metszéspontjáig terjed. E háromszögnek, amelyet a következőkben «a nagy háromszög»-nek fogunk nevezni, egyik befogója a parabola tengelye, a másik pedig egy arra merőleges S egyenes, amely nem egyéb, mint az imént említett húrnak a fele.

Fogjunk már most neki az exhaustionak, a kimerítésnek. Evégre a nagy háromszög átfogójára mint alapra új, (az 53. ábrán vonalkázott) háromszöget rajzolunk, de ez már természetesen nem derékszögű. A vonalkázott háromszög két oldalára mint alapra ismét egy-egy, a képen fekete, háromszöget helyezünk. E fekete háromszögek harmadik csúcsa, miként minden eddigi háromszögé, a parabolán van. Most már gondolatban tovább is folytathatjuk ezt az eljárást. A fekete háromszögek két-két szabad oldalára ismét egy-egy, még kisebb, háromszöget gondolhatunk, csúcsaik természetesen ismét a parabolán vannak és így tovább a végtelenségig. Mindenki belátja, hogy a háromszögek sorozata kitölti a fél parabolaszegmenst. De hogyan tudjuk összegezni e végtelen sok háromszöget?

Az erre adott felelet teljes fényében mutatja a régi görögök matematikai lángeszét. S megcsodálhatjuk azt a szinte hihetetlenül egyszerű és világos módot, amellyel Archimedes ezt a látszólag megoldhatatlan problémát elintézte. Tudta ugyanis, hogy olyan fogyó végtelen sorok összege meghatározható, amelyekben a tagok viszonya állandó. Tudta tehát, hogy pl. az 1+1/2+1/4+1/8... sor összege véges, mégpedig = 2. Ha tehát sikerül a szemmel láthatóan kisebbedő háromszögek csökkenését valamely állandó viszonyszámmal ki fejezni, akkor az egész feladatot fogyó végtelen sorok összegezésére vezettük vissza. A nagy háromszög bármekkora lehet, egyszerűen egységnek tekintjük és a többi háromszög területét ebben az egységben fejezzük ki. Azután, ha az összegezés megtörtént, az eredményt megszorozhatjuk a nagy háromszög valódi területével, s ebből azonnal megkapjuk a parabolaszelet területét.

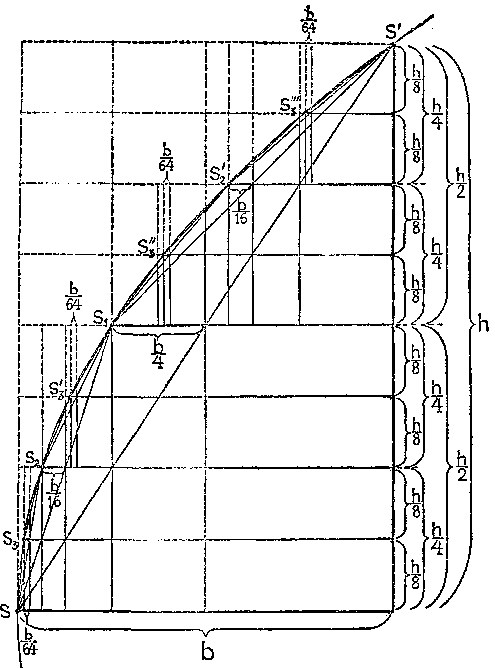
Archimedes valóban elérte ezt a célt. Az ő gondolatmenetét fogjuk követni, némiképpen egyszerűsített, de lényegében változatlan módon. Jó szolgálatot tesz majd eközben az 54. ábra vázlatos rajza. Előrebocsátjuk, hogy a parabolának igen sajátos tulajdonságai vannak, de ezek bizonyítása túlságosan messze vezetne. Tehát csak annyit említsünk, hogy azokat a vízszintes, párhuzamos egyeneseket, amelyek a parabolát az S, S₃, S₂, S₃ stb. pontban metszik, a parabola átmérőinek nevezzük. Égy ilyen átmérő akkor felezi a metszett parabola-húrt, ha az átmérőnek a húr és az ív közé eső része a leghosszabb átmérődarab az illető húr által levágott szeletben. Ez esetben az átmérőnek és a parabolának metszéspontját az illető szelet csúcsának is nevezik. Így S₁ a csúcsa az SS' húr által levágott szeletnek, S₂ az S és S₁ közötti szeleté, S₃"' pedig az S₂' és S' közöttié stb. Említsük még, hogy a régi görögök, így Archimedes is tudták, hogy a b tengelydarab úgy viszonylik valamely részéhez, mint h² viszonylik az illető rész végpontjában emelt merőleges tengely és parabola közötti részének négyzetéhez. Mai matematikai nyelvünkön ez azt jelenti, hogy a parabolának analitikus jelöléssel írt egyenlete y² = x, vagy y = gyök(x).

De most foglalkozzunk magával a problémánkkal.

A nagy háromszögnek itt (54. ábra) b és h a befogói, átfogója pedig az SS' húr. Területe ezek szerint bh/2. Húzzunk a végpontján keresztül átmérőt, akkor ismét új, az SS'S₁ szelethez tartozó S₁ parabolacsúcshoz jutunk. Az

ebbe a szeletbe beírt SS'S₁ háromszöget a távolság két részre osztja, a két rész alapja közös, magasságuk pedig egyformán h/2. Területük együttvéve 2(b/4*h/2) : 2. Ez azt jelenti, hogy bh/8 az SS’S₁ háromszög területe. Az előző

ábra kifejezéseivel élve azt mondhatnánk, hogy a nagy háromszög területe négyszer akkora, mint a vonalkázott háromszögé.

Húzzunk most további két átmérőt h/4 -nél és 3h/4-nél, vagyis a két h/2-t ismét megfelezzük. Az osztópontokon keresztül húzott átmérők ismét csúcspontokat adnak, az S₂ és S'₂ pontokat.

Az új SS₁S₂ és S₁S₂'S' szegmensekbe újból háromszögeket rajzolunk. Ezeket a háromszögeket neveztük előbb "fekete háromszögeknek", s a parabola tulajdonságai alapján megismétlődik az előbbi játék változott méretekkel. Négy b/16-alapú háromszögünk van most, kettő-kettő együtt egy-egy fekete háromszöget ad. Mindegyik részháromszögnek (b/16*h/4) : 2 a területe, tehát a négyé együtt (4bh/64) : 2. Vagyis bh/32.

De ez azt jelenti, hogy a két "fekete háromszög" területe együtt a vonalkázott háromszögek területének negyede. Ugyanezt a képzési törvényt újból alkalmazva megfelezzük az ábrán látható darabokat, akkor négy új átmérő négy új csúcspontot ad: S₃, S₃', S₃", S₃"'. A négy exhaustiós háromszög nyolc b/64 alapú háromszögre bontható. Magasságuk h/8 összes területük tehát 8*(b/64*h/8) : 2 = De ez megint nem jelent mást, mint hogy új háromszögeink területe negyede az előbbi két fekete háromszög területének. Nem merülünk ábránkról leolvasható további nagyon változatos törvényszerűségek ismertetésébe, csupán a számunkra jelentős tanulságokat foglaljuk össze. Azt tapasztaltuk, hogy eljárásunk; h felezése, átmérő rajzolás, háromszögszerkesztés, fogyó sort szolgáltat. Ezt a sort egyelőre csak szavakba foglalva írjuk le. A nagy háromszög négyszer akkora, mint a vonalkázott. A vonalkázott a két feketének négyszerese. A két fekete négyszerese annak a négy háromszögnek, amelyek csúcsai sorban S₃, S'₃, S₃", S₃"' és így tovább a végtelenségig. Ha most a nagy háromszöget tekintjük egységnek, akkor a parabolaszelet területét a következő sor szolgáltatja : Parabolaszelet területe = 1 + 1/4+1/16+1/64 +...., minthogy ebben a sorban minden tag a megelőzőnek negyede. Most már csak a sor összegét kell a nagy háromszög területével, a korábbiak szerint, megszoroznunk, hogy a parabolaszelet területét megkapjuk. Tehát a végeredmény:

Parabolaszelet = nagy háromszög * (l + 1/4 + 1/16 + 1/64 + ...)

Most már csak az van hátra, hogy a végtelen sok tagból álló fogyó sor összegét meghatározzuk. Elébevágunk tanulmányainknak, de eláruljuk, hogy az összeget az S_∞ = a/1-q képlettel kell meghatározni. A képletben a a kezdő tagot jelenti, q a hányadost, a kvocienst. Esetünkben a kezdő tag 1,

a hányados 1/4, tehát

Ezzel mindent tudunk. A parabolaszelet területe a nagy háromszög területének pontosan négyharmada. Ha ábránkat a szaggatott vonalakkal kiegészítve tekintjük, akkor egy derékszögű négyszög áll előttünk, oldalai b és h, területe pedig a nagy háromszög területének kétszerese. Területe tehát a nagy háromszöggel mint egységgel mérve 2. Ha végül a parabolaszelet és a négyszög területét hasonlítjuk össze, akkor kiderül, hogy a kettőnek a viszonya 4/3 : 2 = 2/3. Ez azt jelenti, hogy a parabolaszelet területe kétharmada a húr feléből és a tengely metszetéből alkotott négyszögnek. (Helyesen, az analízis kifejezéseivel, azt is mondhatnánk, hogy a parabolaszelet területe ama pont koordinátáiból alkotott négyszög területének kétharmada, amelyben a húr a parabolát metszi.) Mielőtt még a klasszikus görög geometria érdekes területét elhagynánk, meg kell említenünk, hogy az első háromszögnek egyáltalán nem kellett derékszögűnek lennie. Kiindulásul valamely ferdén levágott szeletet, így például a vonalkázott háromszöget és a hozzá tartozó szeletet is választhattuk volna. Sőt ez a választás helyesebb is, mert általánosabb. Ha így választunk, akkor azt találjuk, hogy valamely ferdeszögű parallelogramma két átellenes csúcsán keresztülmenő parabola a parallelogrammát 1/3 : 2/3 arányban osztja két részre. Továbbá, hogy az exhaustiós háromszögek területének összege mindenkor egyharmada a kiindulásul választott háromszög területének. Mi a derékszögű esetet csak a levezetés és demonstrálás egyszerűsítése céljából választottuk, valamint azért, hogy a későbbi tanulmányaink folyamán integrálszámítással végzett területmeghatározást példánkkal könnyebben összehasonlíthassuk.

HARMINCADIK FEJEZET

Sorok

Most azonban újra a sorok elméletéhez kell fordulnunk és hozzácsatoljuk még a soroknál levő egy másik különbség rövid megemlítését. Vannak sorok, amelyek additív nőnek vagy szubtraktív fogynak. Például

1±3±5±7±9± .... és így tovább

vagy

500±496±492±488± ... és így tovább.

Az első sor tagonként 2-vel nő, a második 4-gyel fogy. Az ilyen sorokat számtaniaknak nevezik. Ha ellenben a sorok szorzás által nőnek és a legközelebbi tagot úgy kapjuk, hogy az adott tagot egy mindig ugyanaz maradó tényezővel szorozzuk (vagy egy állandó osztóval osztjuk), akkor egy mértani sorról beszélünk. Például:

1±3±9±27±81± és így tovább

vagy

1 ± 1/4 ± 1/16 ± 1/256 ± ... és így tovább.

Általában írva így hangzik a számtani sor: a+(a+d) + (a+2d)(a+3d) ± ... ± (a+nd)

vagy

a±(a-d)±(a—2d)±(a—3d)± ... ±(a—nd),

a mértani ellenben:

a±aq±aq²±aq³± ... ± aq^n-1

vagy

Itt is eltekintünk a levezetésektől és csak megemlítjük, hogy e sorokat «progressziók»-nak is szokás nevezni és hogy az a-t, ami természetesen egyáltalán nem kell 1 legyen, «kezdőtag»-nak nevezik. A számtani progresszióknál a növekedési vagy kisebbedési szám d a «differencia», a mértani progresszióknál a q-t vagy az 1/p -t «kvociens»-nek nevezik.

Minket elsősorban egy ilyen sor összege érdekel. Számtani soroknál, ha a kezdőtag a, a differencia d és a tagok száma n, akkor az összegképlet

Számtani sorok végtelen összege nem lehetséges, ami azt teszi, hogy ezek mind végtelent adnak összegül, tehát minden számtani sor divergens. Következőleg az n-t mindig véges számként kell megadni, ha értelmes feladatot akarunk felállítani. Számítsuk ki például az első 9 páros szám összeget, tehát

2+4+6+8+10+12+14+16+18=?

A kezdőtag a=2, a differencia d=2 és a tagok száma n=9. Tehát

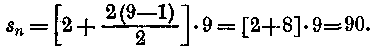
ami képletünket kitűnően igazolja.

A mértani progressziókra nézve érvényes az összegképlet:

Tehát ha keresnénk a

3+15+45+ ...

progresszió első 6 tagjának az összegét, akkor tudnánk, hogy a=3, g=5 és n=6. Tehát:

ami a

8+15+75+375+1875+9375=11718

összeadással könnyen ellenőrizhető.

Most egyszer egy oly mértani progressziót akarunk megvizsgálni, amelynek «kvociense» tört, Utalunk arra, hogy éppen ezek a mértani sorok, amelyek mindegyre fogynak és ezért voltaképp nem "progresszióknak", hanem (degresszióknak» volnának nevezhetők, az egész matematikában rendkívüli szerepet játszanak. Általánosan írva n tagszám esetén ily alaknak:

Azok után, amiket eddig hallottunk, a sorok eme fajtájánál is lehet értelme végtelen sok tag összege után kérdezősködni. Felállítjuk ezért a problémát, hogy mely határértékhez «konvergál» egy ily sor, mely összeghez tart. Egy

ily sorra nézve áll a képlet

ahol itt q-t tettünk egyszerűségért 1/p helyébe azért, hogy ne kapjunk törtestörtet (kettőstörtet). Tehát írhatjuk

ami nem mást jelent, mint hogy itt a «kvociens» valódi tört. Eme képlettel először a parabolaszeletre vonatkozó Archimedes-féle sort akarjuk megvizsgálni. Ennek alakja

1+1/4+1/16+1/64+1/256+1/1024+ ...

Itt az a kezdőtag 1-gyel egyenlő. A «kvociens» 1/4, mivel minden következő tag egynegyede a megelőzőnek (vagy minden tagot 1/4-del kell megszorozni, hogy a legközelebbi tag adódjék). Az összegnek tehát végtelen sok tag esetén az

értékhez kell konvergálni.

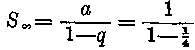
Ámde

egyenlőa mit már előbb mint eredményt állítottunk oda. Ha például az

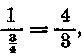
1+1/2+1/4+1/8 + ...

sor volna előttünk, akkor most rögtön tudnánk, hogy végtelen összege

Egy másik sor 1/3+1/9+1/27+1/82+... végtelen összege ellenben

Általánosan a mi képletünk alkalmazásával állítható, hogy az |x| < 1 feltétel mellett bármely l+x+x²+x³+x⁴+x⁵+... alakú végtelen sor összege 1/1-x, ami hasonlóképp messzehordó jelentőségű.

Már e néhány példából eljutunk annak a belátásához, hogy konvergens sorok végtelen összegének a kiszámításában egy határozott infinitézimális elv rejlik, amely lehetővé teszi mindenféle geometriai probléma megoldását. Például mihelyt képesek vagyunk valamely idomot — mégha görbevonalú határa is van — oly végtelen sok idomra bontani szét, amelyek területei fogyó mértani sorba rendezhetők, akkor a kvadratura integrálszámítás nélkül is elvégezhető. Egy ilyenféle példát már Archimedesnél láttunk. És nincs jogunk lekicsinyelni Archimedes utolsó tanítványainál — mint például egy Galileinél vagy Vivianinál — azt a roppant éleselméjűséget, amely az exhaustio módszerében egyenesen hihetetlent végzett. Ezen természetesen mit sem változtat az, hogy éppen Vivianinak, a nagy Leibniz barátjának, kellett át szenvednie annak tragikumát, hogy alkotásának a tetőpontján a matematikai trónról menthetetlenül letaszította és fáradozásának minden gyümölcsét elvette az infinitézimális számítás csodája. Mi epigonok azonban most véglegesen birtokunkba akarjuk venni az érett gyümölcsöket.

HARMINCEGYEDIK FEJEZET.