A kvadratura problémája
Minden olvasó hallott már bizonyára valamilyen összefüggésben a kör négyszögesítéséről. S azt is hallotta, hogy ez épp úgy megoldhatatlan, mint a perpetuum mobile szerkesztése.
Mit nevezünk négyszögesítésnek, kvadraturának? Nos, ez lényegében nem más, mint területmérés. Mert a feladat vagy azt kívánja, hogy bontsunk egy kört négyzetegységekre, alakítsuk ilyen négyzetek összegévé, tehát mondjuk meg, hogy területe hány négyzetegység (mondjuk négyzetmilliméter), vagy pedig azt, ami lényegében úgy sem más, hogy ábrázoljuk olyan négyzettel, amelynek területe éppen a kör területével azonos. Már régebben is sejtették, de csak a múlt század nyolcvanas éveiben bizonyította be Lindemann, hogy ez a feladat megoldhatatlan, bármilyen kicsiny egységet választok is.
A π szám tehát végtelen tizedestört, jellegre nézve irracionális, s tekintve, hogy a kör területe mindenkor r2π, úgy racionális r esetén a terület csak irracionális lehet. Ilyen számot azonban soha sem lehet mérésre használt négyzetekkel ábrázolni, mert utóbbiak méretét végtelen kicsinek kellene választanunk, hogy ne maradjon a területből semmi.
De már a nagy Archimedes is tudta, hogy a körnél bonyolultabb idomok is léteznek, s még sincs területük kifejezésére irracionális számra szükségünk. S nehéz elképzelni,- hogy miért volna lehetetlen, hogy valamely görbe vonalakkal határolt idom területe történetesen racionális számú terület-egységgel egyenlő. Sőt ezt még igen észszerű bizonyítékokkal is alá lehet támasztani. Ha nagyon egyenletes vastagságú kartonból kivágunk egy négyzetet, mondjuk olyat, amelyiknek oldala 1 centiméter, súlyát precíziós mérlegen lemérjük és kerekszámban 3/10 grammnak találjuk, akkor feltétlenül lehetséges ugyanabból a kartonból, kellő gondossággal, pontosan 8 gramm súlyú, de görbe vonalakkal határolt idomot kivágni. Az idom területe ekkor biztosan 80 négyzetcentiméter. Irracionális számokról nincs is szó.
Ilyen megfontolásokon kívül sok gondot okoztak a görög matematikusoknak például a «keosi Hippokrates holdjai». Kvadraturájuk Pythagoras tételének általánosításán alapul. Már az ókorban bebizonyították, hogy nem csak a befogók fölé rajzolt négyzetek területének összege egyenlő az átfogón rajzolt négyzet területével, hanem általában az is igaz, hogy a befogók fölé rajzolt hasonló idomok területének összege egyenlő a hozzájuk hasonló és az átfogóra rajzolt idom területével. Mellékesen ez az általánosított Pythagoras tétel a "szamarak hídjának" igen egyszerű és szellemes bizonyítására is alkalmas.

42. ábra.
A 42. ábrán látható derékszögű háromszöget a magasság két, hasonló, részháromszögre bontja. Hasonlók, mert megfelelő szögeik egyenlők. A két háromszög a befogók fölé rajzolt hasonló idomnak tekinthető, habár befelé rajzoltuk őket. Az egész háromszög a szögek azonossága következtében szintén hasonló a részháromszögekhez, s az "átfogóra rajzolt hasonló idomnak" is tekinthető. Ebből az általánosított Pythagoras tétel helyessége szembeötlő világossággal mutatkozik. A befogóhoz tartozó háromszögek összege ugyanis nem egyéb, mint maga az "átfogóra rajzolt háromszög".
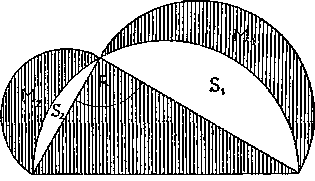
43. ábra.
Az általánosított Pythagoras tétel alapján az átfogóra rajzolt félkör területe is egyenlő a befogóra rajzolt félkörök területének összegével. A félkörök ugyanis mindig egymáshoz hasonló idomok. Mivel ábránkon az átfogóra rajzolt félkör a háromszög és a fehér S1 és S2 szegmensek területéből tevődik össze, továbbá a befogó fölé rajzolt félkörök területe az S1 hold és az M1 szegmens, illetve az S2 hold és az M2 szegmens területének az összege, az általánosított Pythagoras tétel értelmében igazak a következő egyenlőségek :
Háromszög területe + S1+S2 = (M1+S1) + (M2+S2)
Háromszög területe + S1+S2 = M1+M2 + S1+S2
Háromszög területe = (M1+M2)+(S1+S2)—(S1+S2)
Háromszög területe = M1+M2.
Meglepetéssel látjuk, hogy elemi geometriai eszközökkel sikerült a «holdacskák» területének összegét meghatározni. A háromszög területe ugyanis oldalaiból mindenkor meghatározható. A holdacskák viszont minden oldalról görbe vonallal határolt idomok lévén, joggal kelthették azt a gyanút, hogy területük csak irracionális számmal fejezhető ki. Kétségtelen azonban, hogy ez nem igaz.
Mint említettük, ilyen és hasonló dolgokat már az ókorban is ismertek s ezért azt hitték, hogy a körmérést módszereik tökéletlensége hiúsítja meg. Ehhez járult még egy körülmény. A kvadraturának a térbeli megfelelője az úgynevezett kubatura, vagyis valamely testnek egységkockákkal történő ábrázolása. Már eleve lehetetlen volna egy kilogramm körte lemérése vagy egy-két liter űrtartalma öblös korsó gyártása, ha görbe vonalú, illetve felületű idomok kubaturája nem volna lehetséges. Kubatura és kvadratura lehetősége tehát nem a felületek szabálytalanságán és hajlásán múlik, hanem azon, hogy hiányzik a felület leírásához szükséges matematikai módszer. Derékszögű négyszög, háromszög, gúla, hasáb, vagy akár trapéz és oktaéder területe, illetve köbtartalma meghatározható, ha kellő számú meghatározó adat rendelkezésre áll. Kúpnál, hengernél és gömbnél már a π nem kerülhető el, használata következtében ismét találkozunk az irracionalitás fogalmával. A forgási ellipszoidnál mondjuk, szintén. De a matematika legnagyobb rejtélyei és legégetőbb problémái közé tartozott, hogy miként lehet bonyolult módon görbe felületű vagy körvonalú idomok kubaturáját és kvadraturáját elvégezni, annál is inkább, egyik-másik idom területét illetve köbtartalmát súlymérés alapján meg tudták határozni. Tulajdonképpen már elmondott dolgokat ismétlünk, ha elmondjuk, hogy képzeljük magunkat azon matematikus helyzetébe, akitől megkérdezik : kubaturának tekintendő-e az, ha 25 köbcentiméter, pontosan kimért 1 cm3 nagyságú kockákban előttünk fekvő ólmot beolvasztunk és feltételezve azt, hogy az ólomból nem vész el semmi, valamilyen szabálytalan alakú «kalácsot» öntünk belőle. Mi történik, ha a kalács súlyát lemérve meggyőződünk arról, hogy súlya a 25 kockáéval azonos ; és mégis azt állítják, hogy a kalács kubaturája nem végezhető el? Hisz kiderül, hogy a köbtartalom pontosan 25 cm3. A matematikus nem számára marad más felelet, be kell vallania, hogy a matematika nem tudja a kubaturát elvégezni. Hacsak kerülő úton nem. Például úgy, ahogy Archimedes tette, aki syracusai Hieron király koronájának aranytartalmát azzal határozta meg, hogy a koronát vízbe mártva megmérte és meghatározta a kiszorított víz súlyát. Ez a híres archimedesi tantétel.
De ne szaporítsuk a szót. Évezredek gondolkodása, a legrégebbi időktől Keplerig mégis némi fényt derített a problémára. Úgyannyira, hogy Kepler, aki a nagyon bő bortermésű 1624. évben alapos tanulmányok tárgyává tette a boroshordókat, már nem csak űrtartalmukat vizsgálta, hanem azt is, hogy miként lehet lehető legnagyobb űrtartalmú hordót legkevesebb fából előállítani. (Ennek a követelésnek geometriai jelentése lehető legkisebb felületű idom keresése.)
A tizenhetedik században, — elég ha Fermat, Cavalieri, Pascal, Gregorius a Sto. Vincentio, Wallis, Sluse és de Witt nevét említjük — már minden oldaltól közelebb férkőztek a kvadratura és kubatura nehéz problémájához és sok fontos és helyes összefüggést találtak meg. Részben Archimedes módszerét használták fel, de ezzel itt még nem foglalkozhatunk. Teljes világosságot a dologra csak a Leibniz és Newton által felfedezett infinitézimálszámítás vetett.Ezzel most befejezzük történelmi előadásunkat és megpróbáljuk, a kvadratura problémáját lépésről-lépésre, lehetőleg kézzelfoghatóan megoldani, A probléma kényes, még ma sem teljesen tisztázott filozófiai részeire természetesen nem terjeszkedhetünk ki, nincs is szándékunkban. Oly módon foglalkozunk a problémával, hogy ellenfelünk sokszor fogja kétségbeesetten az égfelé fordítani szemét. De hisszük, hogy többet ér, ha a dolgokat legalább körülbelül értjük, mint ha sehogyan sem. Annál is inkább, hisz nem követünk el mást, minthogy olyan dolgokat írunk le, amelyeket a XVIII. században még a legnagyobb matematikusok sem tartottak helytelennek. S a többre, helyesebbre vágyó olvasó később a matematika nagy és szigorú tudósainak művei segítségével túljuthat a mi kuruzslásszerű tanításainkon.
Bevezetésül megemlítjük, hogy a kvadratura probléma csak akkor lett hozzáférhető, amikor a koordinátageometria ismertté vált. Lényegében csak Descartes után. S most fejünkbe vesszük, hogy olyan idom területét fogjuk meghatározni, amelyet nem csak egyenes vonalak határolnak. Például az OBC idomét.

44. ábra.
A K görbe nem körív. Valamilyen görbe ez, de kitűnik azzal, hogy véletlenül ismerjük az "egyenletét". Legyen ez az egyenlet y=f(x), vagyis bármely x-hez tartozó y behelyettesítéssel kiszámítható. Szándékosan nem írunk ide valamilyen bonyolultabb függvényt, hogy később könnyebben számolhassunk. Feltételezzük azonban, hogy az f(x) valamilyen bonyolultabb kifejezést jelent, olyant, amely együtthatós x hatványokból és állandókból áll. Ilyen kifejezést jelent tehát az f(x), de a részletek pillanatnyilag nem érdekelnek.
A kezdőt ez a megnövekedett általánosság esetleg zavarja. Most már nem is általános számokkal számolunk, hanem még magasabb egységekkel, függvényekkel. Éppen ezért még egyszer röviden rámutatunk a dolgok lényegére.
y=f(x) legyen például

Természetesen éppen úgy lehetne y=3x2+4x+9, vagy valami egészen más is. Például

Valamennyi esetnek közös tulajdonsága az y=f(x) alak. Vagyis mindegyiknél feltételezzük, hogy az x értéke szabadon választható és ezáltal az y értéke is szükségképpen adott. Aritmetikai szempontból tehát mindegy, hogy y-t vagy f(x)-et mondunk. A két mennyiség azonos, geometriai jelentésük ordináta, s az ordináták végpontjai alkotják a görbét.
Még egy kis közbevetett megjegyzés mielőtt még a kvadratura feldezésének nekifognánk. Függvénynek azt a körülményt nevezzük tulajdonképpen, hogy egy mennyiség valamilyen törvényszerűség következtében függ egy másiktól. Minden gyermek tudja, hogy a testek a hő hatására kitágulnak. Ezen a tapasztalaton alapul a higanyos hőmérő is. Tehát mondhatom, hogy a tágulás a hőmérséklet függvénye. Ezrével lehet ilyen példát említeni. Utazásnál a megtett távolság a sebesség függvénye. A szabadesés sebessége függvénye a föld vonzóerejének, az ember testmagassága korának függvénye. Még a bornak, vagy a gorgonzola sajtnak a jósága is függvénye az időnek.
Minthogy a kör területe a sugarától függ, tehát a terület a sugárnak a függvénye. Vegyünk most egy példát a mindennapi életből. Minden dohányos tudja, hogy a vastagabb cigaretta íze enyhébb. Ugyanaz a dohány vékonyabb hüvelybe töltve erősebb ízű, mint vastagabb hüvelyben. Mi ennek a. magyarázata? A magyarázat nagyon egyszerű. A papír mennyisége a cigaretta vastagságával lineárisan növekszik. A kerület=2rπ. Ha r mondjuk 5 milliméter, akkor (2*5*3,14) = 31,4 milliméter papír füstje jut egy szippantásba. Ha r=10 milliméter, akkor a papír égő kerülete (2*10*3,14)=62,8 milliméter. Az égő dohányfelület viszont az r2π képlet adja. r=5 mm esetén a felület (25*3,14)=78,5 mm2, r=10 mm esetén pedig (100*3,14)=314,1 mm2. Egy négyzetmilliméter égő dohányra eső papír vékony cigarettánál sokkal több, mint a vastagnál, vagyis gyakorlatban ez azt jelenti, hogy az "enyheség" négyzetes függvény lévén sokkal gyorsabban nő, mint a lineáris "erősség". Ha függvények képét megrajzolom, ugyanezt látom. (Az «enyheség» képe parabola, az «erősségé» egyenes.) Ezért enyhébb ízű az ugyanolyan anyagból készült vastagabb cigaretta, mint a vékonyabb.
Végül még egy paradoxonnak látszó példa Georg Scheffer könyvéből. Gondoljuk, hogy az egyenlítőn egy csupa 1 méter hosszú részből álló vasgyűrű fekszik. A földet sima, geometriai szempontból is pontos gömbnek tekintjük. Mennyit tágul a gyűrű, mennyire emelkedik fel a föld felszínéről, ha valahol még egy 1 méter hosszú darabot beiktatok. A "józan esze" alapján mindenki azt mondaná, hogy a lazulást bizonyára észre sem lehetne venni. A távolság nem lehet látható, hisz mérete legfeljebb néhány milliomod milliméter lehet. Semmi esetre sem ilyen egyszerű a dolog. Példánk nem csak a «józan ész» megbízhatatlanságáról győz meg, hanem a matematika csodálatos egyöntetűségéről is.
Így következtetünk: az eredeti kör kerülete 2rπ. Sugara tehát



Méterben számolunk, tehát 1 : 2π=1 m : 6,283=15,92 centiméter, kereken tehát 16 centiméter az eredmény. Valóben meglepő! A föld körül fekvő gyűrű 40,000 kilométerébe iktatott egyetlen méter az egészet 16 centiméter magasra emeli. A matematikus nem csodálkozik, ő ugyanis a

összefüggésből látja, hogy a T távolság csak a π-től függ, tehát olyan mennyiségtől, amelynek semmi köze a sugárhoz. Felírná, hogy
y=T=f(π)
s ezzel azt fejezné ki, hogy az eltávolodás új darab beiktatása esetén mindig ugyanannyi, akár az egyenlítőről, akár egy arany karikagyűrűről, vagy pedig a körnek képzelt Neptun-pályáról van is szó. Általános érvényű összefüggés, hogy
y= T = D/2π
ha D jelenti a beiktatott új darabot. Ha történetesen a kör kerületével egyenlő hosszúságú részt iktatok be, vagyis 2rπ-t, akkor az eredmény
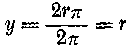
s ez azt mondja, hogy kétszeres kerületű kör sugara is kétszeres. De ezt már láttuk a cigarettával kapcsolatos példán, gaz, hogy fordított felállításban.
A «józan ész» hívei számára csak még azt akarom megjegyezni, hogy 16 centiméter a föld sugarához képest éppen olyan kevés, mint az 1 méter a föld kerületéhez képest. Ha ezt kellőképpen megértettük, felírhatjuk, hogy
16 cm : föld sugara=l m : föld kerülete
s ebbe már belenyugodhatunk.
De most, hogy már megint valamivel műveltebbek lettünk, vissza kell térnünk a kvadraturához.
A feladatunkat már ismerjük : ki kell számítanunk, az y=f(x) görbe, az abszcissza tengely és két ordináta, y1 és y9által határolt területet. (45. ábra.)
A képből kiderül, hogy a keresett terület a függőleges sávok területének kétféle összege közé esik. Az egyik összegbe beleszámítanak a kis, vonalkázott négyszögek is, a másikba nem. Ha nem görbéről, hanem egyenesről volna szó, egyszerű volna a helyzetem.

45. ábra.
Egyenes ugyanis a vonalkázott négyszögeket felezné és ezzel nagyon könnyűvé válnék a helyzetünk. De mivel éppen görbét választottunk számításaink alapjául, tovább kell számolnunk. Mekkora először is az úgynevezett "a görbébe beírt" sávok területe. A sávokat megszámoztuk.
I. sáv = (x2—x1) * y1
II. sáv = (x3—x2) * y2
III. sáv = (x4—x3) * y3
és így tovább, végül
VIII. sáv = (x9—x8) * y8
De minthogy (x2—x1) = (x3—x2)=(x4—x3) stb., minthogy az x értékét mindig ugyanannyival növeltük, jelöljük fenti különbségeket Δx-szel. Ezzel a jelöléssel a beírt sávok területének összege
Sb = y1Δx+y2Δx+y3Δx+y4Δx+y5Δx+y6Δx+y7Δx+y8Δx.
A körülírt sávok magassága természetesen mindenkor nagyobb, mint a megfelelő beírt sávoké. Összegük az ábra értelmében a következő.
Sk = y2Δx+y3Δx+y4Δx+y5Δx+y6Δx+y7Δx+y8Δx+y9Δx.
Emlékezzünk vissza, ilyen összegeket a szumma jellel is írhatjuk. Így az első összeg

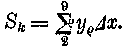


s ez nem egyéb, mint annak a ténynek matematikai fogalmazása, hogy a görbével határolt terület a beírt sávok és a körülírt sávok területének összege közé esik.
Vehetnénk magunknak a fáradságot, hogy az ismert y=f(x) egyenletből az x-ekhez tartozó y értékeket kiszámítsuk. Ezzel megkapnánk úgy a körülírt, mint a beírt sávok területének összegét és tudnánk, hogy a görbe területe valahol a két érték közt fekszik. Ha a, Δx-et mind kisebbnek és kisebbnek választom, akkor ezzel a körülírt és beírt sávok területének különbsége szintén fogy, amint ez a 45. ábra, de még inkább egy külön rajz megfigyeléséből kiderül. Ha ezt az eljárást, amely a valóságot mindinkább kimeríti (innen a neve is exhaustiós módszer, exhaurire=kimeríteni alapján) folytatjuk, hamarosan elég jó közelítő eredményt kaphatunk. Igaz, a munka rendkívül nagy, s mint említettük, az eredmény mégis csak megközelítő. Képzeljük el, hogy ezzel a módszerrel kellene az

Tekintve, hogy x=5 és x=10 közé 999 sávot kell elhelyeznem,

Most egymás után ezerszer kell az y értékét meghatározni.

és így tovább.
Ekkor kellene valamennyi beírt és körülírt sáv területét kiszámítani.
Beírt sávok:

és így tovább.
Körülírt sávok:

és így tovább
Igaz, 999 sáv helyett 1000 sávot is vehettem volna a számítás egyszerűsítésére, igaz továbbá, hogy minden körülírt sáv ugyanakkora, mint a megelőző beírt sáv, mégis látjuk, hogy még egy nagyon egyszerű
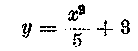
függvény is igen jelentős nehézségeket okoz, s az eredmény mégis csak közelítő.
Más is látszik. Az, hogy az eredmény pontossága a sávok növekvő számával nő. Ha tehát a Δx-et a lehető legkisebbnek választjuk, ha a Δx-ből elenyésző dx-et csinálunk, s ezt választjuk sávjaink alapjának, akkor pontos kvadraturához jutunk. De ehhez végtelen sok y értékét kell kiszámítanunk, mivel minden véges távolság végtelen sok dx-ből áll. Olyan műveletet keresünk tehát a kvadraturához, amely lehetővé teszi, hogy valamennyi, az x1-től xn-ig terjedő tartományon belül fekvő y ordinátát dx-szel megszorozzuk és a szorzatokat összegezzük. A nagy Cavalieri tehát a kvadratura problémáját «Summa omnium y» (valamennyi y összege) alakjában írta. S Leibniz írta egy történelmi nevezetességű papírlapra 1676 október 29-én a következő szavakat: "Hasznosabb lesz ezentúl Cavalieri «summa omnium y» kifejezése helyett az ∫ ydx jelölést írni..."
Ezzel tulajdonképpen elérkeztünk könyvünk tetőpontjához. Leibniz azt állítja, hogy hasznosabb a «summa omnium y» parancs helyett az ∫ ydx integrálparancsot használni. (Az integrál szót Bernouilli alkotta és alkalmazta Leibniz-cel egyetértésben az új, ∫ ydx algoritmus jelölésére.) Nem puszta játék ez a szavakkal? Vagy ismét új "igaz kabbala" rejlik mögötte?
Ezt most lépésről-lépésre kell megvizsgálnunk. Azt legalább már tudjuk, hogy mit kívánnak tőlünk. De lássuk azt még világosabban. Miként a szumma jelnél tettük, az integrál jelére is odaírjuk a határokat, s ezzel «határozott» integrállá alakítjuk. Tegyük fel, hogy az első minket érdeklő x=a, az utolsó pedig x=b. Ekkor ezt írjuk :
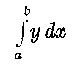
s így olvassuk : "integrál a-tól b-ig ydx."
Még egy lépést teszünk előre. Tudjak, hogy y=f(x), tehát ezt is írhatjuk
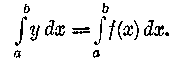
Ezzel a parancs készen áll. Csak még a végrehajtás módszere hiányzik. Mert önmagában véve ismét őrültség, amit a parancs kíván. Nézzük meg csak közelebbről, hogy milyen beteges kívánságot kellene teljesítenünk. Varázsszerkezetünknek nem kevesebbet kellene teljesítenie, mint a következő végtelen sok tagot összegezni:
Első sáv = f(a) dx
Második sáv = f(a+dx) dx
Harmadik sáv = f(a+2dx) dx
Negyedik sáv = f(a+3dx) dx
és így tovább, végtelen sokszor.
«Utolsóelőtti» sáv = f(b—dx) dx
«Utolsó» sáv = f(b) dx.
Itt f(a), f(a+dx) stb. a mindenkori y értéket jelenti, azt, amely az x=a, x=(a+dx), x=(a+2dx) helyettesítésekből adódik. Ezen felül dx határértéke 0 kell, hogy legyen. Amit pontatlanul úgy is mondhatunk, hogy dx végtelen kicsi.
Mivel azonban sem Leibniz, sem a többi nagy tudós, aki ezt a tudományt megalapozta, nem volt őrült, ne okoskodjunk tovább, hanem fogadjuk inkább hálásan kezükből ezt a csodálatos tudományt.
HUSZONÖTÖDIK FEJEZET.
A differenciál és az ívhosszúság mérése.
Már ismételten beszéltünk Δx-ről és Δy-ról, dx-ről és dy-ról. Különösen a dx és dy látszott mintegy a felsőbb matematika kulcsának. Most tehát közelebbről is szemügyre vesszük ezeket az apró dolgokat. Már eleve meg kell jegyeznünk, hogy maga a «dolog» kifejezés is hibás. Mert hiszen valóságban ezek a még véges nagyságú Δx-nek és a Δy-nak eltűnő, vagy már el is tűnt határértékei.
Történelmi és pedagógiai okai vannak, hogy miért nevezzük őket dolgoknak. Ebben a könyvben csak bevezetést adunk, szinte csak felkeltjük az érdeklődést az infinitézimál számítás iránt, tehát ragaszkodnunk kell a szemlélethez. Tudományunk is a szemlélhetőből, a megfoghatóból ered. És így születtek az első nagy felfedezések. Hogy azután további két évszázad logikailag erősen kifínomította, nem jogosít fel arra, hogy az úttörőket lenézzük. A legpompásabb gyémánt is gyakran üvegtörmeléknek látszik, amikor Afrika kék agyagjából napfényre kerül. Nem szabad semmibe sem venni az amsterdami gyémántköszörűs munkáját, hisz ő adja meg a kőnek csillogását és fényét. De gyémánt híján nincs mit csiszolni. És éppen így a differenciál első durva fogalma nélkül nincsen modern, puritán matematika sem.
A finom kérdéseket tehát arra az időre halasztjuk, amikor már későbbi tanulmányok során valamennyi alapismeretét megszereztük. Akkor már örömmel fogjuk egy Cezáro, egy Kowalewski, egy Peano precizitását élvezni és csodálni.
De most vegyünk egy olyan görbét, ahol az x növekedtével az y is nő. Az x növekménye Δx, y-é Δy.
Az x, amely a hozzátartozó y útján egyértelműen meghatározza a görbe szóbanforgó P pontját, Δx-szel, tehát egy véges értékkel nőtt.

46. ábra.
Így keletkezett a hozzátartozó, megnövekedett y érték, y+Δy. Az új ordináta végpontja a P1 pont. PP1 a görbének ívdarabja. Ha nem Δx-szel mennék előre az abszcissza-tengelyen, hanem csak egy majdnem végtelen kicsi dx darabbal, a görbe akkor is emelkedett volna. Igaz, hogy csak egy szintén nagyon kicsi dy darabbal. A P és a P1 pont "kettős ponttá" olvadna össze és a PP1 ívdarab is elenyészően kicsi volna: olyan kicsi, hogy közömbös, hogy görbének vagy egyenesnek tekintjük-e. De éppen ez a körülmény, hogy «közömbös», hogy egyenes vagy görbe, döntő gondolat az infinitézimál számításban.

47. ábra.
Ez teszi lehetővé, hogy egyenes vonalakkal határolt idomokra vonatkozó szabályokat görbe vonalú idomokra alkalmazzunk. Hasznát vesszük a kvadraturánál és a rektifikációnál (magyarázat később) is. De lássuk Leibniz úgynevezett "karakterisztikus háromszögét", hogy mélyebben hatolhassunk be a vizsgálatba. Leibniz Blaise Pascal hátrahagyott feljegyzései közt rajzot talált, amely a sinus-függvény vizsgálatára vonatkozott. Ez a rajz vezette rá Leibnizet nagy felfedezésére, a differenciálszámításra. De zavarok elkerülésére rajzoljuk fel a karakterisztikus háromszöget, anélkül, hogy lényegén változtatnánk, Leibniz rajzától kissé eltérő módon. (47. ábra.)
Tetszőleges görbe A pontjában húzzunk érintőt. Ezen vegyük fel A-tól jobbra is, balra is, ugyanakkora távolságra a B és C pontot. Az A-ból bocsássunk merőlegest az x tengelyre és ugyancsak az A-ban állítsunk merőlegest az érintőre is. Egyszerű geometriai tételekből következik, hogy a vonalkázott háromszög és a vastagon rajzolt háromszög hasonlók. A vastagon rajzolt háromszög átfogója merőleges a vonalkázott háromszög átfogójára s a hosszabbik befogók is merőlegesek egymásra. (így rajzoltuk!) Ebből következik, hogy az előbbinek A-nál fekvő szöge egyenlő utóbbinak B-nél fekvő szögével. De ha két derékszögű háromszög egyik hegyesszöge egyenlő, akkor a másik is az. Azok a háromszögek pedig, amelyeknek megfelelő szögeik egyenlők, hasonló háromszögek.
Gondoljuk mármost, hogy B és C egyenletesen közelednek A-hoz. Ezzel a vonalkázott háromszög mind kisebb és kisebb lesz, anélkül, hogy alakja változnék. Végül már elképzelhetjük, hogy a B és a C A-ban szinte összeütköznek. Ezzel már kezünkben van a differenciál csodája: az A pontban van most egy szinte mikroszkópikusan kicsi, szabad szemmel láthatatlan háromszög. De alakját a hozzá képest óriási vastagon bekeretezett háromszög megőrizte. És ezzel a szögeit is, valamint oldalainak a viszonyát. De még egy csoda történt. A vonalkázott háromszög átfogója az A pontban rajzolt érintőnek egy része. Tehát az A pontban, amely az érintőhöz és a görbéhez egyaránt tartozik, egy apró egyenes érintődarabka rejlik, de az ugyanakkor a görbe apró ívdarabjának is tekinthető.
Belátjuk, hogy felváltva görbe, majd egyenes ívelem Janus-fejűsége a «fekete mágiám emlékeztet. Gondoljunk azonban a kerékpárláncra, amely egyenes darabokból áll és mégis odasimul a fogaskerekekhez. S képzeljük el, hogy a láncszemek végtelen kicsinyek. Természetesen logikánk azt mondja, hogy van egy pont, ahol valami megszűnik egyenes lenni. Egyenes és görbe bizonyos álláspontból tekintve olyan különbözők, mint tűz és víz, mint fekete és fehér. Viszont más oldalról nagyon is könnyen elképzelhető az átmenet. Valamely kisebb tó felszíne ideálisan síknak látszik, bár a föld gömbalakja miatt jól lemérhetően görbe. De kevésbbé görbült, ha ugyanazt a tavat a Nappal egyenlő nagyságú gömb felületén gondolom. Tejút méretű gömbön görbültsége még kisebb. A differenciálra vonatkozó elképzelésünk éppen ilyen méreteket tüntet fel. Mert végre is, elképzelhető, hogy a B és a C pont mind közelebb kerül egymáshoz.
Ideális esetben az A pontunk egy nagyon kicsi vonalkázott háromszöget tartalmaz. Ez mindenkor hasonló a karakterisztikus háromszöghöz, tehát óriásira nagyítva le tudjuk rajzolni.

48. ábra.
Három oldalát differenciáloknak nevezik. Az abszcisszatengellyel párhuzamos befogó a dx, a másik dy és az átfogóként mutatkozó, Janus-fejű «ívelemnek», jele ds.
De a görbe bármelyik pontját tekinthettük volna egy karakterisztikus háromszög csúcsának. S ha eljárásunkat a görbe minden pontján megismételjük, akkor görbénk ilyen vonalkázott háromszögek gyöngysorának fogható fel. Az ívhossz tehát az ilyen ds ívelemek összege. Óriási nagyítással ilyen volna a görbénk :

49. ábra.
De teljesen félreértjük az analízis célját, ha túlságosan ragaszkodunk a karakterisztikus háromszöghöz fűződő elképzelésünkhöz és megfeledkezünk a legelső rajzunkról. Figyelembe kell vennünk, hogy a dx1, a dx2 stb. az x-nek apró növekményei, a dy1 stb. pedig az ezekhez az y=f(x) összefüggés következtében tartozó növekmények. A ds1, ds2 az e közben keletkező ívelemeket, érintő elemeket jelenti. A görbéket ugyanis számtalan érintőelemből is származtathatjuk. Ha például itatóshenger billeg a papíron, akkor a papír jelenti az érintőt és az itatós a görbét. Ha az egészet megfordítom és a hanyatt fektetett itatóshengeren merev vonalzót gördítenék végig, akkor a vonalzó az érintő és a görbét végtelen nagyszámú érintőelemből származónak tekinthetnek. A geometriában gyakran szoktak görbéket érintőik segítségével megrajzolni. Szigorúan véve a körző hegye sem más, mint a kör érintőjének kis része.
50. ábra.
Eddigi tanulmányaink nagy, összefoglaló ismeretek küszöbére vezettek. Ezek az ismeretek egy csapásra megadják az egész felsőbb matematika algoritmusát.

Először lássuk a rektifikációt. Így az ívhossz nagyságának megállapítását nevezik. Tekintve, hogy hosszúságmérőnk egyenes darabokból áll, gondolatban a görbét ki kell egyenesítenünk («rectam faeere»). Innen a rektifikáció elnevezés. Elvben ez nem nehéz. Valaha azt hitték, hogy görbe ívhosszát csak irracionális szám fejezheti ki. Akárcsak a racionális sugarú kör kerületét. Már utaltunk arra, hogy az irracionális relatív fogalom. Görbéknek általában nem kell, hogy közük legyen hozzá. Bármilyen hosszúságú zsinórt tudok görbeként az asztalra fektetni. Mindez mellékes. Tudjuk, — vissza kell már térnünk végre a rektifikációhoz — hogy minden görbe a ds-ek gyöngysora. De mindegyik ds kifejezhető Pythagoras tételével: (ds)2 = (dx)2 + (dy)2 vagy

Az a∫b ds integrált még csak megoldanánk egyszerű megfontolások alapján. Az a és b abszcisszák közti ívhosszat jelenti. De ezzel még semmire sem mentünk. Mert ez nem a felelet, ez a kérdés. Felelet csak a
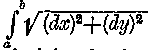
Ezzel visszatértünk kiindulópontunkhoz. Tudjuk már, hogy mit kellene tennünk a kvadraturánál és a rektifikációnál. Sőt ehhez már szép varázsjelünk is van. De mintha gyökeret vert volna lábunk, nem tudjuk az integrál-parancsot végrehajtani, hasonlóan ahhoz az alvóhoz, aki álmában nem tud megmozdulni, míg végre gyötrelmében megizzadva felébred. Ezt a megmentő felébredést legközelebbi fejezetünk hozza számunkra.
HUSZONHATODIK FEJEZET
A differenciálhányados és az integrál összefüggése
Már láttuk, hogy tisztán aritmetikai módon meg tudjuk határozni, nem ugyan magukat a differenciálokat, hanem a viszonyukat, a differenciálhányadost. Vagyis dy/dx értékét, ha ismerjük az y=f(x) függvényt. Két függvény deriváltját, a differenciálhányadost így is nevezik, meg is határoztuk. És elhiheti az olvasó, hogy bármely függvény egyszerűbb vagy bonyolultabb számítással differenciálható. (Természetesen feltéve, hogy nincsenek a függvénynek a differenciálhatósággal ellenkező tulajdonságai.) Nemsokára megismerkedünk a differenciálás szabályaival és látni fogjuk, hogy az éppen olyan biztosan kezelhető művelet, mint pl. a szorzás. Megoszlanak a vélemények arról, hogy a tetikus vagy pedig a litikus műveletek csoportjába tartozik-e. Mert tulajdonságai mindkét típusra emlékeztetnek. De ezen egyelőre ne törjük tovább fejünket, inkább lássuk, nem adja-e kezünkre a differenciálhányados az integrálszámítás kulcsát. Aritmetikai eszközökkel fogunk munkához, egyelőre mellőzzük a geometriát. Hisz már az imaginárius számok tanulmányozásakor sikerült egy hozzáférhetetlennek látszó rejtélyt megoldani s kimutatni, hogy az i a 90 fokhoz tartozó forgási tényező.
A kvadratura-feladat Terület = ∫ ydx és Terület = ∫ f(x) dx alakú parancsokra vezetett. Mindkét parancs tartalmazza a görbe egyenletét (egyszer az y ordináta alakjában, másodszor az azzal egyenlő f(x)-ként), valamint a dx-et. Először azt a kérdést kell vizsgálnunk, hogy vajon ez a dx az f(x)-ből származik-e. Határozottan látjuk, hogy nem. Mert csak ezt az egyenletet ismerjük

Eddigi ismereteink szerint dx sohasem tartozik «törzs-függvényhez», hanem mindenkor a törzsfüggyény y' vagy f'(x) alakban írt deriváltjának, differenciálhányadosának része. Most gondolatban azt a merész fogást alkalmazzuk, amelyet Leibniz használt a történelmi jelentőségű 1676 október 29. napon. Az integrál jel mögött álló kifejezést nem törzsfüggvénynek, hanem differenciálhányadosnak fogjuk tekinteni. Ismét hangsúlyozzuk, valójában ezzel semmi sem változott. Csupán felfogásunk kabbalájában történt változás. Ha annak a görbének, amelynek a területét meg akarjuk határozni, y=x2 volt az egyenlete, akkor az is marad. Csupán azt állítjuk; hogy létezik egy másik olyan F(x) függvény is, amelynek y=x2 a differenciálhányadosa.
Tudjuk, hogy elképzelésünknek ilyen változtatása jelentős nehézsége az infinitézimálszámítás megértésének. De ha megértettük ezt a fogást, akkor minden további könnyű és többé-kevésbbé gépiesen végezhető. De bármilyen nehéz is a dolog, gyerünk tovább. Egyszerűen tegyük fel, hogy előttünk áll a

differenciálhányados.
Aritmetikai szempontból ez éppen olyan egyenlet, mint bármely másik. Vagyis az egyenletekre vonatkozó szabályok szerint bánhatok vele. Tehát megszorozhatom dx-szel. Ne zavarjon e közben, hogy két egyenlőségi jel szerepel. Mert ha egy derékszögű négyszögnek a=5 és b=3 volnának az oldalai, akkor írhatom, hogy T=a*b=5*3, sőt azt is, hogy T=a*b=5*3=15 és minden helyes marad, ha 2-vel szorzók és írom : 2T=2ab=2*5*3=30. Tehát szorzunk dx-szel, az eredmény :

vagy dy=f'(x)dx=y'dx.
De a mérlegnél tanultak szerint az egyenlőség nem változik, ha egyenlő dolgokon azonos műveleteket végzünk. Tehát minden oldalon kiadhatjuk az integrálparancsot:
∫dy = ∫f'(x) dx = ∫y'dx.
Meglepetve látjuk, hogy az integrálnak igen fontos tulajdonságának jöttünk nyomára. Arra, hogy a differenciálásnak megfordított művelete. Mert ha ismét elhagyom az integráljeleket (mostani tudásunk alapján integráltalanításnak neveznénk ezt a műveletet), akkor a
dy = f'(x) dx = y'dx
egyenlőséget, ezt dx-szel osztva a

egyenlőségeket, vagyis végül az eredeti differenciálhányadost kapnám. Már csak azzal kell törődnünk, hogy mit jelent az ∫dy. Jelenti valamennyi, végtelen sok dy-nak, tehát valamennyi y növekményének az összegét, a görbe általunk választott tartományában. Természetesen arról a görbéről beszélünk, amelynek egyenletét differenciálnunk kellett, hogy y'-t, illetve f'(x)-et kapjunk. Tehát az integrálásnál keresett, ismeretlen, törzsfüggvényről van szó. Írhatjuk tehát
f(x) = y = ∫y'dx = ∫ f'(x) dx.
Ezzel megadtuk az integrálszámítás feladatát. A feladat a következő : ha egy megadott függvényt integrálunk, eredményül a törzsfüggvényét kapjuk, azt a függvényt, amelynek differenciálhányadosa a megadott függvény.
Kezdőnek itten nehézséget okozhat a szokásos jelölési mód. Ha ugyanis a megadott függvényt y=f(x)-szel jelöltük, akkor a törzsfüggvényt, megkülönböztetésül F(x)-szel kell jelölnünk és y helyett is más betűt, mondjuk Y-t kell használnunk. Fenti egyenlőség ez esetben így fest:
Y= F(x) = ∫f(x) dx = ∫y dx.
Ha viszont a megadott függvény jelölésére már az y'=f'(x) jelölést használtuk, akkor a törzsfüggvényt jelölhetjük y=f(x)-szel. Ez esetben az egyenlőség a következő :
y = f(x) = ∫f'(x) dx = ∫ y'dx.
Fel kell itt egy kézenfekvő kérdést is vetnünk. Miért írtuk a quadratura és rektifikáció feladat megoldásához az integrál jele mellé a határokat s miért hagytuk el őket most? Nem egyszerű a felelet. Létezik ugyanis "határozott" és "határozatlan" integrál. A határozott integrál körülhatárolt tartományon belül végzett összegezés eredményét adja, a határozatlan viszont nem határolt tartományban végzett összegezés eredményét. Nagyjából azt mondhatnánk, hogy ugyanaz a viszony a határozott integrál és a határozatlan között, mint a konkrét szám és az általános közt. Ha a határozatlan integrált ismerem, amelyet "általános" integrálnak is hívnak, akkor határok behelyezésével mindenkor «határozott» integrálhoz juthatok. De mindezt hamarosan gyakorlatból is meg fogjuk ismerni.
Most azonban a differenciálszámítással kell foglalkoznunk, hogy meg legyen a lehetőségünk az integrálok kiszámítására. E közben a szokásos eljárással ellentétben a két műveletet mindenkor együtt fogjuk tanulmányozni. Előkészületként azonban még két kis dombon kell keresztüljutnunk. Foglalkoznunk kell a különböző rendű kicsinyek analízisével és meg kell ismernünk az úgynevezett binomiális tételt, amelynek általánosabb érvényű alakját Isaac Newton vezette le.
HUSZONHETEDIK FEJEZET
A háromféle semmi
Mit jelent az, hogy különböző rendű kicsi? Már utaltunk rá, amikor az infinitézimálszámítással kapcsolatban «kicsiny»-ről "még kisebb"-ről és "legkisebb"-ről beszéltünk. Azt állítottuk, sőt törteken be is mutattuk, hogy a (dx)2 mindenkor elhanyagolható a dx mellett, mivel az x úgy aránylik a dx-hez, mint a világmindenség a Földgolyóhoz, a dx pedig a (dx)2-hez, mint a Földgolyó a porszemhez. Ha most valamilyen rajzon a Földet tekintem az ábrázolható legkisebb pontnak, akkor a porszem már szóba sem jöhet. Nem szabad ugyan elhallgatnunk, hogy ezt a felfogást nagyon sokan támadják. Elismerik, hogy gyakorlatban nem kell a porszemet tekintetbe venni, sőt elméletben is szabad elhanyagolni, de tulajdonképpen nem lehet tőle megszabadulni. S azt állítják, hogy az infinitézimálszámítás ilyen körülmények közt nem «preciziós» matematika, hanem csak «approximációs» (közelítő) matematika, ugyanúgy, ahogy csak közelítés volna minden számítás, amelyben irracionális szám előfordul.
Érdekes lenne ugyan megismerni azokat a modern kísérleteket, amelyek ezen a nehézségen igyekszenek segíteni, de meg kell maradnunk kereteink közt. Inkább megkíséreljük a különféle rendű kicsit kézzel foghatóan bemutatni, azáltal, hogy rajzban mutatjuk be a háromféle semmit.
Képzeljünk el egy derékszögű parallelepipedont (egy oszlopot, amelynek összefutó élei merőlegesek egymásra). Legyen ez az oszlop fémből s a fém, miként a többi, táguljon a hő hatására. Rögzítsük ezt az oszlopot oly módon, hogy a tágulás csak három lapja irányában történhessék, például azzal, hogy egy szoba sarkában helyezzük el.

61. ábra.
Az oszlop természetesen nem tágul külön a különböző irányokban, hanem egyszerre. Várjuk meg, míg az oszlop eléri legnagyobb térfogatát és bontsuk most részeire. Mégpedig oly módon, mintha a három F1, F2, F3 felület mindegyike a többire való tekintet nélkül növekedett volna, előre illetve felfelé. (52. ábra.)
Könnyebb megértés kedvéért a növekmény egyes részei kétszer láthatók a rajzon: az együttes képen és külön is. Világos, hogy az oszlop, ha ismét eredeti hőmérsékletére hűtjük le, eredeti térfogatára zsugorodik össze.
A növekmények nulla méretűre zsugorodnak, mondanánk az aritmetika nyelvén.
Semmivé lesznek. De közvetlenül mielőtt megsemmisülnének, nagyságuk csodálatosképpen lényegesen különböző. Az oldalak növekményeiből (F1, F2, F3) vékony lapocskák lesznek, a három rúd alakú kitöltőrész (G1, G2, G3) vonalakká, a kockaszerű képződmény (P) ponttá zsugorodik.

52. ábra.
Ismét ama rejtélyes jelenségre bukkanunk, hogy a semminek fokozatai vannak. Felület-semmi, vonal-semmi és pont-semmi nem egy és ugyanaz. Különböző rendű semmik ezek, ha szabad ezt a kifejezést használni. Csak utalunk arra, hogy ezt másképp is kifejthetjük, ha a pontot a semmi «egységének» tekintjük. A pont az egy semmi. A vonaldarab végtelen sok pont sorozata, tehát végtelen sokszor nagyobb mint a pont, mindamellett, hogy szintén semmi. Sőt a felület az hosszúságnak és szélességnek a szorzata, tehát végtelenszer végtelen, tehát végtelen a négyzeten számú pontot tartalmaz. Jóllehet, hogy képzelt határaival és vastagság híján szintén a semminek egyik fajtája.
A valami, fizikai szempontból csak a harmadik dimenzióval kezdődik. «Valami» és három "dimenzió" bizonyos szempontból elválaszthatatlanok. De ne merüljünk túl mélyen a halmazelméletbe, a felső matematikának új és nagyon elvont részébe. Csak azt állapítjuk meg, hogy nemcsak logikai és aritmetikai szempontból, hanem kézzelfoghatóan is meggyőződtünk arról, hogy nem csak nagy méretek közt, hanem a kis méretek világában is van értelme és jelentősége a nagyságrend fogalmának. S beszélhetünk első-, másod-, harmad-stb. rendű kicsiről, dx elsőrendű kicsi, (dx)4 negyedrendű kicsi, (dx)n n-ed rendű kicsi és így tovább a ∞ rendű kicsiig, vagy a többszörösen ∞-ed rendű kicsiig. A józan ész tiltakozik ugyan az ellen, hogy a legkisebb alatt még kisebbet keressen, de ugyanaz a józan ész követeli, hogy valamely önmagával megszorzott kicsi kisebb legyen, mint a szorzatlan.
Ugyanúgy, ahogy 1/10 nagyobb, mint 1/10 * 1/10. Lehetséges volna az az ellenvetés, hogy nem szabad a végesben érvényes és bizonyítható fogalmakat és szabályokat egyszerűen ama ellenőrizhetetlen és elképzelhetetlen műveletekre alkalmazni, amelyekben a végtelen is szerepet játszik. Jó kifogásunk van ez ellen, az, hogy tulajdonképpen nem is végtelen kicsivel, hanem csupán tetszés szerint kicsivel dolgozunk. A nullát csak határértékként alkalmazzuk s nem vele végezzük a műveleteket. Továbbá mindenkor módunkban van verifikálni infinitézimális állításunkat, ha nem is tudjuk esetleg bizonyítani.
De érdekes tárgyalásainkat félbe kell szakítanunk, hogy megint valamilyen konkrét dologhoz foghassunk s utolsó előkészületeinket a csúcs meghódításához megtehessük. Összeszedjük tehát eddigi tudományunkat, hogy megbirkózhassunk a híres "binomiális tétellel". Többféleképpen bizonyítható a tétel. Mi az elegáns kombinatorikai bizonyítást fogjuk követni, hogy tisztán láthassuk a kombinatorika és a már többször említett binomiális együttható összefüggését.
HUSZONNYOLCADIK FEJEZET
Binomiális tétel
Tisztázzuk először a fogalmakat. Binom az (x+a) vagy (x+b) alakú kifejezés, s ha szorzat tényezőjeként jelentkezik, akkor neve binomiális tényező. Az a láttára senki se gondoljon ismeretlenre, jelentősége sokkal inkább az, hogy a két tag már első pillanatra megkülönböztethető legyen. (Az x használatát úgy is lehet magyarázni, hogy a binomiális tétel olyan függvények kifejtésére használatos, amelyekben az x változó szerepel.)
Binom általában az olyan kifejezés neve, amely két szám összeadása vagy kivonása útján keletkezett és valamilyen szempontból új egységnek tekintendő.
Ha az (x+a) és (x+b) binomot összeszorzom, vagyis az (x+a) és az (x+b) binomiális tényezők szorzatát képezem, akkor a következő az eredmény:
(x+a)(x+b)=x2+ax+bx+ab = x2+(a+b)x+ab
Hasonlóképpen
(x+a)(a+b)(x+c) = —x3+(a+b+c)x2+(ab+ac+bc)x+abc
Erről minden olvasó könnyen meggyőződhet.
Abból a célból, hogy az eredmény szerkezete világosabban lássuk, írjuk eredményünket úgy, ahogyan azt már Leibniz is írta néhány alkalommal.

Gyakorlott szem két dolgot már itt is észrevesz. Előbb azt, hogy a valamennyi binomiális tényezőben szereplő a az eredményben fogyó hatványai szerint rendezve jelentkezik. Másodszor azt, hogy az a hatványok együtthatóinak kétségtelen a kombinatorikus jellege, hisz elől az a, b és c elemeknek első osztályú kombinációit látjuk, utána a másodosztályúakat, végül pedig a harmadosztályúakat. Az elemek ismétlés nélküli kombinációkban jelentkeznek. Erre a célra valamennyi, a binomokat alkotó, nem egyenlő a, b, c tag rendelkezésre áll.
Könnyebb és jobb áttekintésül lássunk még egy, valamivel bonyolultabb példát.
(x+a)(x+b)(x+c)(x+d)(x+e)=

E különös struktúra keletkezésének az oka nem is olyan talányos, mint amilyennek első pillanatban látszik. A szerkezet úgy keletkezik, hogy szorzás közben esetünkben mindenkor öt-öt tényezőt kell összeszorozni. (Általában annyit, ahány binomot összeszorzunk.)
x5 nem egyéb, mint x*x*x*x*x és ax4 annyi mint x*x*x*x*a. Továbbá acex2 ugyanaz, mint a*c*e*x*x. Ennyi utalás egyelőre talán elégséges arra, hogy a gondolkodó olvasót a kombinatorikai összefüggés igazságáról meggyőzze.
Foglaljuk most össze az eddig tanultakat szabállyá és határozzuk meg olyan binomok szorzatának általános alakját, amelyekben az egyik tag x, a másik viszont mindegyikben más és más.
Ilyen binomok szorzata x fogyó hatványai szerint rendezett sornak fog adódni, az első tagban az x kitevője azonos a binomok számával. Ebben a hatványsorban a kitevő tagról-tagra eggyel csökken, x1 után még van egy tag: x0, az eredmény tehát a binomok számánál eggyel több tagot tartalmaz. A sor, egyelőre együtthatók nélkül, a következő:
xn+xn-1+xn-2+ ... x2+x1+x0
n a binomok száma. Írjunk minden egyes taghoz együtthatót:
C0xn+C1xn-1+C2xn-2+ ... Cn-2x2+Cn-1x1+Cnx0
Az együttható indexe megmutatja, hogy az együttható az n elemnek hányadosztályú kombinációit jelenti. xn együtthatója C0=1, tekintve, hogy ez a tag csak x-ből áll. Az xn-1 együtthatója az n elemből képezhető valamennyi első osztályú, az xn-2-é valamennyi másodosztályú, az xn-3-é valamennyi harmadosztályú stb. kombináció. Még pedig ismétlés nélküli kombináció. De ezek a kombinációk már nem csupán különböző csoportosításban felírt elemek, itt már az elemeket össze kell szorozni, tehát kombinációk képzését és szorzást kell egyidőben végezni.
Ismét egy fogáshoz folyamodunk. Az eddig különböző a, b, c stb. tagokat egyenlőknek fogjuk tekinteni, vagyis a=b=c=d=e ezáltal a kérdéses szorzatot egyszerűen így írhatjuk :
(x+a)(x+a)(x+a)(x+a)(x+a) stb.
vagy ami ugyanaz
Most jutottunk a matematikában oly nagy jelentőségű binomiális tétel lényegéhez. A megoldás lehetővé teszi, egyelőre ugyan csak pozitív egészszámokra nézve, hogy valamely binom minden hatványát x fogyó hatványai szerint rendezett hatványsor alakjában közvetlenül felírhassuk. Most már közömbös, hogy továbbra is x-et írok-e, vagy valamilyen más betűt írok helyébe. Mi csak azért használjuk továbbra is az a:-et, hogy az előzőkkel való összefüggés világosan megmaradjon.
Eddigi szabályaink szerint az n-szer tényezőnek vett (x+a) vagyis az (x+a)n kifejtve így írható
C0xn+C1xn-1+C2xn-2+ ... Cn-2x2+Cn-1x1+Cnx0
C0=1, ezt már tudjuk. De mennyi a C0, C2, C3 stb? Gondolkozzunk logikusan. C1 az n darab binom x-től különböző tagjából alkotható valamennyi elsőosztályú kombináció összege. Az összeadandók mindegyike a-val egyenlő, a tagok száma n, vagy kombinatorikai jelöléssel


C2 a másodosztályú kombinációk összege. A kombinációk mindegyike a*a=a2, számuk


A harmadosztályú kombinációk a*a*a=a3 alakúak. C3 ezek szerint
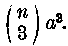

Mielőtt még példát dolgoznánk ki, ismerjük meg előbb a "Pascal-féle háromszög" néven ismert táblázatot. Erről lehet ugyanis legkönnyebben leolvasni a valamely hatványhoz tartotó binomiális együtthatókat. A Pascal-féle háromszög a következő:

és így tovább.
Kissé körülményes volna a bizonyítás, ezért csak felhívjuk arra a figyelmet, hogy a táblázat belsejében bármely szám a fölötte jobbra és balra olvasható két szám összege. Ezzel egészen gépiesen bármeddig tudjuk a táblázatot folytatni.
Említsük még azt is, hogy Pascal az általa felfedezett háromszöget «triangulus mathematicus»-nak nevezte, de a binomiális együtthatókat előtte már Stifel is említi 1544-ben, kínai matematikusok pedig már a Kr. u. XIII. században ismerték.
Joggal kérdezhetjük immár, miként kell ezt a táblázatot használni? Használata nagyon egyszerű. A baloldalon olvasható római számok azt a pozitív, egészszámú hatvány-kitevőt mutatják, amelyre a binomot emelni akarjuk. Az ugyanazon sorban, a háromszögben olvasható számok pedig sorban az előbbi C0, C1, C2 ... Cn-1, Cn értékei. Ezek szerint a számok a kombinatorikai jelölésmóddal írt együtthatóval azonosak. Írjuk fel ezek alapján (x+a)7 értékét x fogyó hatványai szerint rendezett hatványsorban.
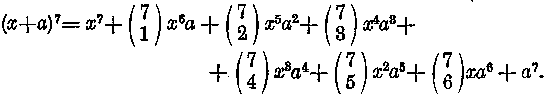
Ha kiegészítésül x7 mellé kiírjuk a

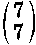

kiszámított értékük: 1 7 21 35 35 21 7 1
s ezzel a Pascal-féle háromszöget hibátlanul verifikáltuk.
Még egy példa.
(4+7)5? Természetesen egyszerűen összeadhatnánk a két számot és közvetlenül felírhatnánk a 11 ötödik hatványát, 115=161051. De felhasználjuk az alkalmat a binomiális tétel újabb kipróbálására és megjegyezzük, hogy a gyakorlati számolás szempontjából is előnyös valamely számot, hatványozásra binommá szétszedni. (Helyértékrendszerben írt számok négyzetre, köbre emelése és általában hatványozása is ezen alapul. Pl. 132=(10+3)2 stb.)
Így számolunk:

s megkaptuk a várt, helyes eredményt.
Második példa.
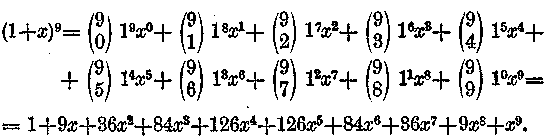
Jegyezzük meg végül, hogy a binom természetesen (x—a) vagy (—x—a) is lehet. Az előjelet a szorzásnál és hatványozásnál tanultak szerint kell az a; és az a előforduló hatványaiból megállapítani. Ha például (x—a)4 kiszámításakor 4x3a előjelét kell megállapítanunk, akkor világos, hogy az előjel mínusz. Mert a szorzat 4*x*x*x*(—a), az eredmény pedig —4x3a.
Írjuk végül a binomiális tételt szumma alakjában,

A matematika azonban a binomoknak nemcsak pozitív egész számú hatványaival foglalkozik. Foglalkoznunk kell tehát azzal az esettel is, amikor a kitevő tört, vagy negatív szám. Először az (1+x)n binommal foglalkozunk és azt kívánjuk, hogy n tört vagy negatív szám legyen.
Kereteink közt nincs módunkban ennek az esetnek is a mélyébe hatolni, tehát meg kell elégednünk annak megállapításával, hogy tört vagy negatív kitevőre binomiális képletünk végtelen «binomiális sorrá)) alakul át. Ennek alakja:

Benne r véges számot jelent, amely n-nél nagyobb is lehet. Ha történetesen nem (1+x) valamilyen hatványát akarom binomiális sorba fejteni, hanem (a+x)+ét, akkor ismét egy fogást kell használnom. (a+x)n egyszerűen


Erre, mint említettük, csak utalunk. De ha már "végtelen sorok" szóba kerültek, röviden meg kell magyaráznunk, hogy mit is nevezünk általában «sor»-nak.
A sor szó maga is mutatja, hogy tagoknak egymás utáni sorozásáról van szó. S a tagokat összeadással vagy kivonással fűzzük egymáshoz. Véges a sor, ha véges számú tag után megszakad, ellenkező esetben végtelen. Végtelen például a
Leibniz-sort:

+5+7+-•• vagy hasonló sorok összege szemmel láthatóan végtelen. Ilyen sort divergensnek, széttartónak mondunk.
A matematika legnehezebb problémái közé tartozik annak megállapítása, hogy valamely sor konvergens-e vagy divergens. Mert szükséges ugyan, hogy a tagok fokozatosan csökkenjenek, közeledjenek nullához, de ebből még nem következik az, hogy a sor konvergens. Így például a végtelen

sor divergens, bár minden tagja kisebb a megelőzőnél. A sor összege végtelen, míg például a szintén végtelen

sor konvergens és összege 1.
Végtelen sorok gyakran tesznek jó szolgálatot kvadraturaproblémák megoldásakor. Az integrálandó függvényt sorrá alakítva megkönnyíthetjük az integrálás elvégzését. Már Archimedes is alkalmazott konvergens végtelen sorokat kvadraturaproblémák megoldására.
HUSZONKILENCEDIK FEJEZET