Törtrendszerek
Fordítsuk figyelmünket a törtrendszerekre, ez sokkal előbbrevaló feladat és különleges esetükre, a tizedestörtekre. A számrendszerekre vonatkozó vizsgálataink nyomán sejthetjük, hogy a «törtrendszer» mit jelenthet. Minden számrendszerben van olyasvalami, ami a tizedestörteknek megfelelője. A hatosrendszerben a «tizedespont» után (ott "hatodospont" lehetne a neve), a hatodok, harminchatodok, kétszáztizenhatodok stb. következnek. A kettesrendszerben a «kettedespontot» a felek, negyedek, nyolcadok, tizenhatodok stb. követik, a tizenhármasrendszerben a tizenharmadospont után a tizenharmadok, százhatvankilencedek, a kétezerszázkilencvenhetedek stb. sorakoznak, a tizesrendszerben a tizedek, századok, ezredek stb. Helyértékrendszerben írt számnak az alakja, rendszerben írt törttel, a következő, ha példaképpen öt egész és négy törtjegyet tartalmazó számot írunk fel és a kitevőket tizesrendszerben írjuk:

vagy egyszerűbben, ha negatív kitevőjű hatványokat alkalmazunk :

A tizedespontot a qg0 és rg-1 közé kellene tennünk. De nem akarunk itt az összes lehetséges rendszerrel foglalkozni, hanem megelégszünk a tizesrendszer vizsgálatával. Tizesrendszerű szám, mondjuk az 50341.7328, amelynek tizedes jegyei is vannak ilyen alakú, lenne: 5*104+0*103+ 3*102+ 4*101+l*10°+7*10-1+3*10-2+2*10-3+8*10-4 s ez a felépítési módját teljesen áttekinthetővé teszi. Tehát még egyszer : rendszerben írt tört alatt törtszámnak számrendszerben írt alakját értjük. Jelölésére rendesen a kis görög σ (szigma) betűt használjuk. De még mielőtt az ilyen rendszertörtek különböző fajtáit megismernénk, ismerkedjünk meg egy új szimbólummal, amely az ilyen rendszeres sorok írását nagymértékben megkönnyíti.
Ez az úgynevezett szumma-operátor, vagy szummajel, «szummája .. .-nek». Jele a görög nagy Σ (szigma). Ki kell még tűznünk az összegezés határait. Ilyen határoknak csak akkor van értelmük, ha csupa lényegében egyforma szerkezetű kifejezés összegéről van szó és ezek csak valamilyen indexben különböznek egymástól. Sejteni kezdjük, hogy sorként írt tizes- vagy másrendszerbeli szám ennek a feltételnek megfelel. Hisz helyértékkel írt szám minden egyes tagja együtthatóból és alapszámból áll, az előbbieket indexük, az utóbbiakat kitevőjük teszi felismerhetővé s az index és a kitevő közt határozott összefüggés áll fenn. A következő, helyiértékrendszerben írt szám: a1g0+a2g1+a3g2+a4g3+a5g4+a6g4+a7g6+a8g7 minden tagja a-ból és g-ből áll. Tehát valamennyi tag a és g szorzata. De melyik a és melyik g veendő tekintetbe? Nos, az 1-től 8-ig terjedő indexű a-k szorozva a 0-tól 7-ig terjedő kitevőkkel ellátott g-kel s minden tagban (ez az összefüggés) az index eggyel nagyobb mint a kitevő, vagy ami ugyanaz, a kitevő eggyel kisebb mint az index. A szám tehát valamennyi avgv-1 vagy alakú kifejezésnek összege. A v (nü) és a ς (ró) görög kisbetűk. De ezzel még nincs a dolog befejezve. Még nem ismerem a határokat, amelyeken belül az összegezést el kell végeznem. Hogyan segíthetek itt magamon? Egyszerű! Mivel az index legkisebb értéke 1 és a legnagyobb 8, így «futásának» alsó határa 1, felső határa pedig 8. A határok mindenkor bezárólag, inkluzive értendők. A hatványkitevőnek viszont alsó határa 0, felső pedig 7. Tehát 0-tól 7-ig «fut». De felhívjuk itt a figyelmet arra — és ez igen fontos, alapvető megjegyzés — hogy ezt a «futást» nem-folytonos, szaggatott futásnak nevezik. Ez tulajdonképpen ugrás egyik egészszámú indexről a másikra, egyik kitevőről a másikra. Vigasztalásul megemlítjük, hogy a rettegett integrál lényegében nem egyéb, mint ilyen sorösszegezés, de ott a «futás» nem szaggatottan, hanem folytonosan történik. Tehát, ha a Σ=összegezési parancsot alaposan emlékezetünkbe véssük, sokat haladtunk az integrál fogalma szempontjából. Mert az összegezést, szumma-parancs lényegében nem egyéb, mint a nem folytonos, eldurvult, szinte szabad szemmel is áttekinthető integráloperátor.
És — ezt már itt eláruljuk — a nagy Leibniz 1676 október 29-én írta fel ama nagyjelentőségűvé vált papírlapra, hogy az új (integrál) jel ∫ nem jelent egyebet, mint összegét valaminek. Ez a jel nem is más, mint eltorzított, széthúzott nagy latin S betű.
De mivel ellenfelem már öklével veri az asztalt és haját tépi, ijedten térek vissza szumma-jelemhez. Azt mondja ugyanis, mikor már kissé magához tért, hogy még azt sem tudjuk, mi a tizedestört.
Megállapítjuk tehát, hogy az ag szorzatoknak mind az indexei, mind a hatványkitevői valamilyen alsó határtól valamilyen felső határig «futnak». Ez annyit tesz, hogy egymás után, mindenkor egészszámot ugorva, felveszik a felső és az alsó határ közötti értékeket, a nélkül, hogy egyet is átugranának.
Ezzel már, azt hiszem, vagyunk annyira, hogy felírhassuk szummaoperátorunkat.

Logikus és természetes, hogy az alsó határt a szumma-parancs alá írjuk, a felsőt pedig fölé. Középen meg lehet jelölni, de nem kell, hogy melyik a «futó» mennyiség. Ez után következik az összegezendő kifejezés szerkezete, alakja, általános számokból alakult indexekkel és kitevőkkel. Természetesen két, három, négy, öt vagy esetleg még több általános szám is szerepelhet a szummajel mellett s mindegyiknek lehet indexe vagy kitevője, vagy mindkettő. (Más lehetőséget itt szándékosan nem említünk.) Ugyanannak a számnak is lehetne indexe és kitevője. Ez azt jelentené, hogy az illető általános szám értéke változik ugyan, ám kitevője valamilyen szabály szerint nő vagy csökken. De hogy a túlzottan elvont tárgyalásmódot elkerüljük, tudván, hogy a szummaparancs eleinte jelentős nehézségeket okozhat, számoljunk végig néhány többé-kevésbbé bonyolult példát. S jegyezzük még meg, hogy a szummaparancs megbecsülhetetlen mértékű egyszerűsítést jelent a számolásnál, mert lehetővé teszi más módon alig leírható kifejezéseknek egyetlen jellel való feljegyzését.
Legyen a


Természetesen a "kifejtésnél" nagyon kell figyelni. De a szükséges figyelem és a nehézség sem a matematikában, sem az életben nem azonos.
Vegyünk most a gyakorlatból egy esetet. Hogyan írunk egy négyjegyű tizedestörtet? Természetesen így:

Az első eset kifejtése:
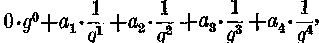
a másodiké: 0*g0+ a1g-1 + a2g-2 + a3g-3 + a4g-4 kettő szemlátomást ugyanazt jelenti. Mégpedig 0 egyest, a1 tizedet, a2 századot, a3 ezredet, a4 tízezredet.
A határokat természetesen másképpen is megadhatom. Ha esetleg n jegyű tizedes törtet akarok felírni s ennél az n még határozatlan, de véges szám, akkor ezt írom:
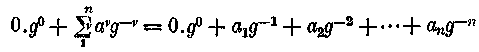
A határokat még merészebben is megállapíthatom. Mondjuk végtelen tizedes tört esetén, vagyis ha a törtnek mindig újabb és újabb jegyei következnek:

Végül megpróbálunk még felírni új parancsunk segítségével valamely helyértékrendszerben, legáltalánosabb alakban felirt számot. Megjegyezzük, hogy miként a legtöbb hasonló esetben, itt is többféleképpen lehet a kifejezést fel-mi. Válasszunk tehát valamely könnyen érthető módot. A helyértékrendszerben írt szám =


Új algoritmusunk, amelynél a számok szokásos írásmódjára való tekintettel látszólag értelmetlenül választottam meg az alsó és felső határt, a következő eredményt szolgáltatja :
1. Mindegyik a,g csoportban az a indexe ugyanaz, mint a g kitevője.
2. Mindkettő az egészszámokon fut végig, +m-től kezdve csökkennek 0-ig és onnan a negatív számokon át —∞-ig.
De ne hatoljunk túlságosan mélyre, mutassunk inkább egy egészen különös, bár gyakran használt írásmódot, amellyel még «alternáló» sorokat is felírhatunk Ezeknél a tagok előjele szabályosan váltakozik. Próbálkozzunk talán a híres Leibniz-sorral:

s írjuk fel tetszés szerinti, de páros tagszámra. A következő írásmóddal valósítjuk meg szándékunkat: közelítő értékben
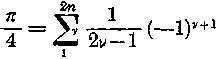
s megvizsgáljuk, hogyan működik algoritmusunk.

Hibátlanul megkaptuk a Leibniz-sort. Meg kell jegyeznünk, hogy 2n a páros számot jelenti. Mert bárhogyan választjuk is az egészszámú n-et (esetünkben más, mint egészszám, nem is jöhet tekintetbe), kétszerese biztosan páros szám. Ha n=2, úgy 2n=4. Ha n=27, akkor 2n=54 stb. Ezért 2n+1, amely a 2n-edik tagban szerepel, páratlan szám. Ez is kitűnően beleillik algoritmusunkba, hisz minden páros sorszámú tag mutatója páratlan szám, pl. a 4. tag mutatója 5. Varázsjelünk kifogástalanul működik és még megelégedéssel látjuk azt is, hogy a látszólag jelekkel kifejezhetetlen, szabályos előjelváltozás követelményét is milyen egyszerűen ki tudtuk fejezni azáltal, hogy a hatvány tulajdonságait felhasználtuk. Negatív számok hatványai páratlan kitevőnél mindenkor negatív értéket adnak. (A parancsok «összekapcsolásának» szabályaiból következik: —a3)=(—a)(—a)(—a) és (—a)6 = (—a)(—a) (—a)(—a) (—a) (—a).Ha a mínusz előjel szorzásban páros számban fordul elő, az eredmény pozitív, különben negatív.) De hogy semmi egyéb ne változzék, csak az előjel ugráljon ide-oda, (—l)-et választottuk alapnak. Bizony ravasz eljárás!
Bármennyire csábító volna is ezt az algoritmust, melynek további tanulmányozását nagyon ajánljuk, alaposabban átvizsgálni, hiszen még csak egészen kis részét láthattuk, mégis át kell térnünk már végre tizedestörtjeinkre. Még pedig példák kapcsán. Feltesszük, hogy csak redukált törtekkel foglalkozunk, azaz olyanokkal, amelyeknek abszolút értéke kisebb mint 1 és a számlálójuknak és nevezőjüknek nincs közös osztója. De sajnos, halmozódnak az új kifejezések. "Abszolút" értékről beszéltünk, ezt a kifejezést tehát gyorsan meg kell magyaráznunk. Nyilvánvaló, hogy a kisebb, mint 1, kifejezés kétfélét jelenthet. Először azt, amit általában ezen értenek.
Vagyis 1/2 kisebb mint 1,(4/7) kisebb mint 1. Általában minden valódi tört kisebb mint 1, hisz éppen azt neveztem valódi törtnek, amelyiknek ez a tulajdonsága. De van a «kisebb, mint 1»-nek még másik jelentése is. Ez utóbbi a negatív számok bevezetésével keletkezett. A 0 bizonyosan kisebb, mint 1. Még kisebb azonban a (—1), (—2), (—3) stb. és általában valamennyi negatív szám.
Akinek adóssága van, annak biztosan kisebb a vagyona, mint azé, akinek egy zechinója van. De éppen e második jelentés miatt nem állíthatom, hogy csak a valódi tört kisebb, mint 1. Éppen ezért minden szám nagyságára három esetet különböztethetek meg. Értékét pozitív értelemmel, negatív értelemmel és végül számértékét magában véve, vagyis abszolút, előjeltől mentes értékét. Ez utóbbi esetben a számot két függőleges vonás közt írom és kijelentem: |5| biztosan nagyobb, mint |3|, mind a mellett, hogy —5 bizonyosan kisebb, mint +3, sőt kisebb még, mint —3. Az abszolút szám mindenkor kisebb, mint |1| és ugyanígy minden más valódi tört abszolút értéke is kisebb, mint 1.
E közjáték után már munkához láthatunk. Megkíséreljük először megállapítani, hogy mennyi lehet a 3/400 tört értéke. Osztással a 0,075 értéket kapjuk, tehát úgynevezett véges tizedestört áll előttünk. Ugyanígy a 4/125 esetében is, lévén ez tizedestörtben 0,032. Minden gyerek tudja, hogy 1/2 = 0,5 és 1/5 =0,2. Ha most elfogadom az általánosan szokásos írásmódot és a redukált tört számlálóját p-vel, nevezőjét q-val jelölöm, akkor érvényes a szabály, hogy csak az a közönséges tört alakul véges tizedestörtté, amelyiknek nevezője, q csak a 10 alapszám 2 és 5 törzstényezőjéből áll.
40=2*2*2*5=23*5, 125=5*5*5=2053, (A hiányzó tényező 0-dik hatványát az általános szabály fenntartása céljából írtuk ki.) 2=21*5°, 5=2°*51.
Minden példánkban érvényesül ez a szabály. Tehát általánosan is állíthatjuk, hogy csak akkor remélhetjük, illetve vehetjük bizonyosra azt, hogy egy osztás «kijön», ha az osztó és osztandó valamennyi közös tényezőjével megtörtént rövidítés után az osztó csakis a 2 és 5 hatványainak szorzatából tevődik össze. A 2 és 5 természetesen a 0 hatványon is szerepelhet, ami egyértelmű azzal, hogy egyáltalán nem szerepel tényezőként.
Ha tehát kiszámítom, tegyük fel 227*513 értékét, vagy általában a 2n*5m számot, meg lehetek győződve, hogy minden racionális szám ezzel a 2n.5m-el osztva valamely zárt egész vagy véges tizedestörttel kifejezhető hányadost ad. Tehát minden
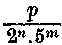
Írásban
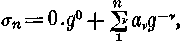
Ha a p/q tört nevezőjének csupa olyan tényezője van, amelyekkel a rendszer alapszáma nem osztható (tehát a tizesrendszerben a 3, a 7, vagy a 3 és a 7 esetén), akkor az osztás eredménye úgynevezett tiszta szakaszos tört lesz. Egy számjegy, vagy a számjegyek csoportja a végtelenségig ismétlődik, 1/7 például =

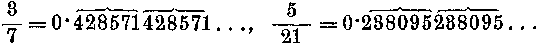
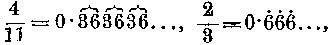
szerint az ismétlődő számjegy, vagy az ismétlődő csoport két szélső számjegye fölé pontot teszünk. Az utóbbi esetben szokás az ismétlődő csoport fölé vízszintes vonalat is húzni. Tehát 7,3 jelentése 7,3333333.... és így tovább, 0,5432189 vagy
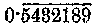
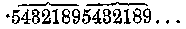
Végül fennáll még annak a lehetősége is, hogy a nevező (osztó) tartalmaz ugyan a rendszer alapszámával közös törzstényezőket, de tartalmaz olyan más tényezőket is, amelyeknek nincs közös osztójuk a rendszer alapszámával. Tizesrendszerben ilyen osztó a 6, tényezői 2 és 3, 5/6-nak megfelelő tizedestört a következő : 0,83333..., tehát a törteknek olyan típusa, amellyel eddig még nem találkoztunk. Neve "vegyes szakaszos tört". Először jön a 8 és csak azután kezdődik a szakasz, a 3. ,A keveredés itt nagyon egyszerű. De megeshet az is, hogy mind a szakaszt megelőző csoport, mind maga a szakasz több számjegyből áll.

a szakasz előtti csoport egyjegyű, a szakasz maga kétjegyű.


Az osztónak, nevezőnek másféle összetétele azonban nincs. Teljes joggal megállapíthatjuk tehát, hogy közönséges törteknek valamely számrendszerben írt törtekké való átalakításánál (vagyis két szám osztásánál) csak véges, vagy tiszta szakaszos, vagy pedig vegyes szakaszos tört keletkezhetik.
Irracionális szám, vagyis olyan rendszertört, amelynél szabály nélkül, vagy az eddig ismertetett szabályoktól eltérő szabályosság szerint követik egymást a számjegyek a végtelenig, osztás eredményeként el nem képzelhető. Ilyen csak gyökvonás műveletéből (tört kitevőjű hatványokkal végzett műveletekből) vagy bizonyos csökkenő hatványsorok összegezésénél vagy más csökkenő sorok összegezésénél keletkezhetnek.
Bizonyosak lehetünk tehát abban, hogy minden racionális számok alkotta tört, vagy racionális számokkal végzett osztás ismét racionális számot eredményez. p/q = r (racionális szám), legyen a p és a q bármilyen, pozitív vagy negatív, egész vagy tört szám, csak irracionális nem lehet egyik sem. De ha így áll a helyzet, akkor feltétlenül lehetséges minden tiszta szakaszos és minden vegyes szakaszos törtet p/q alakú közönséges törtté visszaalakítani. De valamely számrendszerben felírt nem szakaszos, vagy nem periodikus szabály szerint képzett törtet soha sem lehet közönséges törtté visszaalakítani, mert ez esetben irracionális számról van szó és ellenkező esetben sikerülne irracionális számot racionálissá változtatni.
De a «visszaváltoztatás» kiváló próbája lesz eddigi állításainknak. Egyelőre még jóformán el sem tudjuk képzelni, hogy miként lehet végtelen törteket, akár csak periodikusakat is, matematikailag megfogni. Tudjuk ugyan, hogy 1/3 egyenlő 0,33333... (periodikusan ismétlődve a végtelenig), de ha csak a 0,333333... -at látnánk, bizony nem tudnánk, miként fogjunk neki a visszaalakításnak. Legalábbis messzemenő megfontolások nélkül semmi esetre sem.
Biztos, hogy a legegyszerűbb valamely véges törtnek a visszaalakítása. Csak ki kell mondanom és azt, amit mondok, közönséges tört alakjában kell leírnom, máris megvan az eredmény. Tehát 0,225 = 225/1000 és ez 25-tel rövidítve adja a tovább nem rövidíthető 9/40 "redukált alakot". De ha az eredményt szigorúan tudományos módszerekkel kívánom feljegyezni, ezt kell írnom:

Ennél a μ (görög kis m betű) «fut», c a mindenkori együttható (esetünkben a 2, 2 és az 5) és g a rendszer alapszáma (most 10). Az m törtünk jegyeinek a számát jelenti (esetünkben 3). Tehát behelyettesítve:

vagyis ugyanaz, amit józan eszünkkel is megállapítottunk. Képletünknek ezzel szemben megvan az az előnye, hogy minden számrendszerre érvényes és így pontos képét adja a helyzetnek.
Tiszta szakaszos törtek visszaalakítására, a következő képlet szolgál: (A visszaalakítás képleteinek levezetése, hosszadalmas lévén, túlmegy a magunk elé tűzött célon.)

s ez nem jelent egyebet, minthogy a számlálóba a szakaszt kell írni, a nevezőbe pedig annyi kilencest, ahány számjegyből a szakasz áll. Ez a magyarázat a kilencesekkel, természetesen csak a tizesrendszerre érvényes.
Ha 0,3 a visszaalakítandó tört, egyszerűen felírhatom, hogy 3/9 és rögtön megkapom az eredményt: 1/3. Ugyanígy 0,6, az eredmény 6/9, illetve 2/3. A tiszta szakaszos 0,076923 = 76923/999999 alakban írandó fel, rövidítve 1/13 az eredmény. Mindenesetre óvatosan kell a «suszterszabályunkkal» bánnunk, ha csak az általános szabállyal nem ellenőrizzük mindenkor.
Kezdődjék ugyanis a szakasz egy vagy több nullával, akkor a nullákat a számlálóban nem kell kiírnunk, mert egész számot nem kezdünk nullával. De ezeket a «nulla-együtthatókat» a nevezőbe kerülő kilencesek számának megállapításánál gondosan figyelembe kell vennünk. Mivel a szakasz, a nullát beleértve, 6 számjegyből állott, a nevezőben is 6 kilencest írtunk, bár a számlálóban, a nullát elhagyván, csak 5 számjegy maradt.
A vegyes szakaszos törtek visszaalakítása az eddig megismert két eljárásnak bizonyos egyesítése. Ha a tizesrendszer számára megint meg akarom adni a «suszterszabályt», akkor ezt kellene követelnem: «írd a számlálóba egész számként az első szakasz végéig terjedő számjegyeket (tehát mind a szakaszt megelőző nem szakaszosokat, mind a szakaszt alkotókat). Ebből az egész számból vond ki a nem szakaszos, másképp a szakasz előtti számjegyeket. Ezután írj a nevezőbe annyi kilencest, ahány jegyből a szakasz áll. A kilencesek után azonban írj annyi nullát, ahány számjegy a szakaszt megelőzi".
Tegyük fel, hogy a szabályt a 0,22727272727... törtre kell alkalmaznom. Akkor ezt kellene írnom:

Látjuk, valamennyi visszaalakítási szabályunk rendesen
rövidítetlen törtekhez vezet és ezeket kell a végleges p/q alakra hoznunk (p-nek és q-nak már nincs közös osztója). De ez teljesen ártalmatlan feladat, hisz bármely középiskola legalsó osztályának minden tanulója hibátlanul el tudja végezni.
Természetesen e harmadik és utolsó esetben is fel tudunk írni a «visszaalakításra» általános, elegáns parancsot. A következőt :
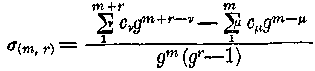
itt m a szakasz előtti számjegyeknek, r a szakaszt alkotó számjegyeknek a számát jelenti, g a rendszer alapszáma, c a mindenkori együttható, v az első összegezési parancsnak, μ a másodiknak a «futó» száma és ezeknek a felső és alsó határai állnak az összegezési parancs fölött és alatt.
Most már uralkodunk a törtrendszerek egész birodalmán és bármely számrendszer törtjét közönséges törtté tudjuk átalakítani.
Írjuk például fel a tizesrendszerben a 0,23471... törtet, és alakítsuk vissza az utóbbi, csak látszatra szörnyű képlet alapján:
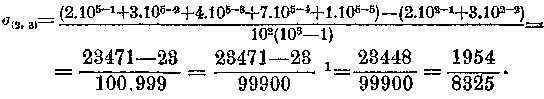
(1 Hasonlítsuk össze a suszterszabállyal.)
Ez az utóbbi példa azt is megmutatja, hogy egyszerűnek látszó vegyes szakaszos tört jelentősen bonyolult közönséges törtnek felelhet meg.
De már jelentős teljesítményekre tekinthetünk vissza. Ismerjük az egész, a tört és az irracionális számok birodalmát. Mindezeket nem csak az abszolút értékük szerint. Ismerünk ugyanis pozitív és negatív számokat is. Sőt mindezeket valamennyi számrendszerben. Sőt tovább : foglalkoztunk általános számokkal is, láttuk, hogy állandókat és ismeretleneket is jelölhetnek. S most, midőn az egy ismeretlenes egyenletek és az úgynevezett diophantosi egyenletek algoritmusát is megismertük, vagy legalább is a lényegüket, kellőképpen érettek vagyunk arra, hogy a matematika legfontosabb témájával, a függvényekkel kezdjünk foglalkozni. De itt már nem álcázva, hanem nyíltan és örömmel lépünk a felsőbb matematika valódi talajára és ismét Leibniz hatalmas szelleme lebeg előttünk. Mert ő volt az, aki a függvény, a funkció fogalmát a 17. század kilencvenes éveiben a maga mélységében és általánosságában felfogta és neki ezt a nevet adta. Oswald Spenglerrel szólunk, ha a függvényt a «fausti», a «napnyugati» számnak nevezzük. Mert éppen ez a «fausti» jelleg az, ami a felsőbb matematikát oly kalandossá, izgatóvá és egyúttal legmélyebb alapjaiban oly könnyűvé teszi.
E helyütt kijelentjük, annak teljes tudatában, hogy állításainkat tényekkel kell majd igazolnunk: minden, ami e könyvben még következik, könnyebb mint az eddigiek! Sokat fogunk ezentúl beszélni, magyarázni, sok mindent fogunk együtt megtárgyalni. De a fáradságos számolgatás, bíbelődés megszűnik s a matematika magaslati levegőjén fogjuk a merész mesterfogásokat, bizarr paradoxonokat és meglepő, szinte felfoghatatlan megoldásokat élvezni.
TIZENNYOLCADIK FEJEZET
Függvények (Algebrai levezetés)
Válasszunk példának egy egyszerű diophantosi egyenletet, legyen ez a következő:
3x—y = (—5)
Oldjuk meg olymódon, hogy megkapjuk az egészszámú megoldásait, tehát az Euler-féle módszerrel. Az eredmény:

Továbbá az y számára a 3n+5 eredményt. Tegyük most az n helyébe 1-től kezdve a számokat.

és így tovább.
Tehát Euler módszere számtalan egészszámú megoldást szolgáltatott. Ugyanígy számtalan negatív megoldást is találhatunk. Mert

és így tovább.
Látjuk, hogy n=(—2) értéktől kezdve, mindkét ismeretlen negatív, hisz x=n lévén, negatív n-nek esetén x is negatív. y is mindig negatív, ha n egész és kisebb mint —1. Mert 3n abszolút értéke már n=—2 esetén is nagyobb, mint az állandó, a +5. Még sokkal inkább ez a helyzet n=—3, tehát y=—9+5 esetén.
Fentiek szerint már két ízben találtuk végtelen sok megoldását egyenletünknek és ezekhez járul még két eset:
egyiknél n=—1, itt x=—1, y=+2 a másiknál n=0 x=0, és y=+5.
Most kissé átalakítjuk diophantosi egyenletünket, de semmi mást nem változtatunk rajta. 3x—y=—5 helyett ugyanis így írjuk:
y=3x+5
Ezt minden további következmény nélkül megtehetjük. Most azután elhatározzuk, hogy nemcsak az egészszámú, hanem a törtszámú megoldások is érdekelnek bennünket. Megállapodunk továbbá, hogy mindenkor az x-et fogjuk szabadon választani, a hozzátartozó y-t behelyettesítve fogjuk kiszámítani. Esetünkben ez az egyszerűbb, mert az y együtthatója 1 és ezért nincs szükség osztásokra, de igaz, hogy itt még nem említett elvi okaink is lehetnének arra, hogy így járjunk el. Keressünk tehát néhány törtalakú megoldást.

és így tovább.
Természetesen y számára egészszámú értékek is adódhatnak, ez az eset x =1/3 -nál be is következett. De bizonyos, hogy az esetek többségében tört x esetén tört y-t fogunk kapni. Ismét számtalan megoldását találtuk, immár nem diophantosi egyenletünknek (nem diophantosi, mivel törtszámú megoldások is érdekelnek). x=—5/3 esetén y=0. Minden —5/3-ál kisebb tört (vagyis a számvonalon messzebb balra eső tört) már negatív y-hoz vezet.
De bizonyos, hogy határozatlan egyenletünk számára már számtalan egészszámú és törtszámú megoldást találtunk. Kibővített számfogalmunk kapcsán eszünkbe juthatna, hogy x helyébe egy vagy több irracionális számot is helyettesíthetünk.
Mondjuk

Így tehát a megoldások végtelenjével állunk szemben és elborzadunk, hogy az ártatlan külsejű
y=3x+5
egyenletünk mennyi megoldást rejt.
De azért, hogy algoritmusunkat, amelynek sokoldalúságát már láttuk ugyan, de jelentőségét még nem foghattuk fel, teljesen át tudjuk tekinteni, szerkesszünk egyszerű gépet és működtessük, legalább gondolatban.
A következő szerkezetet állítjuk össze.
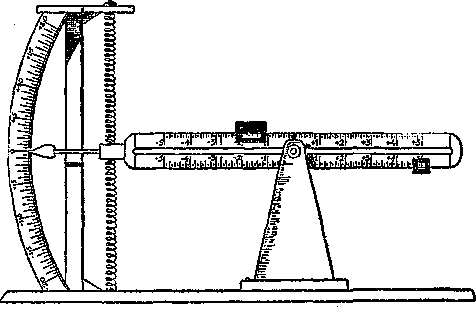
13. ábra.
Egy mérlegszerű szerkezet egyik karjának végére szerelt mutató körívalakú skála számbeosztása előtt mozog. Maga a mérlegkar olyan alakú, hogy alul és felül két futósúlynak pályájául szolgál. A két pályán is pontos számbeosztás van. A pályán mozgatható futósúlyok cserélhetők is. A mechanika legelemibb törvényei alapján tudjuk, hogy esetünkben egy súlynak a hatása nem csak a nagyságától függ, hanem attól is, hogy az «emelőkarnak» melyik részén van éppen. Egy kilogramm súly a kezdő-, forgásponttól mért 5 egység távolságban ötször akkora hatású, mint egy kilogramm 1 egység távolságban. Tudjuk, ez a tizedesmérlegnek is az elve. Még a következőt kell megállapítanunk : a mutató az ívalakú skálán mérlegünk mindenkori megterhelését mutatja meg. Ha a mérleg egyensúlyban van, akkor a mutató a nullára mutat, mert lefelé vagy felfelé történő elmozdulás ellen rugók rögzítik. A rugók szerkezete olyan legyen, hogy húzással szemben nagyon erős ellenállást fejtsenek ki, nyomással szemben viszont nagyon kicsit (elméletileg: egyáltalán semmi ellenállást). Végül még, az alsó pálya az állandó beállítására szolgál, a felső pedig az x-ére. Mindenkor a kilogramm az egységünk.
Most már céljaink szolgálatába állíthatjuk gépünket. Használati módját mintegy használati utasítás alakjában állítjuk össze magunknak. Tegyük fel, hogy szekrényben tárolva, futósúlyoknak egész sorozata áll rendelkezésünkre. Most kiveszünk a szekrényből az
y=3x+5
egyenletünk ábrázolására egy szép egykilogrammos súlyt, ráhelyezzük mérlegünk «állandó» jelzésű pályájára és addig toljuk, amíg középpontjának a jele a skála 5 számával össze nem esik. Erre a célra szolgál a súlynak az úgynevezett «ablaka». Ilyen súlyok minden gyógyszertár személymérlegén láthatók. Tekintve, hogy állandóról van szó, a súlyt a helyén rögzítem. Természetesen csak arra az időre, amíg az
y=3x+5
egyenlet tárgyalásával foglalkozom. Mérlegünkre mostan ez az 1 kilogramm ötször akkora hatást fejt ki, mint ha a skála 1 jelű pontján állna. S ha most semmi egyebet sem állítok be, akkor a mutató az ívskála ötösére kell, hogy mutasson. Mert feltételeztük, hogy a rugókat ily módon méretezték. Most kell az x-et beállítani. De tekintve, hogy nem egyszerűen x szerepel az egyenletben, hanem az x együtthatója 3, kikeresek egy 8 kilogrammos súlyt és azt helyezem a felső pályára, mivel egy kilogramm számunkra az 1 számot jelképezi. De hova toljam ezt a súlyt?
Zavarban vagyok, matematikai alapon kell a dolgot megfontolnom. Ebből azonnal kiderül, hogy x helyébe be kell helyettesítenem, az x-et szabadon választhatom. Tehát felteszem magamban, hogy először azt az x-et keresem ki, amelynél a mérleg egyensúlyban van, tehát amelynél y=0. Minden számolás nélkül, csak próbálgatással rájövök, hogy a kívánt eredményt akkor értem el, ha a 3 kilogrammos futósúly a felső skálának pontosan a -5/3-ot, azaz a — 1 2/3-ot mutató jeléhez ért. Ekkor ugyanis baloldali mérlegkarnak (ezt nevezzük ezentúl negatívnak) a terhelése 3 kilogramm — 5/3 távolságra a forgásponttól, a jobboldali (pozitív) mérlegkar terhelése pedig a +5 távolságra elhelyezett 1 kilogramm.' De mivel továbbá a mechanika törvényei szerint a mindenkori terhelés a súlynak és a forgásponttól mért távolságnak a szorzatából adódik, első esetben a terhelés 3*(-5/3), a másodikban pedig 1,5=5 vagyis abszolút értékre egyformák. De mert mérlegünkön egyensúly akkor áll fenn, ha a pozitív és a negatív terhelés abszolút értéke egyforma, eredményünk szemmel láthatóan igazolja, hogy az
y=2x+5
egyenletben x-et -5/3-nak kell választanunk, hogy y nulla legyen.
Már említettük, hogy az állandót nem szabad semmiképpen sem változtatnunk. Mégis gépünkön más, elegánsabb módon is beállíthattuk volna. Ha ugyanis meggondoljuk, hogy az y=3x+5 egyenletet ilyen formában is írhatnánk:
y=3x1+5x0
minthogy minden nulladik hatvány értéke 1, tehát egyenletünk az ilyen írásmód következtében mit sem változnék és ezután a felső pályát az x1, az alsót pedig az x° helyének tekintve, az 5 az x0 együtthatójaként fog szerepelni. De ez esetben vehetünk egy 5 kilogrammos súlyt is, megerősíthetjük az alsó pálya 1 jelénél és ez ott is maradhat, mert x° minden x értéknél egyaránt 1 lévén, 5x° mindenkor az 5*1=5 értéket adja. Itt ez még mellékes. De még visszatérünk erre.
Mi azonban most megelégszünk az első változattal, vagyis azzal, hogy 1 kilogrammot erősítettünk az 5 jel mellé. És megjegyezzük továbbá, hogy az állandóval többé nem törődünk, mert mostani egyenletünk szempontjából mintegy a mérleg alkatrésze lett és önállóan fejti ki hatását.
Annál jobban izgat a másik súly, kísérletezni szeretnénk vele. De a súlyon látható jelzővonal-mutatta érték a mindenkori x-et jelenti, rajtunk múlik, hogy hová toljuk mozgási határain, a +5-ön és a —5-ön belül. De helyzetváltozás az emelő karok törvénye szerint terhelési állapot változást is jelent. Kísérletezzünk tehát. Toljuk a 8 kilogrammos futósúlyt, mondjuk, az x = 1 2/5 = 7/5 jelre. A jobboldali mérlegnél azonnal süllyedni kezd, a skálán mutatott y érték változik. Néhány lengés után a mutató megállapodik a 9 1/5 értéken. Az egyenlet szerint valóban y = 9 1/5 , mivel 3(7/5)+5 = (21+25)/5 = 46/5 = 9 1/5.

14. ábra.
Ha tehát az x-et önkényesen változtatjuk, gépünkön vele változott az y is. Így egyelőre egészen pontatlanul csak annyit állapítunk meg, hogy az egyik ismeretlen önkényes, független változásától szükségképpen függ a másik változása. Ha pedig a "változó ismeretlen" és hasonló kifejezések helyett röviden «változót» mondunk, akkor állíthatjuk, hogy a "független változó", az x, minden változása, maga után vonja a "függő változó", a "függvényt", az y változását. Ennek az összefüggésnek, törvénynek, a neve "függvényt". Gépünk eddig magától szolgáltatta az eredményeket, mivel ezt a törvényt állítottuk be rajta. De a törvény nem volt más, mint az egyenletünk,
y=3x+5.
És éppen ezt az «egyenletet» ebből a szempontból függvénynek nevezzük. Általános alakját Leibniz szerint így írjuk: y=f(x) és így mondjuk : y függvénye x-nek, vagy y egyenlő funkció x. S ez nem jelent mást, mint hogy y értéke valamilyen összefüggésben van az x értékével.
Foglaljuk tehát még egyszer össze: az
y=3x+5 vagy általánosan y=f(x)
függvényben az x a független változó, y pedig a függő változó, amelyet kissé megtévesztő módon szintén függvénynek szokás nevezni, x és y együtt a változók.
Most, hogy már valamelyest megismertük a függvénytan kifejezéseit, térjünk vissza gépünkhöz, függvény-kiszámító szerkezetünkhöz és végezzünk vele újabb kísérletet. Toljuk el valamelyest a 8 kilogrammos futósúlyt az x pályán mostani helyéről és figyeljük meg, mit jelez közben mutatónk az y skálán. Látjuk ekkor, hogy folytonosan mozgott közben. Végül is megállapodott a beosztás két vonala között. De a futósúlyunk se áll pontosan a pályája valamelyik beosztással jelölt helyén.
Gépünkkel mostan más mutatványt akarunk bemutatni. Azt állítjuk, hogy a pályánk a számvonal. De mivel már tudjuk, hogy a számvonal megszakítás nélkül, folytonosan tartalmazza valamennyi egész és tört, valamint irracionális számot, így minden folytonos eltolás egyaránt azt jelenti, hogy az x, eltolás közben, a rendelkezésre álló kereteken belül valamennyi lehetséges értéket felveszi. Tehát mind az egész-számúakat, mind a tört és irracionális értékeket.
A folytonosság fogalma a függvénytanban igen nagy szerepet játszik, különösképpen a nagy matematikus, Weierstrass felfedezései óta. De egyelőre megelégszünk azzal, hogy utaltunk erre a fogalomra, annál inkább, mivel mi geometriai úton sokkal világosabban tudjuk tárgyalni és megmagyarázni.
A függvényekre vonatkozó eddigi tudásunkat inkább egy másik feladat megoldására használjuk fel, amelynek értelmét és célját azonban nem tudjuk egyelőre felfogni. De mivel ez a feladat felettébb egyszerű, nem látjuk semmilyen okát sem annak, hogy ne foglalkozzunk vele.
Feltesszük tehát a kérdést, hogy mi történik az y mutatóval, ha az x értékét valamely helyen egy bizonyos értékkel növeljük. Valószínűnek látszik, hogy a mutató is bizonyos, meghatározott értékkel fog elmozdulni. De minthogy már egyszer euklidesi módon megállapítottuk, hogy mennyiségek viszonya független nagyságuktól, így a változás látható mértékéül felhasználhatnánk az x növekményének és a belőle következő y növekménynek a viszonyát. S ha továbbá, teljesen általánosan, az x-nek valamilyen helyen bekövetkezett növekedését, növekményét tekintjük, akkor természetes, hogy a hozzátartozó y növekmény is "valamilyen helye" vett növekmény lesz. Ugyanúgy, mintha a pályát és az y skálát nem láthatnék.
Tehát «valamely x» vagy másképpen «az x» — hisz ez utóbbi is ugyanazt jelenti, tekintve, hogy az x értékét nem rögzítem — véges értékkel növekszik. Ezt a véges értéket Δx-szel jelölöm. A háromszög (Δ) a görög nagy D betű (neve delta). Minden gyermek ismeri mint a Nílus-delta jelképét. Az x-et a deltánk után írom annak jelölésére, hogy az x növekményéről van szó. Az eddig megismert függvények törvényeiből következik, hogy az y-mutató is kilendül helyéből. Ezt az elmozdulást Δy-nal jelölöm. Természetesen csak akkor, ha a mérlegen a tárgyalandó függvénynek megfelelő a beállítás, vagyis az alsó pályán a 1 kilogramm az 5 ponthoz rögzítve, a 3 kilogrammos súly pedig valahol a felső pályán tartózkodik.
Algebrai nyelven a kérdés most a következő: hogyan viszonylik a mérlegen beállított függvény esetén a Δy a Δx-hez ? Másképpen: milyen Δy következik szükségképpen az x-nek Δx-szel történt megváltozásából?
Ne törjük a fejünket, álljunk neki és számoljunk. Ha növekményünket alkalmazni kívánjuk egyenletünkben, akkor ezt kell felírnunk :
(y+Δy)=3(x+Δx)+5
Mert az x-ből növekedése után (x+Δx) lesz s ebből következik, hogy az y-ból (y+Δy).
Ismételjük, most már szinte fölösleges módon: nem tudjuk, mennyi az x. Azt sem tudjuk, mennyi a Δx. Csak az a kívánságunk, hogy az értéke véges legyen. Mellesleg megjegyezzük: bármekkora lehet. És csakis a következők könnyebb megértése okából tekintjük kicsinek. Tehát
(y+Δy) = 3(x+Δx)+5
Keressük Δy : Δx, vagyis Δy/Δx értékét. Más szóval a Δy-nak és Δx-nek a viszonyát. Végezzük el a szorzásokat, hogy végre megszabaduljunk a zárójelektől.
y+ Δy = 3x+3Δx+5.
Most olyan mesterfogást alkalmazunk, amely még Leibniztől származik. Igaz, ő más formában írta. Emlékezzünk vissza, y=3x+5, tehát levonhatjuk az egyenlet mindkét oldalán ezeket az egyenlő mennyiségeket, s ezzel semmi sem változott. Az almákkal és a súlyokkal foglalkozó első példánk ilyen művelet jogosságát kellőképpen igazolta. Tehát:
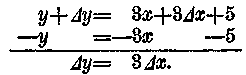
De ha Δy=3Δx, akkor ebből azonnal következik, hogy
Δy : Δx = 3Δx : Δx,
vagyis
Δy/Δx = 3;
aránylatnak írva pedig
Δy : Δx = 3 : 1.
Megoldottuk feladatunkat. Tudjuk, hogy a viszony értéke független az összehasonlított mennyiségek nagyságától, tehát ezért a Δy és Δx tetszés szerint kicsinek tekinthető, a nullát megközelítő kicsinek. A matematika nyelvén azt mondhatnám, hogy a futósúlyt csak a legközelebbi irracionális számig tolom el. A számvonal tanulmányozásánál tudjuk meg, hogy milyen hatványozottan kis eltolást jelent ez. De az x ilyen rendkívül kis növekményének már nem Δx a szokásos jele, hanem dx, a hozzá tartozó Δy jele ugyancsak dy. Tehát ezt írjuk:
dy/dx=3.
Most már leleplezzük az egész eljárást: minden különösebb nehézség nélkül meghatároztuk a rettegett "differenciálhányadost". És azt mondhatjuk, hogy az y=3x+5 függvény "differenciálhányadosának" az értéke 3. Másképp
dy/dx = 3, vagy y' = 3. Az y' jelentése dy/dx, vagyis az y=f(x) függvény «első» differenciálhányadosa, tehát olyan függvénynek, amelyben az y az x független változónak valamilyen kifejezésétől függ.
Most látjuk, hogy ominózus "differenciálhányadosunk" mindenütt egyforma. Akárhol növelem is az x-et a nagyon kis dx értékkel, a dy viszonya dx-ünkhöz mindenkor 3, azaz 3:1 marad. Az állandó itten semmilyen szerepet sem játszott. Ha elhagyom, akkor ezt kapom:

levonjuk az alapegyenletet

Azt, hogy ez miért van így, később látjuk meg. De gépünk alapján tulajdonképpen érthető is. Hiszen az egyensúly megbontása (Ha az 5 kg súly «tehetetlenségétől» eltekintünk) csakis a 3 kilogrammos x súly eltolásának a következménye. És ez mindenütt egyformán következett be. A «differenciálhányados» tehát a függvény változásának az x minden értékére egyaránt érvényes törvénye.
Új algoritmusunknak, a "differenciálszámításnak", amelyet csak külsőségekben megnyilvánuló kabbalának ismertünk meg egyelőre s csak egészen kis részét tudtuk megragadni, további alkalmazását fogjuk megkísérelni. Egészen merészen, mert a számunkra teljesen új négyzetes, "kvadratikus"
y=2x2+7
függvényt fogjuk az imént megismert módon vizsgálni. Gépünkkel most már egyáltalán nem törődünk és teljesen rábízzuk magunkat a megismert eljárásra. Szkémánk szerint ezt kell tennünk:
y+Δy = 2(x+Δx)2+7.
Mivel (x+Δx)2 értékét nem tudjuk közvetlenül felírni, nehézkesen (x+Δx) (x+Δx) szorzásnak fogjuk tekinteni és így számítjuk ki. Az eredmény [x2+xΔx+xΔx+(Δx)2], azaz x2+2xΔx+(Δx)2.
Most alkalmazzuk a fogást:

Az így kapott eredményből eddigi eljárásunkkal nem tudjuk a Δy és a Δx viszonyát meghatározni. Számoljunk tehát valamelyest. Mondottuk, hogy végeredményben minket nem az úgynevezett "differenciahányados" Δy/Δx érdekel, hanem a "differenciálhányados" Δy/Δx. De ennél a dx már biztosan
rendkívül kis szám. Ha ezt a rendkívül kis számot egészen durván valamilyen törtnek képzelem el, akkor, a q természetesen csak óriási nagy lehet, hatványozva

Δy=4xΔx+2(Δx)2,
már csak ennyit írunk *
dy= 4xdx
és a végeredmény
dy/dx = 4x
Itt a kvadratikus függvénynél egészen különös dolgot tapasztalunk. A változás törvénye már nem mint puszta szám mutatkozik, hanem függ az x-től; tehát az x mindenkori értékével együtt változik a kiszámított értéke. Tehát, itt, azt mondhatnánk, maga a változás is változékony. Igaz ugyan, hogy szigorúan a 4x : 1 viszony megszabta módon.
Az eddigi módszerrel, szigorúan szabályokhoz kötött módon levezethetnénk a differenciálszámítás teljes algoritmusát. Matematikai pontosságunk csak nyerne ezzel. De mivel a kezdő számításmódunk minden problémáját jobban át tudja tekinteni, ha képszerűen látja a dolgokat maga előtt; tekintve továbbá, hogy kalkulusunk történelmi fejlődése is majdnem kizárólag geometriai alapon nyugodott, hagyjuk most szintetikus előadásmódunkat, hisz ez pszichológiai szempontból is előnyös lesz és szerezzük meg új számításmódunkhoz és az egész végtelenanalízis tanulmányozásához nélkülözhetetlen geometriai alapismereteket.
TIZENKILENCEDIK FEJEZET