x = 27/9 = 3.
Az apa 30 éves volt, a fiú 3, amidőn az apa 10-szer olyan idős volt mint fia. Ez helyes, szemmel láthatóan. De az is kérdés, hogy hány éve történt ez az esemény, ha az apa ma 48 éves. Kivonunk, 48—30=18 és azt feleljük, hogy 18 éve. A fiú akkor 8 éves volt.
Egyébként az egyenletet azonnal úgy is felállíthattuk volna, hogy x közvetlenül azt a számot jelentse, ahány éve az apa tízannyi idős volt mint a fia. Akkor így kellene következtetni: az apa most 48 éves. Tehát (48—x) éves korában volt 10-szer olyan idős mint a fia. De mivel a fiú ma 21 éves, és számára is x éve történt az esemény, tehát akkor (21—x) éves volt. Az egyenletünk tehát
(48—x)=10(21—x) vagy (21—x)= 1/10 (48—x).
Oldjuk meg az első egyenletet: hisz a két egyenlet azonos.
(48—x)=10(21—x)
48—x=210—10x
9x=210—48
9x=162
x= 162/9 = 18
Van még egy harmadik módja is a feladat megoldásának. Minthogy az apa 27 évvel idősebb fiánál, 27 éves volt akkor, amikor fia 0. Ebben az időben született. Most már az apa korának 1/9-ével kellett, hogy öregedjék, hogy fiát tízszeresen felülmúlja. Mert ha a kilenc egyenlő részhez egy tizediket fűznek, éppen tíz rész adódik.
Másképpen mondva 9/9 + 1/9 = 10/9 tizede azonban 1/10 ∙ 10/9 = 1/9, mert tízszer 1/9 = 10/9. Így, minthogy 27 kilencede három év, az apa, fia születése után 3 évvel, 30 éves korában, lett tízszer olyan idős mint hároméves fiacskája.
Csupán azt akartuk bemutatni, mennyi változatosságot, tárgyalási lehetőséget nyújt még egy ilyen egyszerű példa is és mennyire fontos már itt is a számoló ügyessége, a legvilágosabb és legelegánsabb megoldás megtalálása szempontjából. Olvasóinknak is nemsokára meg lesz az érzékük a matematikai pontosság és elegancia megítélésére. De mégegyszer: itt kezdődik a művészet és itt kell automatához hasonlóan gyakorolni.
Még csak egy szöveges példát akarunk ideiktatni, amely úgyszólván klasszikus nevezetességre tett szert. Ez az úgynevezett "Diophantos sírköve". Diophantos alexandriai matematikus volt, aki a Kr. u. IV. században élt. Zseniális matematikus, talán az egyetlen a maga nemében a görögök közt. A többi inkább geometer volt. Annyi bizonyos, hogy elsősorban ő fejlesztette ki az egyenletek elméletét, és jelentős hatással volt az arabok és a középkor matematikai tudására. Monda szerint sírkövének a következő volt a felirata:
Ím ezen emlékmű Diophantos hamva fölött áll
Élte korát adják művei és ez a kő.
Ifjúként tölté hatod éltét isteni kegyből
Még tizenketted után, gyenge szakálla kiüt.
Egy heted élttel utóbb nászfáklyák égtek előtte
Öt évvel azután, kis fia megszületett.
Ó, boldogság nélküli ifjú, félig el érték
Évei atyja korát s lett hona szürke Hades.
Még négy esztendőn a tudás könnyíti a gyászát
S hosszú élet után, őt is elérte a vég.
A szép patetikus disztichonoktól a hűvös matematikához visszatérve, megállapítjuk, hogy Diophantosnak előttünk egyelőre ismeretlen hosszú élte (x-nek nevezzük) fokozatosan, élete részeiből és többletévekből, tehát állandókból, tevődik össze.

A törtek közös nevezője 84, mert 84-ben úgy a 6, mint a 12. mint a 7 és a 2 megvan. Így írhatjuk :

Az egyenlet mindkét oldalát most megszorozhatjuk 84-gyel, ezáltal valamennyi tört nevezője eltűnik. Marad:
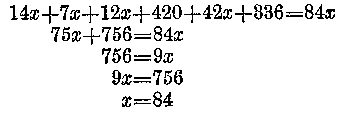
Diophantos tehát 84 éves lett. Tizennégy évig volt gyermek, 21 éves korában nőtt ki a szakálla, 38 éves korában megnősült, 38 éves mikor fia születik, aki 42 évig, tehát Diophantos 80 éves koráig élt. Gyászolva tölti a hátralevő 4 évet haláláig, amely 84 éves korában következett be.
TIZENNEGYEDIK FEJEZET
Határozatlan egyenletek
Nem minden szándékosság nélkül idéztük Diophantos szellemét. Ez a nagy matematikus tekinthető az egyenletek egyik különleges fajtájának, a határozatlan, diophantosi egyenletek felfedezőjének. Az a körülmény, hogy mennyire
jogosult az egyenleteket őreá visszavezetni, legalább olyan «határozatlan», mint az egyenletei. Ránk maradt írásaiból a matematika történetének kutatói szerint nem derül ki olyan adat, ami ezt a feltevést alátámasztaná. De mert a név már meghonosodott, tartsuk meg mi is.
Ugyan mik ezek a kétszeresen is talányos «diophantosi» egyenletek?
Ezúttal szavakba foglalt feladattal kezdjük és e fontos egyenletek lényegét és kezelési módját együtt fogjuk felfedezni. Kérdezzük tehát: melyek azok a számok, amelyek egyikének nyolcszorosa a másik háromszorosával növelve összesen 91-et ad?
Olyan ez a kérdés, hogy eddigi tanulmányaink alapján nem tudunk rá válaszolni. Mert azonnal észrevesszük, hogy itt nemcsak egy ismeretlen x szerepel, hanem két ismeretlent kell meghatározni, amelyeket az x és y betűkkel szándékozunk jelölni. Felírhatjuk tehát:
8x+3y=91.
De ezek után mit csináljunk? Szabályaink szerint 8x=90-3y és x=(90-3y)/8, vagy 3y=90-8x és y=(90-8x)/3.
Egész természetes, hogy így nem jutunk tovább. Mert az egyik ismeretlent mindig csak a 91 és a másik ismeretlennel fejezzük ki. Valamilyen szerencsés sugallat alapján kipróbálom az x=5 és y=17 értékeket. Valóban: 8∙5+8∙17= 40+51=91. Ez tehát megoldás. De nagymértékben rosszallom, hogy nem az egyetlen. Itt is algoritmust kell tehát keresnünk, kabbalát, hogy az vezessen csalhatatlanul célhoz. De még egy mellékfeltételt is meg kell említenünk. Határozatlan, diophantosi egyenletek megoldásaként csak egész számokat fogadunk el. Különben már eleve végtelen sok megoldásunk volna. Nem kellene egyebet tennünk, mint x-et valamilyen tetszésszerinti számmal, mondjuk 7-tel egyenlővé tenni és a következőket kapnánk:
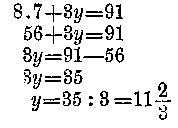
Az egyenletet x vagy y megválasztásával mindenkor, feltétlenül, egyértelműen megoldható, egy ismeretlenes egyenletre vezethetném vissza. Mert ismeretlennek tetszés szerinti megválasztása nem jelent kevesebbet, mint hogy az egyik ismeretlent ideiglenesen, adott esetre konstánssá változtatom.
Azt követeljük tehát, hogy a megoldás mindkét ismeretlenre egész számú értékeket szolgáltasson. De ez a követelés nem teljesíthető minden két ismeretlenes egyenletnél. Erről azonban csak később.
Még mielőtt közelebbről megismernénk azt a zseniális megoldási módot, amellyel Leonhard Euler bennünket megajándékozott, még egy igen gyakori matematikai mesterfogást kell megtanulnunk, amelynek nagyon nagy szerep jut a módszerben. Ez a mesterfogás a «helyettesítés», a "szubsztitució".
Lássunk egy konkrét példát. Senki sem állítja, hogy a következő egyenletnek

túlságosan bizalomgerjesztő a megjelenése. De ha közelebbről megvizsgáljuk, kiderül, hogy benne az (x-4)/3 kifejezés állandóan ismétlődik és az x is egyedül és kizárólag ebben a kifejezésben szerepel. Ezt a kifejezést, (x-4)/3 , szinte új ismeretlennek tekinthetem és úgy kezelhetem, mintha (beszédmodorunk szerint) alma lenne. Jelölje immár ezeket az almákat az n betű, akkor írhatjuk, hogy
2n+3n—4n=9—2n.
Azzal, hogy az n mit jelent, egyelőre nem törődöm. Nem kérdezem, hogy részletesen mit tartalmaz az alma, hány magja van, szára és csutkája, hanem megbízom a magasabbrendű algoritmusban és először azt igyekszem megállapítani, hogy milyen szám tartozik egy almához. Csak később fogom az alma részleteit közelebbről megvizsgálni. Új egyenletünk, amelynek az n az ismeretlene, a következőt adja:
2n+3n—4n+2n=9 ; vagyis 3n=9 és n=3. De most tudom, hogy én magam vezettem be az

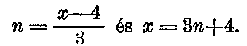
Itten, mint már mondottuk, n=3. Tehát x=9+4=13. Az olvasóra bízzuk az egyenletnek segédismeretlen helyettesítése nélküli közvetlen megoldását. Bizonyos, hogy e próba, vagy az x=18 helyettesítése igazolja eljárásunk helyességét.
Most már gyakorlatból tudjuk, hogy mi a «helyettesítés». Valamely bonyolult felépítésű kifejezésnek egyszerűbb elnevezése. Legalább is a mi tudományunk jelenlegi fokán. A felsőbb matematikában, különösen pedig az integrál-számításban, ahol a helyettesítések nélkülözhetetlen és döntő szerepet játszanak, megeshet, hogy valamely egyszerűbb kifejezés helyettesítendő bonyolultabbal. Egyébként már magunk is tudunk ilyen esetekről. Ha valahol, valamilyen okból 1 helyett mondjuk 150 kifejezést írjuk, vagy valamely, mondjuk, b betűt b1b0-ból keletkezettnek tekintünk, akkor ez már egyszerűt bonyolulttal helyettesítésnek egy esete. Még ha nagyon különleges eset is. De, hogy állításaink általános érvényét kellőképpen megőrizzük, azt kell mondanunk, hogy "helyettesítésen", "szubsztitución" valamely kifejezésnek másikkal való pótlását értjük. Természetesen nem vaktában. Biztos, hogy x-et nem szabad u-nak mondani. De x helyett mindenütt írhatunk u-t, ha nem hanyagoljuk végül el a
"feltételi egyenletet", hogy x éppen u-val azonos, vagyis x=u. x helyett mindenütt 2u-t is írhatok. Vagy u/2-t, vagy pedig u/250-et. Az x akkor végül az u-nak kétszerese, fele vagy 250-ede.
Helyes, láttuk, hogy helyettesítéssel bonyolult számítások egyszerűsíthetők. De min alapszik tulajdonképpen az, hogy egyáltalán helyettesíthetek? Logikai szempontból a dolog egyszerű. Az


alapvető feltétele! Matematikai nyelven azt mondjuk, hogy itt az izomorfizmusnak, alakegyenlőségnek az esete forog fenn. Az egyenlet szerkezetét, alakját vagy az elvégzendő műveleteket a helyettesítés nem érintette és az együtthatók, valamint a parancsok változatlanok maradtak. Algebrai szempontból több egyenletből álló rendszerrel van dolgunk, egyik közülük az alapegyenlet, a másik pedig feltételi egyenlet. Így:

és
De ezzel sem foglalkozhatunk tovább, hogy végre a diophantosi egyenleteinkhez jussunk. Tudjuk már, hogy közben helyettesítések különleges fajtájával lesz dolgunk és a "feltételi egyenletek" más követelményekkel is kiegészülnek. Előbbi példánkat kissé változott formában
3y+8x = 91
ismét felírván, Euler módszere szerint először az egyik ismeretlent ki kell a másikkal fejeznünk. Gyakorlati szempontok azt kívánják, hogy a kisebb együtthatójú ismeretlent fejezzük ki a másikkal. Itt y-t az x-szel. Következőket kapjuk :
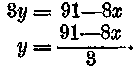
Ez az első lépés. Most — Euler szerint — a törtet, áltörtnek tekintve, bontsuk szét egész és tört részre. Tehát:

Most átcsoportosítunk, hogy úgy az egészek, mint a törtek egymás mellé kerüljenek:

Szintén gyakorlati szempontból írtuk a tört elé a — előjelet, tehát a tört nem


Itt kezdődik a tulajdonképpeni számítás. A diophantos egyenletek szellemében azt követeltük, hogy y egészszám legyen. Mivel x is csak egészszám lehet, 30—2x szintén az. De ha még y is egészszám, akkor a

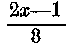


A fentiekkel azonos megfontolás szerint egyenletünket átalakíthatjuk olymódon, hogy n segélyével fejezze ki az x-et

Most az x-et, annak is egészszámnak kell lennie, a tört felbontásával ismét egész és tört részre oszthatom.

A meggondolás ismét ugyanaz, x és n1 szükségképpen egészszámok. Tehát



Ha a szintén egészszám n1-et n2-vel kifejezem, akkor az eredmény
2n2 = n1 + 1
vagyis
n1 = 2n2 - 1
Mivel most már valamennyi tört eltűnt, megoldottnak tekinthetem a feladatomat. Már csak egy, nem nehéz, de eléggé bonyodalmas feladatom van hátra. Vissza kell nyernem az x-et és az y-t, s kifejezésünkben csak a legutolsó n-et, esetünkben az n2-t hagyhatom meg. Minthogy n1 = 2 n2 — 1 és
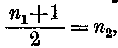

fejezése ez volt: 30—2x—
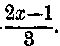

Mivel továbbá

Áttekintés céljából írjuk fel diophantosi egyenletünk úgynevezett végleges, általános megoldásait újból, egymás alá. Az n mellől az indexet már elhagyhatjuk, hisz az index megkülönböztetést szolgáló jelzés, tehát elveszti minden értelmét, ha már nincs megkülönböztetni való. n2 vagy n bárhogy is jelöljük most, tetszésszerinti egészszám, és
x=3n—1
y=33-8n
Lássuk, hogy az Euler-féle megoldás valóban helyes-e? n helyébe itt, mondtuk, bármely pozitív vagy negatív egészszámot (itt a nulla is egészszám) tehetünk. Az egyenlet:
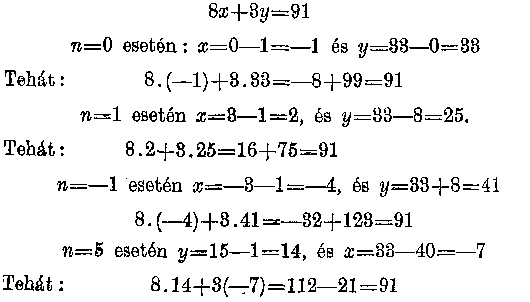
és így tovább, a végtelenségig, pozitív és negatív irányban.
Valóban, csodálatos ez az algoritmus, lehetővé teszi két ismeretlen végtelen sok egészszámú értékének egyszerű képlettel való rögzítését. Első, kitalált értékpárunk x—5 és y=17 az n=2 esetén keletkezik, mert ekkor x=6—1=5 és y=33—16=17.
Most további feltételeket is szabhatnánk és kereshetnék az 1 és 100, vagy a —10 és +10 közötti megoldásokat, vagy csak a pozitív, vagy csak a negatív értékeket. A gyakorlatban az ilyen megszorítások sokszor nagyon fontosak. A gyakorlott, vagy ügyes olvasó hamarosan rájön, miként lehet ilyen követelményeknek eleget tenni. Egyszerűen 0-tól felfelé és lefelé behelyettesítünk néhány számértéket, legjobb egy kis táblázatot felírni, és hamarosan kiderül, hogy meddig lehet elmenni. (Természetesen feltételi egyenlőtlenségeket is lehetne, teljesen korrekt módon, megadni. Pl. x>10, tehát (3n—1)<10, ezért 3n<11 és n < 11/3. Tehát az n legfeljebb 3 lehetne, hogy x 10-nél kisebb legyen. Most az y számára is fel kellene valamilyen egyenlőtlenséget írni stb.)
De a diophantosi egyenletek csak eszközei voltak célunknak, mint az a későbbiek folyamán kiderül. Nem mélyedünk tehát el érdekes különleges törvényeiben, csupán olyasmit jegyzünk még meg, amire már utaltunk. Azt ugyanis, hogy egyáltalán nem minden két ismeretlenes,
ax+by=c (a, b, c pozitív vagy negatív egészszám)
alakú egyenlet valódi diophantosi, vagyis nem minden egyenlet ismeretlenei számára található összetartozó, egészszámú megoldáspár. Egyenlet diophantosi jellegéhez még további feltétel teljesülése elengedhetetlen.
Tegyük először fel, hogy az egyenletünket, mint mondani szokás, legegyszerűbb alakra hoztuk. Ez azt jelenti, hogy addig osztottuk mindkét oldalát valamely közös osztóval, amíg ilyen csak volt, tehát további osztás lehetetlenné nem vált. Ha ez az egyenletünk
9x+12y=51
akkor 3-mal oszthatunk és
8x+4y=17
az egyenlet legegyszerűbb alakja.
Ha a
32x+24y=124
egyenletet a fenti módon 4-gyel egyszerűsítjük
8x+6y=81
adódik legegyszerűbb alakként.
Itt már habozunk. Megfejthetetlen, hogy miként lehet két páros szám összege páratlan? 8x és 6y pedig, ha x és y egész, feltétlenül páros. Mert 8∙5, 8∙7, 8∙(—2) és 6∙(—20), 6∙1 stb. minden körülmények közt páros.
Sőt azt is állítjuk hogy a
3x+15y=19
sem diophantosi. Mégpedig azért, mert nemcsak az együtthatók páros jellege játszik szerepet, hanem az a körülmény is, hogy van-e az x és y együtthatójának oly közös osztója, amellyel az állandó nem osztható.
Ezen állítás igazolását helyes, érvényes matematikai bizonyítás példájaként fogjuk felhasználni. De előbb lássunk még egy szemléltető példát.
9x+12y=51
hárommal osztva az eredmény
3x+4y=17
3 és 4-nek nincs közös osztója, egyenletünk tehát valóban diophantosi, egészszámokkal megoldható. Euler szerint a megoldás:

Itt nem alkalmaztunk indexet az n mellett az y—2 kifejezésben, mert a magában álló y-ról azonnal láttuk, hogy nem lesz több résztörttel dolgunk. n=3 esetén x=—9, y=11 és
8(—9)+4∙11=—27+44=17.
Ez esetben minden a legnagyobb rendben van, amint azt el is vártuk. De térjünk vissza a bizonyításhoz és az általános számokhoz. Tegyük fel, hogy egy egyenletet már a legegyszerűbb alakra hoztunk, vagyis az
ax+by=c
egyenletben a, b és c-nek már nincsen közős osztója, mert különben ez nem lehetne az egyenlet legegyszerűbb alakja. Az a-nak és b-nek még van közös osztója, de ezzel c már nem osztható. Hogy ez nincs kizárva, láthatjuk a következő példán is:
8x+6y=31
ahol 8 is, 6 is osztható még 2-vel. Általánosan azt mondhatjuk, hogy a és b közös osztója legyen m. Ez továbbá azt is jelenti, hogy a/m és b/m még egészszámok. Szorozzuk meg ezen egészszámokat a feltevésünk szerint szintén egészszámú x-szel és y-nal, az eredményt pedig adjuk össze.
Még egyszer: diophantosi egyenletnél alapfeltétel, hogy az ismeretlen együtthatóinak ne legyen az egyenlet legegyszerűbb alakjában közös osztója. De bármelyik ismeretlen együtthatójának és az állandónak lehet közös osztója, mint az a 3x+4y = 12 egyenletből is kiderül. (4-nek és 12-nek közös osztója a 4, 3-nak és 12-nek a 3.) Ezen egyenlet általános megoldása
x=4—4n és y=3n
tehát pl.
n=5-re x=4—20 = —16 és y=15.
A próba: 3(—16)+4∙15=-48+60=12.
TIZENÖTÖDIK FEJEZET
Nagyon csábító volna az egyenletek tanát tovább kutatni, mivel abban még egy egyenlettípusra akadnánk, amely megnyitja a voltaképpeni utat a felsőbb és legfelsőbb matematikához. Ez az egyenlettípus az úgynevezett «függvény», amely algebrai egyenletekből fesztelenül levezethető.
Kérjük azonban ezeket a szavakat mint egyelőre nagyon pontatlan célzást venni. A legközelebbi fejezetek már bevezetnek minket ebbe a bűvös világba. Mivel azonban a függvényekről szóló tanban sokkal szabadabban tudunk mozogni, ha előbb még van türelmünk a mi számfogalmunkat kibővíteni és a hatvány algoritmusát behatóbban tanulmányozni, azért nem sajnáljuk ettől a fáradságot.
Emlékezzünk vissza arra, hogy ugyanazon alapú hatványokat úgy osztunk, hogy a kisebbik hatvány kitevőt kivonjuk a nagyobbikből. Tehát például 105 : 103=105-3=102 vagy 100,000 : 1000 = 100. Vagy a17 : a6=a17-6=a11 stb. Itt hallgatólagosan azt a megállapodást tettük, hogy az osztandó hatvány mutatója mindig nagyobb vagy legfeljebb egyenlő volt az osztó hatványmutatójával. Tehát általánosan : az am: an osztásnál teljesül az m>n föltétel. Vagy ami ugyanaz volna : n<m. Mivel m-et és n-et mindig pozitívnak vettük, sohasem fenyegetett a veszedelem, hogy eredményül valamely alapot negatív hatványmutatóval kapjunk. Ámde magában véve egy negatív hatványmutató igen jól elgondolkodtató. A kérdés csak az, hogy mi értelme van a mi algoritmusainkon belül, anélkül, hogy felrobbantanánk a mi rendszerünket, amelyet eddig fölépítettünk.
Egyelőre még ragaszkodni akarunk ahhoz, hogy m és n pozitív számok, de ez alkalommal meg akarjuk fordítani a feltételi egyenlőtlenséget, azt állítva, hogy n nagyobb mint m (n>m vagy m<w). Mivel továbbá azt követeljük, hogy az n mutató az osztóhoz tartozzék, azért az am : an = am-n osztásnál okvetlen negatív számot kapunk az eredmény mutatójául, mivel a föltevés szerint nagyobbat kellett kivonnunk a kisebbikből. Konkrétabban kifejezve: a=10, m= 5, n=7; következőleg 105 : 107=105-7=10-2.
Konkrét számokkal fesztelenül számíthatunk. A mi kellemetlen eredményünket tehát egyszerűen kiszámítjuk. Például a következő módon:
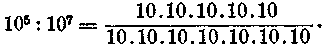
Mivel mármost nyilvánvalóan rövidíthetjük a felső öt tizes szorzót a nevező öt tizes szorzójával, azért mint eredményt a következőt kapjuk:
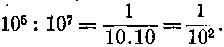
Már sejtjük az új algoritmust, de óvatosságból még egy próbát csinálunk.

És ez az
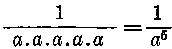
A mi keresett szabályunk tehát igen egyszerűen hangzik : valamely a alap negatív hatványmutatóval egyenlő ugyanazon alap fordított értéke ugyanazon pozitív hatványmutatóval. Mint képlet:

Az utolsó korlátozásnak megvan a maga helyes értelme. Mert ha a=0, akkor

Alig szükséges tovább egy szót is vesztegetni a negatív hatványmutatóról. Ami egyszerű szabályunk által ezt a hatványmutatót besoroztuk algoritmusaink közé és oly kifejezéseket, mint b(-3+2-4+6-8) = b-5 = 1/b5 éppen oly biztosan kezelünk, mint c(5+4-3) = c6
A fordított érték lényegéből folyik még, hogy 1/an előállítható, mint a°: an = a0-n = a-n.Ellenben úgy képzelhető, hogy így állott elő: a° : a-n=a0-(-n)=an. E szabály révén abban a helyzetben vagyunk, hogy bármely hatványt, ha tetszik, a hatványkitevő előjelének megváltoztatásával a törtszámlálóból a törtnevezőbe (és megfordítva) vihetünk át. Ezáltal adódik :

Most pedig még tovább akarjuk bővíteni algoritmusunkat. Ugyanis állítjuk, hogy lehetőnek kell lenni a hatványmutatót közönséges törtek alakjában írni. Tehát például: 105/6, a7/8, 15a/b, 201/10, 43/7, 925/8, stb.
Az rögtön világos, hogy egyelőre semmit sem tudunk elképzelni valamely tört, mint hatványmutató gyanánt. Mert az a követelés, hogy vegyem a 10 alapot például 5/6-szor mint tényezőt: az első pillanatra értelmetlen kívánságnak látszik. Még akkor is, ha akként akarok magamon segíteni, hogy az 5/6-ot szétbontom 5*(1/6)-ba, csak azt tudom, hogy először
a 10-et 5-ik hatványra szabad emelnem, mivel (105)1/6 is egyenlő 105/6-val. Az 5-ik hatvány tovább nem okoz nehéz-
séget. De hogy emelem 1/6 hatványra a 105=100,000 eredményt? Miként vehetem a 100,000-et egyhatodszor mint tényezőt? Nagyobb ezáltal aligha lesz, mivel még egyetlen egyszer sem kell tényezőül vennem. Itt tehát minden jel szerint egy új leépítő, litikus számolási mód előtt állok, amely úgy viszonylik a hatványozáshoz, mint az osztás a szorzáshoz vagy mint a kivonás az összeadáshoz.
El akarjuk árulni, hogy miféle új számolási módról, miféle «parancsról» van szó: az úgynevezett gyökvonásról vagy gyökfejtésről. És (100,000)1/6 mint «parancs» nem jelent mást, mint a következőt: «keress egy még ismeretlen számot, amely hatszor tényezőül véve értékül 100.000-et ad».
Ha általánosan ca/b állott volna előttünk, írhattuk volna: ca/b = (ca)1/b, ami annyit jelent, minthogy keresni kell egy még ismeretlen d számot, amely b-szer tényezőül véve, újra ca-t ad. Tehát (d*d*d*d*d ....) b-szer, mint tényező = ca vagy
db = ca.
Ámde gyököket — amit mindenki tudhat — nemcsak fordított értékű hatványmutatók alakjában — tehát pl. a1/2, b1/3, 101/b, stb,—írnak, hanem sok század óta alkalmazzák a gyökjelt, ami a radix (gyökér) szóból akként állott elő, hogy széthúzták



Itt a gyöknek úgynevezett gyökmutatója vagy gyökkitevője van, ami nem más, mint a fordított értéke a törtnek, amelyet mint hatványmutatót már ismerünk. Tehát:

Tárgyalásunkból könnyen adódnak a gyökök kezelésének összes szabályai. És ajánljuk biztonság kedvéért a gyökökkel való összes bonyolultabb számítást utánavizsgálni, törtkitevőkkel való számítással, vagyis változtatva az algoritmust;

Ha a gyöknek tört a mutatója, akkor hatványként való írásánál a fordított érték veendő. Például
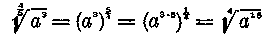
vagy
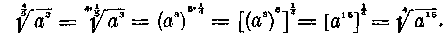
Természetesen lehetséges osztani is gyökökkel (tört kitevőjű hatványokkal), amikor is pozitív vagy negatív eredmények adódhatnak. Például

Végül megjegyezzük, hogy a második gyököt rendesen nem írjuk ki, azaz hogy



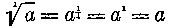
Azt mondtuk «végül». A gyökökről szóló tanításunkat szándékosan csak nagyon felületesen végeztük. Mivel a mi további céljainkat tekintve, nem oly dolgok érdekelnek, amelyek minden tankönyvben pontosan és részletesen megvannak, hanem egy hasonlíthatatlanul mélyebb probléma érdekel. T. i. a számfogalom belső lényege és e fogalom bővítése a gyökművelet, a gyökvonó parancs bevezetésével, amelyet — mellékesen megjegyezve — egyszerűbb módon, az ú. n. logaritmusok segítsége nélkül számszerűleg tényleg véghezvinni csak bizonyos és nagyon korlátolt esetekben lehet. (Elvben minden gyök valamely konkrét számból kiszámítható. Az e célra kieszelt eljárás azonban, mint említettük, nagy gondot és fáradságot kíván, úgyhogy a számító praxisában alig jön tekintetbe.)
TIZENHATODIK FEJEZET
Irracionális számok
Ha fölvetjük a kérdést, hogy mely föltétel alatt számítható ki, egész általánosan véve, valamely gyök, azt találjuk, hogy például


Tehát p az eredmény és azt mondjuk, hogy p az a "negyedik gyöke".
Utána kell azonban néznünk, hogy vajon ez a lehetőség mindig adott-e. Vegyük a legegyszerűbb esetet és követeljük, hogy a egész szám legyen. Valamely tetszőleges egész szám. Ha ebben már megállapodtunk, azonnal észrevesszük, hogy nagy véletlen szükséges ahhoz, hogy a valóban egy más p egész szám negyedik hatványa legyen. Mert az első száz pozitív egész szám között például negyedik hatványként csak a következőket találjuk : 1, 16 és 81. Azaz, bármely egész a esetén — kivéve az 1, 16 vagy 81 értékeket — nincs pozitív egész szám, amelynek negyedik hatványa a. A 25 például a 24 és 34, a 90 a 34 és 44 között van, stb. A matematikában az «egyenlőtlenségeket» alkalmazzuk ennek a "közöttiségnek" a kifejezésére. Mivel egy rendkívül fontos írásmódról van szó, amelyet különösen a felsőbb matematikában állandóan alkalmaznak, azért erről részletesebben akarunk szólni. Ha például följegyezni akarom, vagy föltételül állítani, hogy a b szám 30 és 40 között van, akkor írom:
30 < b < 40.
Ha ellenben azt akarom mondani, hogy b esetleg maga a 30 vagy 40 is lehet, akkor írom:
30 ≤ b ≤ 40.
Ezt az eljárást "határok közé zárásnak" is nevezik és itt 30 az alsó, 40 a felső határt jelenti. Általános számoknál természetesen nem tudom előre, hogy melyik szám a magasabb vagy a mélyebb. Ha írom, hogy
a < b < c,
akkor b van az a és c között. És e tétel révén, közvetve, tudom csak meg, hogy a három szám közül a a legkisebb, c a legnagyobb. (Az, hogy mikor a<b és b<c, akkor egyúttal a<c, ez egyik esete az úgynevezett tranzitivitás elvének.)
Avégre, hogy ebből az írásmódból hasznot húzzunk mi gyökeinkre nézve, mondhatjuk 25 a 24 és a 34 között van,
24 < 25 < 34.
Nyilvánvaló tehát, hogy a 25 negyedik gyöke nem számítható ki
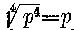
Van azonban nekünk egy másik fajtája is a számoknak, amelyek végtelen sokaságban és fokozatban vannak az egész számok között. Ezek a közönséges törtek. Mondtuk már, hogy például a törzstörtek 1/2, 1/3, 1/4, 1/5, és így tovább,

a 0 és 1 között vannak, valamint még az összes többi valódi törtek, mint 2/3, 3/4, 4/5, 5/6, 6/7, ...(∞-1)/∞ -ig. (Egyszerűségért ∞-t írunk «végtelen határértékhez közeledő nagy szám» helyett.) Mivel azonban tetszőleges más egész számok között is középértékek helyezendők be — pl. 12 és 13 között nem valódi tört, tehát 25/2 = 12 1/2 vagy 12 + 1/2, 12+3/4, 12+7/8 stb. alakjában — azért jogosult remény, hogy a mi

A kipróbálás nagy fáradságot okozna és talán még afelől se biztosítana, hogy ezt a törtet valóban megtaláljuk. Ugyanis — ezt még egyszer hangsúlyozzuk — végtelen sok tört között választhatunk, amelyek nevezője 200 vagy 2000 vagy 2,000,000 jegyből is állhat. Talán a


pontos értékét csak egy oly tört révén találnánk meg, amelynek nevezője 10.000 kvintillió jegyből áll, vagy ez a szám még megszorozva egy billió szextillióval. Még mindig egy közönséges tört volna. És a nevező jegyeinek száma még mindig tovább és tovább emelhető. Problémánkat tehát általánosan kell vermünk, ami nem nehéz. Tudjuk, hogy két eset van. n-ik gyöknél ez az a egyenlő lehet pn-nel, ahol a és p pozitív egész számok. Vagy pedig a mi a-nk két egymás után következő szám, p és (p+1) n-ik hatványa között van. Tehát pn<a< (p+1)n. A (p+1) a p-re következő legközelebbi egész szám, mint például 17-re a (17+1)=18 szám következik. Mivel továbbá tudjuk, hogy a második esetben gyökn(a) számára egész számot nem kaphatunk, azért azt kérdezzük, hogy vajon nem fejezhető-e ki valamely — közönséges törttel. Ekkor gyökn(a) egyenlő tartoznék lenni
nel, mivel ekkor is egyenlő volna (r/s)1 = r/s - sel és így a gyök ki lenne számítva, mint közönséges tört. Magától értetődik, hogy r és s "közös osztó nélküliek", mivel a törtet a legegyszerűbb alakra hoztuk.
Például nem 24/15-öt, hanem 8/5-öt írnánk fel megoldásul.
Mivel
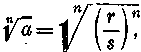
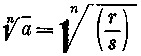
hogy

És r és s közös osztó nélküliek. De ha számláló és nevező közös osztó nélküli, akkor oly sokáig hatványozhatom, ameddig akarom és ekkor sohasem lesz közös mértékük, mivel azáltal új tényező nem lép föl sem a számlálóban, sem a nevezőben. Ha például 3/5-öt hatványozom, akkor kapom

Így hát közösosztó nélküli számok n-ik (tetszőleges) hatványai is egymásra nézve közös osztó nélküliek maradnak. És közös osztó nélküli számok egymásai osztva sohasem adhatnak egész számot, tehát a mi a-nk soha sem lehet (r/s)n, ameddig fenntartjuk az a egész számúságának a feltételét.
A mi eredményünk egyenesen megijeszt. Mivel nem kevesebbet mond, mint azt, hogy habár az egész számok között levő törtek sokasága végtelen, mégsem tudok közönséges törtet találni, amely lehetővé teszi például a


A mi eredményünk — mint a görögök Pythagoras óta mondták — «alogos», kimondhatatlan, értelem nélküli.
Ellentmond az értelemnek, a "ració"-nak. (Az irracionálisnak a rációból való levezetése a "helyes viszony" értelmében, az inkommenzurábilis fogalmánál fog megtörténni.) És ezeket az új, misztikus számokat, amelyekről még azt sem tudjuk, hogy miként írandók, «irracionális», nem-racionális számoknak nevezzük.
De hogyan fejezzem ki ezeket a kifejezhetetlen számmonstrumokat, ezeket a különös közbeeső számokat, ha tilos úgy törtként, mint egész számként való írásuk?
Például


Azaz π/4 csak akkor volna kifejezve, ha ebben a sorban a végtelenségig számoltam volna. Tehát tetszőleges pontosan tudok számolni, de sohasem végig.
Már most két lehetőséget látunk irracionális számok kifejezésére, amelyek valójában ugyanoda lyukadnak ki. Tudniillik a tizedestörtek alakjában való írást és a végtelen sorok alakjában való írást, amely utóbbiak — mint a «Leibniz-sor» mutatja — keverhetik is az összeadást és a kivonást, amikor «alternáló» soroknak nevezik őket.
De még nem akarunk közelebbről foglalkozni a végtelen sorok nagyon nehéz tanával hanem ezt csak annyira akarjuk átkutatni, amennyire annak az állításunknak az igazolására szükséges, hogy az irracionális számok mindkét írásmódja voltaképp ugyanazon az elven nyugszik: t. i. éppen a végtelen sorokkal való előállításon.
A Leibniz-sor megvizsgálhatósága végett már most megemlítjük, hogy a π körszám értéke tizedesen írva 3,141592653589798... Egy másik ismert irracionális szám volna például a természetes logaritmusok alapja, az ú. n. "e szám", amely mint sor

és mint tizedesszám
e = 2,71828182845904523586... alakban fejezhető ki.
Ámde most ellenfelünk joggal figyelmeztet, hogy mi tizedestörtekről még egyáltalán nem beszéltünk, tehát ha nem tételezünk fel semmilyen előzetes tudást, akkor nincs jogunk tizedestörteket felírni. Továbbá tehetségesebb és figyelmesebb olvasók azonnal közbevetik, hogy hát elég oly eset is adódik, amelyekben egy közönséges osztás — amint mondják — nem «megy fel». Itt valami nincs rendjén. Ugyanis tetszőleges egész számok osztása nem más, mint parancsként felírt közönséges tört vízszintesen felírva a kettőspont alkalmazásával. És azt állítottuk, hogy a közönséges törtek és irracionális számok egymással merőben ellentétesek; és hogy az irracionális számok a legközelebb szomszédos közönséges törtek (vagy osztások) «között» fekszenek. Továbbá mi úgy tettünk, mintha az irracionális számok csak a gyökvonás litikus műveletével állottak volna elő, holott ismeretes, hogy például 20 : 6 vagy 20/6 éppenúgy irracionális számot, tudniillik a 3,33333338... vagy 3,3. (három periodikusan) vagy
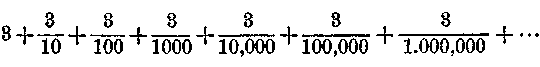
számot szolgáltatja.
Nagyon hálásak vagyunk ezekért az ellenvetésekért. Mert feltűnő jelenség, hogy még jó számolók és gimnáziumi képzettségű emberek sem igazodnak el ezekben a különbségekben, sőt még nem is gondolkodtak erről vagy nem is ismerik ezeket kellőképpen.
Hogy valamely tört különbözik egy irracionális számtól, ezt mindenki belátja. Ugyanis a közönséges tört lezárt, kész, bevégzett; ellenben az irracionális szám sohasem állítható elő mint szám, hanem mindig csak mint végtelen, soha le nem záródó processzus, mint számolási szabály, mint képzési törvény, mint sor. Nevezhető volna ezért az egész és a törtszám sztatikái számnak, az irracionális szám, az írásnak megfelelően, dinamikus számnak. Nem mennyiség, hanem egy irány bizonyos mennyiséghez, jóllehet mi mindig, részben megcáfolhatatlanul sztatikaivá tehetjük. És ezt megtehetjük, amennyire akarjuk. Ha



található meg a számegyenesen. Még akkor sem, ha tudnám, hogy mely közönséges törtek között fekszik. Mert valahol ott van más irracionális számok egy végtelen sokaságában. Ez nagyon misztikusnak tűnik fel. Sajnos azonban a mi kereteink között nincs meg a lehetőség ezt a rendkívül felizgató dolgot maradéktalanul tisztázni.
TIZENHETEDIK FEJEZET