Közönséges törtek
Még egy kis dombocskán kell túljutnunk, hogy azután szabadon mozoghassunk a matematikai rejtvények síkságán. Az osztásnak különleges írásmódjáról van szó, amely elvi újítás jellegű algoritmusunkban.
Történeti sorrendben a kettőspont jelent meg legutoljára az osztás jeleként. Eddig mi úgyszólván kizárólag ezt használtuk az osztás jelölésére. Ezt a jelet is Leibniz szerencsés keze teremtette. A törtvonal, mint az osztás jele sokkal régebbi eredetű.
Tört egyelőre nem jelent egyebet, mint véghez nem vitt, vagy egészszámú eredménnyel keresztül nem vihető osztást.
Ezúttal kivételesen általános számokon kezdjük, mert azoknak nagysága, nagyságuk viszonya semmiképpen sincsen meghatározva, így a tört típusaként felírhatjuk az a/b kifejezést. Ennek a jelentése a törve b-vel, a per b, a osztva b-vel, a:b, vagy a viszonylik b-hez. A törtvonal feletti szám a számláló, az alatta levő a nevező. Ha számláló 1, tehát általánosan 1/a, 1/b, 1/c stb., akkor egységtörtről beszélünk. Ha a számláló kisebb mint a nevező, akkor valódi törttel van dolgunk; általánosan ezt úgy lehetne írni, hogy
a/b valódi tört, ha a<b. (Ha a és b pozitív számokat jelentenek.) Az ez alkalommal először előforduló egyenlőtlenségi jel (>, <) hegye mindenkor a kisebb szám felé fordul, nyílása pedig a nagyobb felé. Természetesen visszafelé is lehet olvasni, jobbról balra, s egyformán jogos kijelentés az (5+7—2) > (1+3—2+1) kifejezés kiszámítása után az, hogy 10 nagyobb mint 3 és az, hogy 3 kisebb mint 10.
De visszatérve törtjeinkhez, akkor mondják az törtet valódinak, ha pozitív a és b esetén a<b. És akkor nemvalódi vagy áltörtnek, ha a>b. Konkrét számokhoz visszatérve 1/3 egységtört és egyúttal valódi tört is, 2/3 valódi tört. 6/4 vagy 3/2 áltörtek, mert egészszámok és törtek összegeként is írhatók. Értékük ugyanis 1 + 2/4 vagyis 1 + 1/2.

A régi egyiptomiak és görögök számításaiban az egységtörteknek nagy szerep jutott, helyett az egyiptomiak az
egységtörteket írták és Görögországban is mindennaposak voltak a hasonló felbontások. Ma már el szoktuk hanyagolni az egységtörtekre bontást, minthogy mindennemű törttel könnyen és biztosan tudunk bánni. Csupán az integrálszámításban játszik még némiképpen hasonló eljárás szerepet, az úgynevezett részlettörtekre való bontás.
De a tört fogalma másra is megtanít minket. Rajta szerezzük első tapasztalatainkat gy szám részeiről. 1/3 az egységnek a harmada, 5/7 ötnek a hetede. Itt tehát valami olyan mutatkozik, mégpedig a valódi törteknél, ami a felosztás fogalmán túlmegy. Itt már nem az a kérdés, hogy valamely egész számot mily egészszámokra tudom felosztani, mint 12: 3 = 4 esetén például, amikor négyszer háromból keletkezettnek tekintem a tizenkettőt, vagy ahol a 12-ből a 3 által lesz a 4; hanem most az a feladat, hogy milyen közbenső számokat találhatok az egészszámok között, egészszámok osztása segítségével. 1/3, 2/3, 3/4, 5/7, 29/38 értéke egyaránt 0 es 1 közé esik. És végtelen sok ilyen számot tudunk felírni, amelyek mind 0 és 1 közé esnek, csupán a számlálót kell mindenkor kisebbnek választanunk a nevezőnél. Ezek szerint valamennyi valódi tört 0 és 1 közé esik. Értékük változatlan számláló esetén annál kisebb, minél nagyobb a nevezőjük.
2/25 nagyobb, mint 2/729, s ez mindenkinek világos, akinek csak
valami fogalma van a részekre bontás lényegéről. Ha a számláló és a nevező azonos, akkor az egység más írásmódjáról van szó. Mert a/a ugyanannyi mint a : a, ez utóbbi pedig mindenkor eggyel egyenlő. Ha a számláló 0 akkor a tört értéke természetesen szintén 0. Ha viszont a nevező 0, akkor a legnagyobb zavarban vagyunk. Valamit semmivel kellene osztanunk. Tehát a: 0=? Ha a megoldás próbáját akarjuk megcsinálni, akkor olyan számot kell keresnünk, amely 0-val szorozva a-t ad. Szemmel látható, hogy lehetetlen a kívánság, mert bármely, mégoly nagy szám is, nullával szorozva nullát ad. De ha másképpen számolunk, (majdnem azt mondanám, hogy nem «sztatikusan», hanem (dinamikusam), akkor következőképpen okoskodhatunk : 5 osztva 100-zal 5 századot ad eredményül. 5 osztva 47-tel már sokkal több. Többet kapunk, ha az osztó 21, még többet, ha 7, annál is többet, ha 5, ez utóbbinál 1 az eredmény. Ha 3-mal osztunk, az eredmény 5/3, azaz 1 1/3, ha 2-vel osztunk, az eredmény 5/2 vagyis 2 1/2, végül 1 esetén a hányados 5. Ha most sorban valamennyi 1 és 0 közt fekvő számmal osztanánk, tehát valamennyi valódi törttel, például 5 : 1/20, 5 : 1/365, akkor nagyon gyorsan növekedő értékeket kapnánk. Mert 5 : 1/20 már 100, 5 : 1/365 pedig 1825, 5 : 1/100,000 pedig már 500,000 és így tovább. A nulla maga kisebb minden törtnél, ha annak még oly nagy is a nevezője.
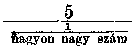
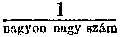
még mindig nagyobb nullánál. Tehát nagyobb minden elképzelhető nagy számnál.
S még annál is nagyobb. Erre a folyamatra kell gondolni, amikor azt mondjuk röviden, hogy 5/0 végtelennel egyenlő. Jelekkel 5/0 = ∞. Mindaz, amit mi itten csak olyan felületesen számolgattunk, tulajdonképpen már a végtelen analízishez tartozik és határérték-megállapítás, «limes-megállapítás» a neve. Nem állíthatom ugyanis, hogy 5/0 egyenlő végtelennel, csupán azt, hogy a végtelenbe növekszik. Azt, hogy oly határhoz (latinul limes=határ) közeledik, amelyet végül is csak a végtelen fejez ki tekintve, hogy a nagy, nagyobb, legnagyobb, legeslegnagyobb, sokszorosan legeslegnagyobb fokozást tetszés szerint folytathatom, de a képzés törvénye, a növekedés változatlanul fennmarad.
Szándékosan nyújtunk megfelelő helyen kilátást végcélunkra, ha mégúgy óv is ettől ellenfelünk. Mert azt hisszük, hogy az "alsóbb matematika" éppen attól nyeri kellemetlen, szakadozott, meg nem nyugtató jellegét, hogy ilyen helyzetben rendszerint dogmákra utal, vagy kerülgeti a dolgokat, mint a macska a forró kását. Mi nem kerülgetjük, hanem nyíltan kimondjuk: azon állítás, hogy a:0 = ∞ lehetetlenség, mert ∞ x 0 mindaddig csak nullát adhat eredményül, amíg a dolognak tisztán a sztatikus oldalát tekintjük. De mihelyst a nullát közelítéssel nyert minden képzelhetőnél kisebb számnak, valamely folyamat határértékének tekintjük, a végtelent pedig valamilyen ködös óriásszámnak és szintén határértéknek, akkor algoritmusunk sérelme nélkül írhatjuk, ha rövidítve is, hogy a:0=∞. Hasonló különleges dologgal már eltűnő négyszögünk esetében is találkoztunk, sőt ottan 0 : 0 értékének meghatározása volt a feladatunk.
De kitérésünk még egy különleges eredményhez vezet. Mivel minden, tetszésszerinti szám (esetünkben az 5, hisz azt vaktában választottuk) az előbbiek szerint nullával osztva végtelent ad eredményül, a művelet próbájának is sikerülnie kell. Ezek szerint: 5:0 = ∞, tehát 0 x ∞ = 5; ugyanez igaz azonban 7 : 0 vagy 530 : 0 esetére is, vagy bármely véges a szám esetére is. Így tehát 0 x ∞ bármely véges számot jelenthet. Ez az első eset, hogy valamely számítási műveletünk eredménye határozatlan.
De már most vétkesen nagy távolságra csavarogtunk el "törtjeinktől". S még messzebb kell elmennünk, mivel az imént azt a szót ejtettük ki, hogy «arány» (más szóval viszony). Milyen mellékértelmét jelenti az osztásnak, ha azt mondom, hogy «a aránylik a b-hez» és ezt úgy írom, hogy a : b vagy a/b? Legegyszerűbben akkor fogjuk a dolgot megérteni, ha feladatunknak valamilyen mérési, geometriai értelmet adunk. Megmérjük egy derékszögű négyszögalakú asztallap méreteit és hosszát 6 méternek, szélességét 2 méternek találjuk. Minden gyerek azonnal rámondja, hogy a hosszúság úgy aránylik a szélességhez, mint 6 a 2-höz. Vagyis 6 : 2=8, tehát az asztal 8-szor olyan hosszú mint széles. Az úgynevezett aránynál tehát az egyik összehasonlítandó (arányba állítandó) mennyiséget a másik mértékegységnek választom, mert azt is mondhattam volna, hogy a szélesség úgy aránylik a hosszúsághoz, mint 2:6 vagy 2/6 azaz 1/3, vagypedig hogy az asztal egyharmad olyan széles mint hosszú. Valaminek a mértékét meghatározni nem más mint megmondani, hogy hányszor van meg az egység az egészben. De ez ismét nem egyéb, mint az egységgel történő osztás. Első esetben a szélesség volt az egység. A hosszúság három egységet tartalmazott. A második esetben a hosszúság volt az egység és a szélesség egyharmad egységnyi volt. De ha az egység keresését elhalasztjuk és valamilyen külső egységet vonunk be, például a métert, azt mondhatjuk, hogy a hosszúság úgy aránylik a szélességhez, mint 6 méter a 2 méterhez. Teljesen általánosan; a hosszúság a szélességhez, mint a : b, vagy a/b valamilyen egységben kifejezve.
Ezt az egyenlőségi jellel azonosnak kívánt két arányt, aránypárnak, vagy aránylatnak hívják. Ilyen pl.
a : b=6 : 3 vagy
27: 9 = 15 : 5 másképp 27/9 = 15/5.
De mivel az aránylat nem egyéb mint egy kötött formájú egyenlet, megelégszünk eddigi utalásainkkal és részletes vizsgálatainkat az egyenletek tárgyalásánál fogjuk megejteni.
Most azonban már igazán vissza kell térnünk törtjeinkhez és a rájuk vonatkozó számítási szabályainkat, algoritmusunkat kell megvizsgálnunk.
Első az összeadás és a kivonás. A törtek, mellékesen már megállapítottuk, új, az egészszámok közé eső számok. A valódi törtek nagyságra a 0 és az 1 közt vannak, az áltörtek valahol másutt a számsorban. Természetesen a törteknek is van előjelük. Vagyis léteznek negatív törtek is.
Ha a közönséges törteket (A közönséges és tizedes törtek szétválasztásával később fogunk foglalkozni.) tekintet nélkül arra, hogy valódi törtek-e vagy pedig áltörtek, új számoknak tekintjük, akkor számunkra ugyanazt a szerepet játszhatják mint az alma vagy a körte stb. Alma jelentse az egyharmadot, körte az egynegyedet, a citrom pedig az egyhetedet. A tört jellegét kizárólag a nevezője határozza meg. A tört nevét adja. 3/4 az háromszor 1/4. Tehát a számláló együttható jellegű és 1/4 azt jelentheti, hogy 3 x 1/4 , vagyis három darab új, törtet jelentő körte. Ez egyszerű megfontolásból a törtek összeadásának és kivonásának algoritmusa azonnal következik. Csak egynevű törtek adhatók össze és vonhatók ki egymásból. Tehát összevonhatjuk, összeolvaszthatjuk, közös nevezővel írhatjuk őket, következőképpen

De ha a nevezők különbözők, akkor az új, közös nevezőt előbb meg kell keresnünk. Azt, hogy ez miként történik, azt hiszem, teljes joggal tekinthetem ismertnek, s csak egy példát kell felhoznom a legkisebb közös többszörösre.


Itt a közös nevez 3∙5∙8∙13, tehát 1560. Ahhoz, hogy valamennyi törtet 1560-ad részekké tegyem, természetesen a számlálókat is meg kell változtatnom, nehogy az egyes törtek értéke megváltozzék. 1/3 1560-adokban 520/1560, s rövidítéssel meg is győződhetek erről. A gyakorlat azt a kérdést veti fel, hogy mivel kell a számlálót megszoroznom, hogy ugyanazt a törtet más nevezővel kapjam meg. Minthogy 1560 annyi mint 3∙5∙8∙18, tehát 1/3 annyi mint
és így tovább. Számításunk eredménye tehát a következő

Általánosan valamely összeadás vagy kivonás ilyen volna:

Azt hiszem fenti általános eset gondos tanulmányozása után a törtek összeadásának és kivonásának, valamint a közös nevező megtalálásának módja teljesen világos lett. Ha a közös nevező valamennyi nevező szorzata, akkor minden számlálót a többi tört nevezőjével kell megszoroznom, hogy egyforma nevezőjű, de változatlan értékű törteket kapjak.
De mivel a törteket úgy tekintettük, mintha névadó egységtörtből (1 törve a nevezővel) és együtthatóból (számláló).
állnának, azonnal megkaphatjuk a szorzás egyik szabályát. Törtet úgy szorozhatok, hogy a számlálóját (az együtthatót) szorzom. Háromszor egy heted egyenlő 3x(1/7) = 3/7. Vagy 6-szor 4/29 = 6x4x(1/29) = 24/29. Általánosan a∙b/c = ab/c. De mivel a tört nem csak a számláló növekedtével lesz nagyobb, hanem akkor is, ha a nevezőjét csökkentem, más módon is szorozhatok. Kétszer egy negyed egyszer egy féllel is azonos. Vagyis 2 • (1/4) = 1/(4/2) = 1/2, de ezt természetesen 2/4 = 1/2 számításmóddal is megkaphattam volna. Általában a(b/c) = b/c:a. Ez utóbbi szabályt használjuk a «rövidítéshez». Például 9(5/27) így is írható 9x(5/3x9) = 5/(3x9:9) eredmény 5/3. Ez ugyanaz, mintha (9x5)/(9x3)-et 9-cel rövidítettem volna.
Ha törtet törttel kell szoroznom, akkor valamennyi számlálót és valamennyi nevezőt összeszorzom. Pl.:

vagy konkrét számokkal
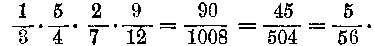
A legutolsó példánál már előre «rövidíthettem» volna. Minden számlálót és bármelyik nevezőt szabad ugyanis együtt rövidíteni, hisz valamennyi számláló az eredményben tényezőként szolgáltatja az új számlálót és valamennyi nevező az új nevezőt. De ezt is joggal gondolhatom ismertnek, hisz az elemi számolni tudáshoz tartozik.
Most már csak a törtek osztása és hatványozása volna hátra. Vegyük a hatványozást előre, mert az a szorzásnak csak egy módosulata.

A szabály tehát igen egyszerű és azt mondja, hogy a számlálót és a nevezőt egyaránt ugyanarra a kitevőre kell hatványoznom.
Ha törtet kell osztani, akkor semmiféle új szabályra sincs szükségünk. Minthogy a számláló az n-ed részek számát adja meg, egyszerűen a számlálót osztjuk, 3/4 : 3 természetesen 1/4 ugyanúgy mint három alma osztva hárommal egy almát ad. Bonyolultabb a kérdés, ha törtet, vagy egy egész számot kell törttel osztanunk. 5 : 3/4 nem képzelhető el azonnal. Csupán az bizonyos, hogy az eredmény nagyobb mint 5, mert 3/4 kisebb mint 1. De mekkora az eredmény?
A régi egyiptomiak és görögök módjára az egységtörtekhez menekülünk. Igaz, kissé más módon. Következőképpen okoskodunk : ha 30 osztandó 15-tel, akkor nyugodtan írhatom helyette, hogy 30 : (5x3), mert ez ugyanaz. Rajtam áll a választás, hogy először 5-tel osztok, s azután az eredményül adódó 6-ot 3-mal és így kapom a helyes, 2, eredményt. Oszthatnám először a 30-at 3-mal és azután a 10-et 5-tel, az eredmény, 2, ugyanaz. Így járunk el a törttel is. Mivel 5 osztandó 3/4-del, így írjuk 5:(3 1/4). Osszunk először 1/4 -del. Ez utóbbi az egységben négyszer foglaltatik, 5 egységben tehát 20-szor. A húszat mostan tovább kell osztanom hárommal, az eredmény 20/3 másképp 6 2/3. Lássunk egy másik példát. 7 : 5 = 7 : 1/9 A tört a 7 egységben 63-szor van meg, 63 tovább osztandó 5-tel. Az eredmény 63/5 azaz 12 3/5. Ha közelebbről megnézzük az eljárást, felfedezhetjük, hogy az egységtört nevezőjével meg kell szorozni az osztandót, s azután a számlálóval, amely mint második tényező szintén ott van a zárójelben, el kell osztani az eredményt. Általában:
Osztandó : számláló / nevező = osztandó : (számláló x 1/nevező) =
= (osztandó x nevező) : számláló.
De a legutóbbi eredményt ilymódon is írhatnám: