osztandó: számláló/nevező = osztandó x nevező/számláló, mivel az előbbi végeredményt is írhattam volna (osztandó x nevező) / számláló alakban.

Ezzel eljutottunk a «reciprok érték» fogalmához. A reciprok értéket akkor kapjuk, ha a számlálót és a nevezőt felcseréljük. 3/4 reciprok értéke 4/3, 5/9 reciprok értéke 9/5 és általánosan a/b -nek b/a. S mivel mindeddig csupán csak az «osztandóról» beszéltünk, de egyáltalán nem mondtuk, hogy annak egészszámnak kell lennie (annál is kevésbé, hisz az osztással kapcsolatos minden művelet az osztóban játszódik le), most teljesen általánosan megállapíthatjuk, hogy valamely számot törttel úgy osztunk, hogy a tört reciprok értélével megszorozzuk. Tehát n: a/b = n • b/a, ahol az n általános

vagy konkrét, pozitív vagy negatív, egész- vagy törtszám egyaránt lehet. így tehát

Kíséreljük meg új szabályunk szerint kiszámítani első példánk eredményét.

Algoritmusunk tehát hibátlan. Sőt ezen kívül a józan ész is igazolhatja. Igaz, hogy ez az igazolás teljesen csak a legegyszerűbb esetekben tekinthető át. Ha ugyanis valamely számot 1/2 -el osztok, világos, hogy az eredmény csak az osztandó kétszerese lehet. 2-szer, vagyis 2/1-szer az osztandó,

minthogy bármely egészszámot olyan törtnek írhatok, amelynek a nevezője 1. Futólag számítsunk ki még néhány példát:

Megfontolásaink a dupla-, emeletestört fogalmához vezettek, de ez nem egyéb mint más írásmódja törtnek törttel való osztásának.

Az utóbbi eset azt is megmutatta nekünk, hogy miként kell törtet egészszámmal osztani. Mégpedig a törtnek tekintett egészszám reciprok értékével való szorzással. Tehát:

Ebből az eredményből ismét új számítási szabály következik. Minthogy két egészszám osztását mindenkor fel tudjuk törtek osztásaként írni, például így: 

Láthatjuk, hogy egészszámok osztása helyett is bármikor az osztó reciprok értékével való szorzást tehetjük. Így :

Ez algoritmus sokszor nyer alkalmazást a gyakorlati számolásban és a számológépek szerkesztésénél és kezelésénél.

Most már elvi megvilágításhoz elegendő mértékben megismertük a közönséges törtek kezelését, tekintve, hogy nem a számolásban történő teljes kiképzés a célunk, s így hozzáfoghatunk a régen ígért «egyenletek» tanulmányozásához.

TIZENHARMADIK FEJEZET

Egyenletek

Utaltunk már arra. hogy az "ismeretlen x» az egyenletekről szóló tanban játszik nagy szerepet. Továbbá állítottuk, hogy az egyenlet algoritmus, s olyan, mint mindenféle rejtvények megoldását szolgáló, finoman kieszelt gondolkodó- és számológép. Végül még megállapítottuk, hogy az egyenlőségi jel nem puszta megállapítást nyújt, hanem parancs. Parancs, amely szerint x értékét úgy kell választanunk, hogy, amint mondani szokták, az egyenletet kielégítse, az egyenlőség valóban fennálljon.

Mindennemű elméleti megfontolás nélkül adjunk fel magunknak egy rejtvényt. Kérdezzük tehát: "mekkora az az x szám, az az előttem teljesen ismeretlen szám, amely a következő feltételeknek megfelel: megszorzom először 7-tel, hozzáadok 19-et, elveszek belőle 4-et és így az eredeti x-et, 10-zel megszorozva kapom eredményük). Matematikai módon írva:

7x+19—4=10x

Természetesen kiszámíthatom először mindazt, ami kiszámítható. Ezt kapom:

7x+15=10x

Akkor elkezdhetném a számokat, 1-től kezdve sorban x helyébe tenni, kipróbálni, és x=5 esetén, a következőképpen egyenlőséget kapnánk.

35+15=50

A rejtvényt megoldottuk tehát. x=5. De az eljárás minden inkább mint kielégítő. Először nem tudhatom előre, vajon az x szám egész-e vagy pedig tört. Azt sem tudom továbbá, pozitív-e, vagy negatív. Végül még azt sem tudom, nem létezik-e az ötön kívül még számtalan más megoldás is.

De még mielőtt hozzáfogunk egyenleteink algoritmusának tanulmányozásához, szemléljük meg közelebbről magát a szót és az egyenletek lényegét. Bocsánat a kuruzslásért. De az "egyenlet" szó nem is az igazi, jellemző kifejezése annak ami itt történik. A latin «aequatio» sokkal megfelelőbb volt. Latinul az igékből a -tio képzővel alkotott szavak működést jelentenek. «Aequatio» tehát "egyenlővé tevést" jelent, úgy ahogy a «privatio» (privare=rabolni igéből) elrablást, elvevést jelent. A kiegyenlítés szó sokkal inkább fedné a fogalmat. "Egyenlet" így magában kissé színtelen. De minthogy, magunk sem tudunk jobbat javasolni, ne legyünk kritikusok s ne játsszuk a tagadás szellemét. A nyelvészkedést úgyis csak azért kezdtük, hogy a szó értelmét közelebbről meghatározzuk, mert jól tudjuk, hogy bevett szakkifejezések támadgatása mindenkor kissé visszatetsző.

Megállapítjuk tehát, hogy az egyenlet kifejezés alatt azt a követelést értjük, hogy valamit ki kell egyenlíteni, egyensúlyba kell hozni, vagy abban megtartani. Ostoba és felesleges volna a követelés, ha az egyenlőség már eleve fennállna. Csupán fenn kell állnia. És ezt éppen az x helyes megválasztásával érem el.

Még csak egy lépéssel sem jutottunk előbbre. Ismét ott tartunk, hogy valamely helyes értéket kell az x számára választanunk. Ez megint próbálgatást kívánna, pedig azt már határozottan elutasítottuk.

De még fennáll egy lehetőség az ismeretlen x számítással történő, egyértelmű, meghatározására: ha esetleg sikerül valamennyi x-et az egyik oldalon, minden egyebet a másikon összegyűjteni, akkor végül x=a, vagy nx=b alakú egyenletet kell kapnom.

Ha már idáig eljutottam, meglenne oldva a problémám. Mert x=a maga a megoldás, és nx=b, számpéldán 3x=9 könnyen kibogozható. Ha ugyanis 3x=9, akkor x bizonyára 3. Vagy általánosan nx=b esetén x=b/n.

De amíg ehhez a végső alakhoz jutok, amely ráadásul arról is biztosít, hogy nincsen más megoldás, addig minden valamelyest is bonyolult egyenlet annyi változást szenved, hogy csupán a józan észre támaszkodó számolgatás nem elégséges. Sürgős szükségem van valamilyen általános érvényű algoritmusra, minthogy, különösen általános számok esetén, azonnal oly labirintusban találom magam, ahonnan nem látszik kiút. A történelemben is hosszú volt az algoritmus megtalálásának az útja. Teljes biztonságot az egyenletek tana terén csak a XVII. és XVIII. században kifejlődött algebrával nyertünk.

De még mielőtt az algoritmus felfedezésének látnánk neki, világosan le kell valamit szegeznünk. Minden egyenletben kétféle, a számoknak és mennyiségeknek egymástól nagy mértékben különböző, fajtája létezik. Az ismeretlen (Szándékosan beszélünk egyelőre mindenkor csak egy ismeretlenről), az x és az úgynevezett állandók, amelyek már a számítás elején is ismertek, vagy ismerteknek tekintendők. Ezt a lényegbe vágó különbséget, még mielőtt a számítási szabályokkal foglalkoztunk volna, példákkal akarjuk megvilágítani. Mert akinek nem válik vérévé az ismert és ismeretlen mennyiségek megkülönböztetése, az nem juthat előre a magasabb matematika felé. Az x és az állandók a számok teljesen eltérő fajtájához tartoznak, ha ezt az állítást meg szabad kockáztatni. Az állandók lomhák, tehetetlenek, konzervatívak. Az x viszont mozgékony, sokértelmű, mindaddig, amíg a helyes értékét meg nem találta. Akkor és csak akkor lesz az x egyértelmű és állandó szám. Kártyás előzőleg a Jolly Jokerhez hasonlítaná. Természetesen csak elvben. Mert egy bizonyos egyenletben az x értéke már eleve határozott, ha nem is ismerjük. A következő egyenletben

7x+19—4=10x

19 és 4 az állandók, 7x és 4x az ismeretlen többszörösei. A 7x+13x+9x—2x+25=106 egyenletben természetesen az ismeretlenre vonatkozó összeadásokat és kivonásokat el szabad végezni.

Hisz az x «alma» is, ha a nagyságát még nem is tudjuk. S fennáll az a követelés, hogy mindegyik x egy és ugyanazt kell, hogy jelentse. Ilyen követelések függetlenek attól, hogy a nagyságot ideiglenesen nem ismerjük. Mert ha azt állítom, hogy 3 állócsillag meg 5 állócsillag kivonva belőle 4 állócsillagot 4 állócsillagot ad, nem kell még tudnom a csillagok nagyságát. Egyszerűen egynemű mennyiségek aritmetikai összegéről van szó. Tehát 7x;+13x+9x—2x+25=106 ugyanaz, mint 27x+25=106, s bár utóbbi lényegesen egyszerűbbnek látszik, még mindig nem a keresett megoldás. A megelőző példában valamennyi állandó egy oldalon volt ugyan, de az x két kifejezését választotta szót az egyenlőségi jel, most ugyan együtt vannak az x-ek, viszont az állandók oszlottak szét az egyenlőségi jel két oldalán. Kétségbeejtő! Mint egy fal, úgy akadályoz az egyenlőségi jel tervem keresztülvitelében, hogy valamennyi x-et az egyik, valamennyi állandót a másik oldalra vigyem. Pedig ez adná a megoldást, vagy legalább is a megoldás lehetőségét.

De meg az is előfordulhat, hogy az egyenlet kizárólag betűkből áll. Sőt az egyenlet ilyen alakja a gyakoribb a matematikában. Például az ilyen

nx+a+b—c=d—mx.

Itt már teljesen csődöt mond képzelőtehetségem. Igaz, hogy azt állítom, hogy a, b, c, d, n és m már jóelőre ismertek, S csak azt kívánom, hogy az x ezen "állandók" valamilyen csoportosításaként jelentkezzék. Mondjuk így: x= (d-a-b+c)/(n+m); mellesleg megjegyezve, az egyenletnek történetesen ez a megoldása. De miként jutottam ehhez az általános számokból álló szörnyhöz? Számítgatással miként juthattam volna el hozzá? S miként bizonyosodhatom meg arról, hogy x-nek éppen ez az értéke felel meg a kiegyenlítési parancsának? Hasonlattal segítünk magunkon. Képzeljük el, hogy egyenletünk mérleg.

A mérleg egyik serpenyőjében, tegyük fel, ennyi és ennyi állandó és ismeretlen fekszik, vegyesen. Tekintve, hogy a kiegyenlítési parancsot kiadtuk, az egyenlet csak akkor igazi egyenlet, ha a mérleg egyensúlyban van. Tehát, ha valamit megzavartam az egyensúlyon, ismét gondosan helyre kell hoznom, mert különben áthágom a kiegyenlítési parancsot: maradjunk meg egyelőre hasonlatunknál és tekintsük az állandókat ismert súlyú tárgyaknak, mondjuk rézsúlyoknak, az ismeretleneket viszont ismeretlen súlyú tárgyaknak, mondjuk almáknak. (Természetesen fontos, hogy valamennyi alma súlya ugyanaz legyen, s ezt még akkor is tudhatjuk, ha egy-egy alma súlyát nem ismerjük.) Tehát feladatunk oda módosul, hogy miként határozhatom meg egy alma súlyát, ha jelenleg az almák és súlyok egy egyensúlyban levő mérleg két serpenyőjén vegyesen, össze-vissza hevernek. Szerkesszük meg mondjuk a 2x+15 = 3x+8 egyenletnek megfelelően mérlegünket.

Az egyik csészében 2 alma és 15 egydekás súly fekszik, a másikban 3 alma és 3 egydekás. S mostan cserélgessek, változtassak addig, amíg meg nem tudom, mennyi a súlya egyetlen almának, de a nélkül, hogy a mérleget egyensúlyából kibillenteném. A "mérleg nyelve" állandóan jelzi, nem sértettem-e meg a parancsot. A "ne zavard az egyensúlyt" csak azt jelenti, hogy ha a mérleg mégis kibillen, vissza kell hoznom helyére. Ha az egyensúlyt tökéletesen fenn kellene tartanom, egyáltalán nem nyúlhatnék semmihez.

Most végre — ez a végcél — azon leszek, hogy az egyik serpenyőben csak alma, a másikban csak súly legyen. Ezután meg fogom próbálni, hogy egyik oldalon csak egyetlen alma feküdjék.

Nyúljunk először a súlyokhoz. Ezek, mint tudjuk az "állandóknak" felelnek meg. Világos, hogy az egyensúly mitsem változik, ha mindkét oldalon ugyanannyi darab súlyt elveszek vagy hozzáteszek. Vegyünk el tehát egyelőre a jobboldali serpenyőből három súlyt és a baloldaliból szintén hármat. A mérleg ingadozott ugyan, de újból egyensúlyba jutott.

Most tehát ilyen:

Matematikai módon kifejezve:

2x+12=3x

Most már csak a baloldalról kell a két almát elvennem, és elértem célomat. Ismét ugyanazt a fogást alkalmazom és állítom, hogy mindkét oldalon el kell két almát távolítanom, hogy az egyensúly megmaradjon.

Most már ez a helyzet:

s matematikai jelentése, x=12, egyúttal egyenletünknek is a megoldása. Egy alma 12 deka súlyú.

Csináljuk meg az ellenőrző próbát. Eredeti egyenletünk így hangzott:

2x+15=3x+3.

Ha most x helyébe 12-t teszek, akkor a következőket kapom: 2∙12+15=3∙12+3 vagy 24+15=36+3, azaz 39=39, s ez nyilvánvalóan helyes.

Kizárólag szemléleti úton igen fontos szabály birtokába jutottunk. Tudjuk, hogy egyenlőség megmarad, egyenlet nem változik, ha az egyenlőségi jeltől jobbra és balra ugyanazt a mennyiséget adom hozzá, vagy vonom le belőle. Pontosan fogalmazva: egyenlőkhöz egyenlőket adva, egyenlőket kapunk ; egyenlőkből egyenlőket kivonva, szintén egyenlőket kapunk, bár ez természetesen mérleg és szemléltetés nélkül is világos.

A mérlegről alkotott képünket tovább is építhetjük. De többször már nem rajzoljuk le, bízunk a képzelőtehetségünkben.

S ekkor világos lesz, hogy semmi sem változik az egyensúlyi állapoton, ha mindkét mérlegserpenyő tartalmát egyidőben ugyanazon tetszésszerinti számmal megszorozzuk. Teljesen mindegy az egyensúly szempontjából, hogy egyik oldalon 1 alma és a másik oldalon 12 súly, vagy az egyik oldalon 7 alma, a másikon pedig 84 súly fekszik, feltéve, hogy az almák ugyanolyan nehezek mint a súlycsoportok. Közömbös továbbá az egyensúly szempontjából, ha az egyenlet két «oldalát» ugyanazon számmal elosztom, vagy ugyanarra a hatványra emelem. Egyenlet «oldala» alatt az egyenlőségi jel előtt vagy után álló, ismeretlen vagy ismert mennyiségek összességét értjük. 5x—4+16=2x+8 esetén (5x—4+16) a baloldala, (2x+8) pedig a jobboldala az egyenletnek.

Most megelégszünk elméleti eredményünkkel, hogy valamely egyenlet két oldalán egyidőben alkalmazott bármely ismert matematikai műveletünk (feltéve, hogy egyforma mértékben alkalmazzuk), az egyenlet lényegén, a két oldal egyenlő voltán mit sem változtat. A gyakorlatban ez kabbalisztikus varázslatként jelentkezik, mennyiségeknek egyik oldalról a másikra történő átvitelében és az ismeretlen x izolálásában. Legyen mondjuk a következő egyenletünk:

5x—4+16=2x+8,

akkor először a baloldalon a (—4+16)-ot 12-vé vonom össze és akkor

5x+12=2x+8

alakú az egyenlet.

Most mérlegünk mintájára megpróbálom, valamennyi «állandót» az egyik, valamennyi "ismeretlent" a másik oldalra juttatni. Ezen célból először mindkét oldalon levonom a (2x+8) kifejezést.

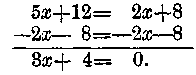
Most valami ijesztő dolog történt. (3x+4) nullával egyenlő. Vajon azt jelenti ez, hogy minden elpárolgott? És az x is nulla lett? Türelem! Ezt biztosan nem jelentheti. Mert még találhatok kivezető utat. Mindenekelőtt még nincsen valamennyi x az egyik és valamennyi állandó a másik oldalon. 

Most tehát mindkét oldalon vagy 3x-et vagy 4-et kell levonnom, hogy ez a szétválasztás megtörténjék. Próbáljuk meg a 4-et.

Az eredmény 3x= -4, s örömmel látom, hogy a gyanús 0 megint eltűnt. Most közvetlenül az egyenlet megoldása előtt állok. Már csak az x-et kell «izolálnom». Mivel a baloldalon 3x; áll, x-et úgy kaphatom meg, ha 3-mal osztok. De a «mérleg-szabályom» szerint ugyanazt az osztást a jobboldalon is el kell végeznem, hogy az egyensúly megmaradjon. Tehát:

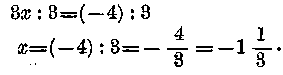
Megoldottuk az egyenletet. Most azonban lássuk, helyesen oldottuk-e meg. Ezért helyettesítsünk be az eredeti egyenletbe :

(Mindent közös nevezőre, 8-ra, hoztuk.)

16/3 = 16/3

A próba igazolja számításainkat.

Most már világítsuk meg az «átvivést», mert eszünkbe sem jut, hogy még egyszer ilyen nehézkesen számoljunk.

5x+12=2x+8.

Megint az előbbi egyenletet használjuk. És megjegyezzük, hogy az is eredményre vezet, ha megkíséreljük, hogy a 2x-et az 5x-hez és a 12-t a 8-hoz vándoroltassuk. De miként? Nos, nagyon egyszerű. Mindkét oldalon egyszerre le kell vonnunk 2x-et.

Mivel ezáltal jobboldalon teljesen eltűnik, csak baloldalon írjuk a kivonást. Tehát:

5x—2x+12=8, vagyis 3x+12=8.

Most a 12-t vándoroltatom. Ez 12 mindkét oldalon történő levonásával lehetséges. Ezzel a baloldalról eltűnik teljesen, a levonást csak a jobboldalon kell kiírnunk. Tehát:

3x=8—12, vagyis 3x=—4.

Most még az x együtthatója, a 3, menjen át a másik oldalra. Ehhez mindkét oldalt 3-mal kell osztani. A 3 ezzel a baloldalon eltűnik, s a jobboldalon jelenik meg mint osztó. Az eredmény

x = (—4) : 3 = -4/3 = —1 1/3.

Készen vagyunk. Megvan a szabály. Így szól: ha valamely mennyiség keresztülmegy az egyenlőségi jelén, az operációs parancs ellenkezőjére változik. Tézisből lizis lesz, lizisből tézis. Konkrét módon: összeadásból kivonás, kivonásból összeadás, szorzásból osztás, osztásból szorzás, hatványozásból gyökvonás, gyökvonásból hatványozás. (Ezzel csak később foglalkozunk.)

Most már urai vagyunk minden egyenletnek, ha az lineáris, vagyis az ismeretlen benne csak az első hatványon fordul elő. Annak, hogy az ilyen egyenletet miért nevezik "lineárisnak", később kapjuk geometriai magyarázatát.

Az olvasóra bízzuk eddigi feladatainknak új algoritmusunk szerinti újólagos kiszámítását. Mi azonban megvilágosításul bonyodalmasabb feladatokat számolunk át. Ilyen:

5(x—2)—2x=2(x—1)

5x—10—2x=2x—2

3x—2x = —2+10

x=8

Példa csak betűkkel:

Ehhez a feladathoz csak azt akarjuk megjegyezni, hogy mindenkor szabad az egész egyenletet megfordítani, illetve a két oldalt felcserélni. Hisz az x=5 és 5=x állítás ugyanazt mondja. Ez már az egyenlőségi jel lényegéből következik. Ugyancsak szorozhatok mindkét oldalon (—l)-gyel és ha eredményként esetleg azt kapom, hogy (—x)=(—10), írhatom, hogy

(—x) • (—1)=(—10) • (—1)

vagyis

x=10.

Ilyen szorzást ott alkalmazunk, ahol az x negatív alakban jelentkezik, minthogy engem a pozitív x érdekel. Tegyük fel, hogy valamily számítás eredménye (—x)=(±a), ez azt jelenti, hogy x vagy plusz a-val, vagy mínusz a-val egyenlő, akkor felírom, vagy csak gondolom,

(—x) • (—l)=(±a) • (—1)

vagyis

x=±a.

Vegyük figyelembe, hogy most az a mellett felül van a mínusz és alul van a plusz. Mert (+a)(—1) = —a, (—a)(—1)=(+a). Tehát az a előtti mínusz az első, az a előtti plusz a második szorzás eredménye.

Vannak olyan esetek is, amelyeknél az egyenlet olyan, mintha számunkra hozzáférhetetlen volna, mivel az x elsőnél magasabb hatványát tartalmazza. Ilyen pl.

(x+1)(x—l)=x²+x+1

Ez a látszólag másodfokú, kvadratikus egyenlet a kiszámítás során ártatlan lineáris egyenletnek bizonyul.

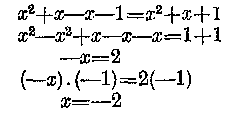
Látszólag ugyancsak igen veszélyes az

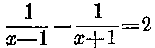
egyenlet is. Itt az x csak a nevezőben fordul elő. Lépésről lépésre haladunk: először közös nevezőre hozzuk a baloldalt.

vagy ami ugyanaz

Itt valóban másodfokú egyenletre akadtunk, s még nem tudjuk megoldani, mert a gyökvonást még nem ismerjük. A megoldás

... volna. További példa:

Általános megjegyzés: egyenletekkel való számolás a matematikában igen fontos dolog. Nagyon sok számítási előny, fogás létezik ezeknél. Az «egyenlet-gépezetet» minden matematikusnak úgy kell ismernie, hogy az «átvivést» az "izolálást" szinte álmában is el tudja végezni. Minden matematikai tankönyv számtalan ilyen válogatott példát tartalmaz. Különösen ajánlható Eulernek már ismételten említett kitűnő algebrája. Nyomatékosan ajánljuk, minthogy a matematikában nincsen "királyi út", lehetőleg ilyen egyenletek százainak megoldását, sőt feladatok készítését. Ez a foglalkozás legalább olyan érdekes, mint a keresztrejtvényfejtés, vagy a kártyázás. És kifejlődik közben az a bizonyos hatodik érzék, amelyet a laikus a matematikusban oly sokszor megcsodál. Az ész matematizálása majdnem fizikai jelenség, amint szinte tudat alatti módon magától értetődő az úszás, a kerékpározás, a helyes ütés a teniszben. Röviden: a matematika nagyon magas fokig tisztán gyakorlat dolga. Mindaz, amit gyakorolni nem lehet, vagy alig, az a matematikának olyan magas részéhez tartozik, amely minket, újoncokat, aligha érint. Nem akarunk mi Moltke-k, Napoleon-ok lenni, legfeljebb jóravaló tisztek. De — és ez a legnagyszerűbb tudományunkban — sohasem lehet tudni, hogy nem találunk-e éppen mi, ihletett pillanatunkban valami rendkívülit. Aligha valószínű, de kizárva nincs.

De csökkentsük ismét önérzetünket és fojtsuk el álmainkat a "tarsolyunkban levő marsallbotról". És számítsunk végig, mielőtt még az egyenlet fogalmát kiterjesztenénk, egy úgynevezett szöveges, vagy alkalmazott feladatot.

Egy apa jelenleg 48, fia pedig 21 éves. Hány éves volt a fiú, amikor apja tízszer olyan idős volt mint ő? Hány évvel ezelőtt volt az apa tízszer olyan idős mint a fia?

Ilymódon következtetünk: az apa és a fiú közti korkülönbség 27 év. Ez a mennyiség változatlan marad, tehát az egy állandó. Jelölje x a fiú korát abban az időben, amikor az apa tízszer olyan idős volt, mint ő, az apa pedig abban az időben (x+27) éves volt. Feladatunk szerint azonban akkor az apa tízszer annyi idős volt mint a fia, tehát 10x éves. Következésképpen x+27=10x, és ezzel "felállítottuk" az egyenletet. Most már nem törődünk azzal, hogy mit

jelentenek a mennyiségek, nyugodtan rábízzuk magunkat algoritmusunkra.

x+27=10x

27=9x