EGMONT COLERUS

AZ EGYSZEREGYTŐL AZ INTEGRÁLIG

AMIT A MATEMATIKÁBÓL MINDENKINEK TUDNIA KELL

HUSZONKILENCEDIK EZER

FRANKLIN-TÁRSULAT BUDAPEST

TARTALOM

Bevezetés

1. fejezet. "Igaz kabbala"

2. « A tizesrendszer

3. « Nem-tizes számrendszerek

4. « Szimbólumok és parancsok

5. « Kombinatorika

6. « Permutációk

7. « Szorosabb értelemben vett kombinációk

8. « Variációk

9. « Első lépések az algebrában

10. « Algebrai írásmód

11. « Algebrai műveletek

12. « Közönséges törtek

13. « Egyenletek

14. « Határozatlan egyenletek

15. « Negatív és tört hatványok

16. « Irracionális számok

17. « Törtrendszerek

18. « Függvények (Algebrai levezetés)

19. « A Pythagoras-tétel

20. « Szögfüggvények

21. « Imaginárius számok

22. « Koordináták

23. « Analitikus geometria

24. « A kvadratura problémája

25. « A differenciál és az ívhosszúság mérése

26. « A differenciálhányados és az integrál összefüggése

27. « A háromféle semmi

28. « Binomiális tétel

29. « Archimedes parabolakvadraturája

30. « Sorok

31. « A differenciálszámítás technikája

32. « Maximumok és minimumok

33. « Az integrálszámítás technikája

34. « Középértékek és határozatlan integrál

35. « További kvadratura feladatok

36. « Logaritmus

37. « Interpoláció. Extrapoláció. Befejezés

BEVEZETÉS

Egérfogó a matematika. Ha benne vagy, nehezen találsz utat, amely korábbi, matematikától mentes lelkiállapotodba visszavezetne. Hosszadalmas volna, ha ennek a jellegzetes tünetnek okát akarnánk adni. Így tehát csak a következmények megállapításával fogunk foglalkozni.

Ennek az "egérfogó tulajdonságnak" első következménye : kevés a matematikus pedagógus. Ritkán egyesül a matematikai tudás könnyen érthető előadásmóddal. Ebből ered rögtön a második következmény : művelt emberek és művelődni vágyók "matematikai alacsonyabbrendűség-komplexum"-a.

Senki se értsen félre. Nem támadni akarok, ellenkezőleg: védekező állást foglalok el. Mert rendkívül szokatlan, hogy laikus merészelje a tudományok legszigorúbbikát magyarázni.

De mivel jól megfigyeltem saját szenvedéseimet és láttam iskolatársaim küzködését, megérett bennem az az elhatározás, hogy matematikai élményeimet tudásomnak már valamely alacsonyabb fokán feljegyzem Hisz az «egérfogóról» kialakult meggyőződésem szerint jogos a félelmem, hogy néhány év múlva magam sem találom meg a kivezető utat.

De még egy másik nyomós ok is késztetett vállalkozásomra. Minden tudományba, de mindennapi életünkbe is egyre mélyebben hatol be a matematika és a matematikai módszerek és fogalmak. És semmiképpen sem kielégítő — majdnem kultúrbotránynak nevezném — hogy egy félig-meddig komoly értekezés olvasója egyszerre hieroglifák egész birodalmával kerülhet szembe, amelyek megijesztik és elrettentik az olvasástól; de megtörténhetik, hogy a kevés számú beavatott gúnyos mosolyát kel! zsebretennie. Nem a relativitás és kvantumelmélet matematikai magasságairól van szó, ilyen eset bármelyik közgazdasági vagy orvosi lapban is előfordulhat. A statisztikát ne is említsük, az ma már — elsősorban az angolszász országokban — teljes egészében matematika. Belopózott azonban a matematika hétköznapi nyelvünkbe is. Az újságok «középértékekről» írnak, «átlag-hőmérsékletet», "maximális teljesítményt", "görbék kritikus pontjait" és "erőtereket" emlegetnek: csupa olyan kifejezés, melyet a köznyelv a matematikától és a matematikai fizikától kölcsönzött.

Felesleges, hogy ilyen szavakat értelmetlen zörejként hallgassunk végig, sőt hatásukra magunkat kisebbértékűnek, esetleg műveletlennek tartsuk. Nagyszerű az ilyen szavak jelentése s ugyanannyira jelképes is, de felfogható és megtanulható.

Egyet mindenesetre feltételez könyvünk : bizonyos, tanulásra szánt és nélkülözhetetlen fáradozást. A monda szerint Ptolemaios Philadelphus király, Krisztus születése előtt 300 körül, megkérdezte a legnagyobb görög matematikust, Euklidest, miképpen lehetne a matematikát "könnyen" elsajátítani. A matematikus bátran felelte : "Királyok számára sincs külön út a matematikában!" Mindenkinek, aki csak felületesen is ismeri ezt a tisztán szellemi eredetű és lépésről lépésre felépülő tudományt, igazat kell adnia a nagytudású görögnek. De ne essünk kétségbe : "királyok útja" és "Himalája megmászása" közt, a folytonosság törvénye szerint, még számtalan középút is van.

Nagyérdemű és kiváló tudósok, így például Georg Scheffers, S. P. Thompson és Gerhard Kowalewski, teljes mértékben megértették és átérezték ezt a helyzetet és mindent elkövettek, hogy közbülső fokozatokat teremtsenek. Mindhárom kiváló pedagógus műve kultúrkincs. S mi sem áll távolabb tőlem, mint a merészség, hogy Scheffers plasztikus előadásmódjával vagy Kowalewski precizitásával, eleganciájával, akár pedig Thompson gazdag humorával versenyre keljek. De — és ez a «de» a lényeg — mindhárom mű feltételez valamit, amit nem volna szabad, ha teljesen le akarja küzdeni az olvasó alacsonyabbrendűség-érzetét: gimnáziumi műveltséget feltételez mindegyik, vagy legalább is a matematika elemeinek ismeretét. Magamon éreztem leginkább, — amikor statisztikai előadásokon vettem részt — hogy a matematika szeretete és a valaha elsajátított tudás mellett is mennyire fogyatékosak lehetnek ezek az elemi ismeretek. Élményem hatására vágtam neki, őszinte tisztelettel és becsüléssel a valódi tudomány iránt, merész kísérletemnek. Észrevettem ezenkívül, hogy háromféle indok is késztethet arra valakit, hogy ilyen könyvet saját használatára összeállítson, vagy kartársától segítségül készen megkapjon. Először is célja lehet valamely elfoglalt embernek, talán orvosnak, közgazdának, kereskedőnek, iparosnak, hírlapírónak, természettudósnak — de katonának, hivatalnoknak, alkalmazottnak, munkásnak, iskoláslánynak vagy fiúnak éppen annyira, hogy a matematikát, az egyszeregytől az integrálig az iskoláétól lényegesen különböző szempontból ismerje meg és közben a legáltalánosabb ismereteket elsajátítva belső megnyugvást találjon. Megeshet, hogy az előbbi elfoglalt ember többre vágyik. Szerény bevezetésem alapján akkor nyugodtan rábízhatja magát Scheffers, Thompson vagy Kowalewski erős vezető kezére és olyan mélyre hatolhat velük a matematikában, amennyire csak akar; míg csak maga is benne nem ül az «egérfogóban» és már nem érti, mire való volt az én szószaporításom és naivitásom. Ilyen olvasómra lennék a legbüszkébb, még akkor is, ha utólag mélyen megvet. Megtörténhetik végül, még hogy tanulók használják titokban könyvemet, mint tiltott segédeszközt. Kérem a pedagógusokat, ne vádoljanak azzal, hogy "elrontom az ifjúságot", ünnepélyesen kijelentem már itt, ezen a helyen is, hogy ellentmondások esetén nem nekem van igazam, ne nekem, hanem hivatott tanáruknak adjanak hitelt.

Tanárokról szólván: nem mulaszthatom el e helyen sem ama kellemes és elkerülhetetlen kötelességemet, hogy köszönetet ne mondjak dr. Walther Neugebauernek, a kiváló matematikusnak, aki a már említett tanfolyam előadójaként elvezetett a matematika kellős közepébe és megvilágította előttem ennek a tudománynak igazi nagyságát. Novalis, a költő írja: "Az istenek élete matematika. Isteni küldött csak matematikus lehet. A tiszta matematika voltaképp vallás. Csak matematikus lehet boldog. Az igazi matematikus magából merít lelkesedést. Lelkesedés híján nincs matematika".

Nagyon boldoggá tenne, ha csak leheletnyit is közvetíthettem ebből a felfogásból olvasóimnak. Mert fájdalom, a matematikai alacsonyrendűség érzése, mint minden hasonló érzés, gyűlöletet és ellenszenvet vált ki. A kitűnő görög Hypatiát, az egyetlen nőt, akinek a matematika őstörténetében szerepe volt, bizonyosan nemcsak vallási okokból kövezte meg a tömeg; és a matematika következetes és kérlelhetetlen ellenségei szerint rossz szolgálatot tettem a nagy Leibniznek, midőn merészkedtem kiemelni és sikerrel bemutatni zsenijének középpontját, a matematikát.

Bárcsak ez a könyv is hozzájárulna ahhoz, hogy a matematika, a tudományok legszentebbike, iránt érzett ellenszenv csökkenjen. Felületes emberek sokszor tartják a matematikát a materializmus csúcsának. Ezek nem tudják, hogy a matematika nemcsak az indus, babyloni és egyiptomi papok szemében volt a vallás rokona. Nem tudják, hogy Pythagoras, Cusanus, Pascal, Newton, Leibniz — csak néhány nevet említve a sok közül — éppen a matematikából merítették azt a megismerést, hogy minden tudományok «legbiztosabbjának» ködbevesző határai tesznek valóban hívővé és alázatossá az Isten iránt.

Sokszor fogunk még együttes haladásunk folyamán ilyen problémákra bukkanni. Most még csak röviden könyvem "szereposztásáról" számolok be : egyedül, magam írtam ezt a könyvet, amennyire erről az évezredes együttműködéssel felépült matematikában egyáltalán szó lehet. A matematikus dr. Walter Neugebauer, — bíráló olvasóim megnyugtatására említem — gondosan átnézte, és sok értékes tanáccsal szolgált, de azért távol álljon tőlem, hogy a felelősségnek akár csak kis részét is rá, a kiváló szakférfiúra, hárítsam.

Köszönettel kell még adóznom Hans Strohofernek, a Wiener Künstlerhaus festőtagjának is, hogy nem tartotta méltóságán alulinak adataim nyomán a szövegábrák megrajzolását.

És most — mert tudjuk, királyok számára sincs külön út a matematikában — olvasónak és írónak együtt kell dolgoznunk, szorgalmas munkával, hogy eljuthassunk az egyszeregytől az integrálig. Én remélem, hogy megadtam hozzá az elvi lehetőséget, a többit majd megmondják rosszakaróim.

EGMONT COLERUS.

ELSŐ FEJEZET

«Igaz kabbala»

Beteg üldögél az orvos várószobájában. Sejti, hogy nem kerül egyhamar sorra, így olvasmánnyal akarja idejét eltölteni. Az asztalon gyógyintézetek és hajóstársaságok tarka füzetei hevernek. Egyik kép különösen megragadja figyelmét, déli tengerek és trópusi városok pompája árad róla. Kíváncsian nyitja ki a könyvecskét, de csalódott. Érthető szót is alig talál benne. A prospektus látszólag délamerikai hajójáratot dícsér, de — betegünk ezt sem tudja bizonyosan — alighanem portugál nyelven. Mégsem teszi le. A kabinok, éttermek, az érintett kikötők képei szépek és érthetők is. De még mást is megért, anélkül, hogy fordításra lenne szüksége: a hosszú számoszlopokat, táblázatokat, közbeiktatott számításokat, érkezési és indulási adatokat.

Előre látom, hogy példámat gyerekesnek, magától értetődőnek, esetleg éppenséggel ostobának találják. Ki vonta valaha is kétségbe, — mondják — hogy ma majdnem valamennyi művelt nemzet ugyanazokat a számjegyeket használja? Mi volna ebben talányos vagy csodálatos? Kár volt a bevezető mondatért. A 3-as számjegy portugál szövegben ugyanazt jelenti, mint németben vagy angolban. És az 5214x7=36 498 számítás is független az országtól, amelyben végrehajtották. Ennyi az egész!

Készségesen elismerem, hogy e méltatlankodó bizonyítás és, eredménye ellen keveset vagy inkább semmit sem lehet felhozni. Csupán az ellen tiltakozom, hogy a tárgyalást is lehetetlenné teszi. Sőt állítom, hogy az ostoba példa behatóbb vizsgálata egyenesen a matematika legbelsőbb rejtélyei felé vezet és számos igen fontos alapfogalom megismerését teszi számunkra lehetővé.

Ellenfelem figyelmét ugyanis elkerülte valami. Mindenekelőtt csak jelentésében azonos a német olvasta dolog a portugál által olvasottal, feltéve, hogy mindkettő a számokkal foglalkozik. Mert a portugál más szót használ a számjegyek kimondására, mint a német. Svédek, angolok, franciák ismét más szavakat. A számok kimondásának módja a számrendszerek titkáig vezet. Németül például a vier-und-zwanzig kifejezést használjuk, ha a 24 jelet látjuk, tehát a négy-és-húsz szóösszetételt. Az angol viszont a twenty-four, húsz-négy szavakat látja benne. A francia a nyolcvanat nem octante-nak nevezi, mint logikusan következnék trente, quarante stb. után, hanem szorzásszerű szóképzéssel, quatre-vingt, azaz «négy-húsz» kifejezéssel lep meg.

Első eredményként tehát megállapíthatjuk, hogy nemzetközi számjegyírásunk betűírásunkkal csak ritkán függ közvetlenül össze és mindenekelőtt mások az alapelvei. A számjegyírás magában véve tiszta fogalomírás, míg betűink önmagukban nem fogalmaknak, hanem csupán hangoknak jelképei. Csak később, szavakká összeillesztve lesz belőlük fogalmak szimbóluma. Ez a fogalom: 3 — a számjegyírásban egyetlen jelet kíván. Betűírásban már a német drei a d, e, i és r betűk bizonyos meghatározott sorrendjével fejezhető ki. Sőt a francia trois vagy a magyar három már csupán öt betűvel tudja ugyanazt megjelölni.

De még csak az elején vagyunk. A számok hegységének lábánál állunk és készülünk felkapaszkodni. Eddig csupán számokról és számjegyekről beszéltünk, de szavunk sem volt arról a csodálatos, számrendszernek nevezett építményről, amely az emberi szellem legnagyobb büszkesége lehet. Ellenfelem újabb gáncsoskodása ismét könnyen érthető, így szól ugyanis : «Ha számrendszeren azt érted, amit minden gyerek az elemi iskola első osztályában tanul, tehát a tizes számrendszer írásmódját, akkor kérlek, hagyj inkább békében. Ismerjük, minden nap alkalmazzuk és semmi kedvünk, hogy írásvágyadat érdeklődésünkkel még fokozzuk is. De ha számelmélettel akarsz traktálni, Gauss, Dirichlet, Dedekind, Kronecker és más nagy tudósok vizsgálataival, akkor vedd tudomásul, már itt becsapjuk a könyvet és visszaadjuk a könyvkereskedőnek. Mert ez esetben nem tartottad meg ígéretedet, azt, hogy elfogulatlanul csak a legszükségesebbet adod elő».

"Helyesen szóltál, ellenfeleim, válaszolom erre. «Csak azt felejted el, hogy amit a számrendszer titkairól elmondok, egyáltalán nem öncél. Távolról sem gondolok arra, hogy valódi számelméletet kezdjek előadni. Még kevésbé csak azt, hogy miért írjuk a kétezerötszáztizennégyes számot éppen így : 2514. Helyesebben, nem akarok ilyen magyarázatoknál időzni. De mivel semmilyen előzetes tudást sem szabad feltételeznem, közismert dolgokhoz kell fejtegetéseimet kapcsolnom, hogy mindjárt az első fejezetben érthetővé tehessek igen nehéz matematikai fogalmakat. Megszakítom tehát párbeszédünket, hogy folyamatosan végezhessem vizsgálódásainkat".

Idézzük a szellemtörténet egyik legnagyobb alakjának, Gottfried Wilhelm Leibniznek (1646—1716) a panhisztornak, mindentudónak szavait. Tudjuk, Leibniz nagy matematikus is volt és az úgynevezett infinitézimálszámítás, vagyis "felsőbb matematika" egyik úttörője. Szóval Leibniz szimbólumokra (népszerűen azt mondhatnánk "nagyjelentőségű jelekre") vonatkozó általános tételeit «cabbala vera» igaz kabbala néven említi. Alighanem mindenki tudja, mit jelentenek a kabbala, kabbalisztikus kifejezések. Mágia, varázslat, ráolvasás, szavakkal és jelekkel felszabadított misztikus erők tartoznak a kabbala fogalma körébe. És a matematikai jelek igen lényeges, súlyos részei a Leibniz-féle szimbólumszámításnak, ennek az általános tanításnak a szimbólumokról.

Tudom, hogy ez az első utalás Leibniz gondolatmenetére nem lehet teljesen érthető. Így tehát Leibniz kijelentését a magunk számára egyszerűsíteni fogjuk és csak annyit jegyzőnk meg, hogy a matematikai írásmód önmagában véve is valamelyes "igaz kabbalát" rejt. Világosabbá teheti gondolatmenetünket egy kis kirándulás a matematika, helyesebben a számjegyekkel való számolás történetébe. Nincs igaza ellenfelemnek, ha a tizes számrendszert oly becsmérlőn említi. Mérhetetlen és kimondhatatlan érdeme ennek a rendszernek, hogy minden elemista megtanulhatja. Mert a történelem távlatában másik képét is látjuk. Ami ma elemi iskolai tanulóknak való feladat, az néhány évszázaddal ezelőtt pálya díjjal jutalmazott feladvány volt a legnagyobb matematikusok számára. Hiányzott még ugyanis az a szinte önműködő gép, a számrendszer, a helyes írásmódban rejlő igaz kabbala.

Engedelmet kérek, hogy kissé eltérhessek itt a tárgytól. A helyes írásmódról volt szó. Igaz, a rendszer egészére vonatkozott. Az "írásmód" kifejezés e magasabb értelmezésén kívül arra is szeretném felhívni a figyelmet, hogy a matematikai jelek ismerője is csak akkor tud könnyen és biztosan e jelekkel bánni, ha szem előtt tart két közhelynek tetsző szabályt. Szépen, lehetőleg áttekinthetően kell írnia. Ne huzigáljon át, ne írjon keresztül-kasul semmit és ne firkálja tele a közöket és lapszéleket mellékszámításokkal. Másodszor, a kezdő — és ez a kezdő állapot messzire terjed tudományunkban — ne ugráljon át türelmetlenül közbenső műveleteket és a mellékszámításokat ne fejben végezze el. A kabbalára szántuk magunkat és a varázsjelek írásban akarnak élni. De ha valaki lényegesnek tartja, hogy tudása minden fokán fejben is végezzen számításokat, képzelőerejének kipróbálására és gyakorlására, akkor végezzen számításokat mondjuk elalvás előtt, jegyezze fel az eredményt és ellenőrizze őket másnap lépésről-lépésre az igaz kabbala segítségével. Ez szinte sportszerű tanács. A vívásnak, boxolásnak, tenisznek oktatója is minden ütést és vágást a legnagyobb pontossággal, részletről részletre, szinte lassítva ismételtet. A személyes stílus és az egyéni tempó az alapfogalmak csiszolódása folyamán amúgy is, magától is kifejlődik.

De térjünk vissza tárgyunkhoz. Említettem, hogy a mai. számjegyekkel való számolás egyáltalán nem volt mindenkor magától értetődő. Csak a Krisztus utáni tizenkettedik században lett az igaz kabbala a nyugati népek közkincse. Egyszerűség kedvéért ismét említsük meg, hogy akkoriban a számolás két rendszere küzdött az elsőségért. Az abakuszosok iskolája és az algoritmikusok iskolája. Abacus a neve az ókorban is használt számolótáblának. Olyan táblát kell elképzelnünk, amelyet függőleges vonalak részekre osztanak. Minden oszlop egy-egy fokszámot jelképez, tehát egyeseket, tízeseket, százasokat, ezreseket stb. Ha számolni akarunk az abakuszon, minden oszlopba a megfelelő számú követ vagy táblácskát kell tennünk. Tegyük fel, hogy 504,723-hoz 609,802-t kellene hozzászámlálnunk, hozzáadnunk.

Láthatjuk, hogy a fehér táblácskákhoz (első szám) a fekete táblácskákat (második szám) hozzászámlálva a helyes 1,114,525 eredményt kapjuk. Nullát ez az abakusz számítás még nem alkalmaz. S figyelembe kellett még venni, hogy 15 százas egy ezressel és 5 százassal, 14 ezres egy tízezressel és 4 ezressel és végül 11 százezres egy millióssal és egy százezressel azonos.

Ne foglalkozzunk most behatóbban az abakuszosok művészetének, a számolótábla használatának szabályaival. De nem esik nehezünkre belátni, hogy az algoritmikusok iskolájának feltétlenül győznie kellett.

Most már oly ponthoz jutottunk, amely megérdemli teljes figyelmünket. De előbb egy szót kell megmagyaráznunk. Algoritmus (algoritmikus) egy névnek eltorzult alakja. Muhammed ibn Musa Alchvarizmi nevét rejti. Ez a kelet-arábiai matematikus Khorasszanból származott és később Bagdadban élt. 800 és 825 között Kr. u. többek közt könyvet írt az indiai (mai nevükön arab) jelekkel, ill. számjegyekkel történő számolásról. Mégpedig a helyértéket alkalmazva, ő már ismerte a nullát, kis körnek rajzolta. Különféle utakon, a keresztes hadjáratok során, de a Toledoban, Sevillában, Granadában működő arab főiskolák útján is, megismerték a nyugat tudósai is, latin fordításban, az arab munkákat, köztük Alchvarizmi könyvét az indiai számjegyekről. Ismételjük : az algoritmikusok algoritmus néven az indiai számrendszert, a helyérték figyelembevételét honosították meg a nyugati tudományban. Ez volt az első lépés az igaz kabbala felé. S többé nem az esetlen számolódeszka szolgáltatta a számolási műveletek eredményét, hanem egy bizony titokzatos varázsírás tette lehetővé a legbonyolultabb és legnagyobb számítások csalhatatlan végrehajtását. Az egész varázslathoz mindössze tíz jel 0-tól 9-ig, egy darabka papír, toll és a kis egyszeregy ismerete volt szükséges.

Ma már aligha képzelhetjük magunkat azoknak a számolóknak a helyzetébe, akiknek nem kellett már számolótábla ahhoz, hogy például 85,243-at 9621-gyel megszorozzanak, hanem egy papírrongy is elegendő volt a szorzáshoz. A boldogság varázsos borzongása futhatott végig akkor a számolókon. És hányszor érezhették, hogy Bábel tornyának tetejére értek, ahonnan már kezükkel elérhetik az égboltot.

De kénytelenek vagyunk e történelmi ábrándozásunkból visszatérni hűvösebb világunkba. Egyelőre csak azt tudjuk, hogy az algoritmus szó bizonyos jelrendszeren alapuló írásos számolási eljárást jelent. Még pedig olyan zárt rendszeren belül, amely magában is feleslegessé teszi agymunkánk egy részét és hozzáférhetővé tesz olyan területeket, ahol képzeletünk már csődöt mond vagy legalábbis könnyen eltévedhet. Közelebbről kell tehát megvizsgálnunk, hogy honnan származik a varázsereje e különleges algoritmusnak, amelyet dekadikus, vagyis tizes számrendszernek hívunk.

MÁSODIK FEJEZET

A tízesrendszer

Ekkor először is a rendszer már jelzett hallatlan egyszerűsége tűnik szembe. Voltaképp tíz számjegy szimbólum az egész anyag, amivel dolgunk van. Ha ehhez még hozzáveszünk néhány összekapcsolási szimbólumot, mint a «több», «kevesebb», «szorozva» és «osztva» jelek (+, —, x, :) és végül hozzávesszük az egyenlőségjelét (=) is, akkor mint derék algoritmikusok már a numerikus számítás egy egész világán uralkodunk. Mindenesetre még valami további is hozzátartozik, mint egyik legfontosabb feltétel, algoritmikus mesterségünkhöz: az ú. n. helyértékrendszer, ami talán magától értetődőnek látszik, de maga a titok kulcsa.

Mint erőteljes példája a helyérték nélküli írásmódnak, álljon itt az ú. n. római számírás. Egy római «algoritmikust» fölszólítottak, hogy pl. csak adja össze az MDCCCXLIX és a MMCXXIV számokat. A tízeseknél és az egyeseknél a legnagyobb zavarba jön s kénytelen az abakuszhoz, a számolótáblához folyamodni, elismerve, hogy voltaképp semmiféle algoritmussal nem rendelkezik. Az indus rendszer algoritmikusa nem tartja érdemesnek fáradni az 1849 és a 2124 számok egymás alá való írásával sem. Néhány másodperc múlva már tudatja az eredményt, hogy az összeg 8978.

Foglalkozzunk most azonban közvetlenül a problémával. Helyértékrendszer alatt a számok oly írásmódját értjük, amely minden egyes számjegynek más-más értéket tulajdonít, ha a jegy más és más helyt áll. Akkor is ha ugyanarról a jegyről van szó. Éspedig, mivel a nagyságrend törvénye balról jobbra állapíttatott meg, pl. egy 3 az utolsó helyen 3, az utolsó előttin 30, a hátulról harmadik helyen 800, a hátulról negyediken 3000, és így tovább. Az ú. n. tizedestört-helyekről még nem beszélünk. Egyelőre csak egész számokkal foglalkozunk Kronecker mondására gondolva, hogy az egész számok Istentől származnak és az összes többi emberi mű.

A 3-ra vonatkozó példánkból már látjuk, hogy a helyérték jobbról balra minden egyes lépésnél megtízszereződik. Innen ered a tizedes- vagy dekadikus rendszer elnevezés. A tízet itt a rendszer alapszámának nevezik.

Ámbár hatalmasan elébevágunk a dolgoknak, mégis a következő fejtegetések egyszerűsítése végett egy új fogalmat vezetünk be. T. i. a hatvány fogalmát. Ennél voltaképp nincs másról szó, mint valamely számnak önmagával való szorzásáról, amit egy különösen rövid jellel írunk. Egyelőre azonban semmiképp sem foglalkozunk az ú. n. «hatványozással» vagy a "hatványra emeléssel", hanem néhány példa kapcsán csak az írásmódot világítjuk meg. Tízszer tízet a tíz második hatványának nevezzük és így írjuk: 10². Tízszer tízszer tízet a tíz harmadik hatványának nevezzük és így írjuk: 10³. 10x10xl0xl0=10⁴; 10x10x10x10x10=10⁵ stb. Természetesen e számokat ki is számíthatjuk. Így 10²=100, 10⁵=100,000, 5²=5x5=25, 6³=6x6x6=216, stb. Valamely szám első hatványa magát a számot jelenti, mivel mintegy csak egyszer lép föl a szorzásban. Tehát 10¹=10, 5¹=5, 29¹=29, stb. Az első hatványt, vagyis a kis egyest fölül jobbfelől, többnyire nem írjuk ki. De még egy hatványt kell bevezetnünk, amelynek különös eredményét e helyen nem magyarázhatjuk meg. T. i. az ú. n. zérusadik hatványt. Fölállítjuk tehát a követelményt, hogy valamely szám az önmagával való szorzásban egyáltalán ne forduljon elő mint tényező. Ennek jelentése mintegy 10° vagy szóval: tíz a zérusodik hatványon. Bárki jogosan jelentheti ki, hogy egy ily követelmény teljes értelmetlenség. «Szorozz valamit meg önmagával úgy, hogy a szorzásban egyáltalán ne szerepeljen, végezz egy számolást (még hozzá egy szorzást), amelyben az egyetlen megengedett tényező, t. i. az illető szám, zérus-szor, tehát egyetlenegyszer sem, szerepel. És mondd meg nekem az eredményt". Ez a kérdéstétel. Mint már említettem, egyelőre udvariasan bocsánatot kell kérnem és közlöm, hogy bármely és bármiféle szám (A 0° kivétel, mivel a 0 ebben az összefüggésben nem tekintendő számnak.) a zérusodik hatványra emelve, eredménytelenül egyet ad. Tehát 10°=1,25°=1,275,859°=1, és így tovább bármily nagy számoknál.

Tehát ismételve: bármely szám a zérusodik hatványon egyet ad, Az első hatványon önmaga. A második hatványon a szám önmagával szorozva. A harmadik hatványon a szám önmagával és még egyszer önmagával szorozva és így tovább. Jelesen a 10 szám esetén: 10°=1, 10¹=10, 10²=100, 10³=1000, 10⁴=10,000, ...

Jószemű ember e számsorozat szemlélésekor rögtön észreveszi, hogy a tíznél a kis számjegy jobbfelől fölül (az ú. n. hatványmutató vagy hatványkitevő) azon zérusok számát adja, amelyek tíz illető hatványában vannak. Bizonyára fontos és a számrendszerre nézve nagyon fölvilágosító összefüggés. De nem akarunk itt tovább vesztegelni, hanem most bátran behatolunk a számrendszer mélységeibe és magasságaiba. Mivel már kezünkben van az egész fölszerelés a mi számjel-algoritmusunk átkutatásához.

A számolódeszka megtekintésekor mindenki előtt világossá válik, hogy a tízesrendszer tetszőleges száma egyesek, tízesek, százasok, stb. bizonyos sokaságából áll. Arra törekszünk most, hogy alkalmas írásmódot találjunk, amely világosan megmutatja bármely szám belső szerkezetét anélkül, hogy segítségül kellene vennünk a merev abakuszt (számolódeszkát). Az előbbiek után nem lehet túl nehéz ezt az írásmódot kitalálni. Ez az ú. n. additív vagy szummatorikus sor, éspedig egy hatványsor. (A matematikában "sor" mindig számok vagy mennyiségek additív vagy szubsztraktív egymásmellé sorakoztatását jelenti.) A tudós kifejezések senkit se riasszanak el. Mert egy példa az eljárást rögtön megmagyarázza. Legyen pl. hogy ily sorba kell szétszednünk az 1,483,706 számot. Ezt minden további nélkül meg tudjuk tenni eddigi ismereteinkkel. Írjuk először is még primitíven:

6x1+0x10+7x(10xl0)+3x (10x10x10)+8x(10x10x10x10)+4x(10x10x10x10x10)+1x(10x10x10x10x10x10).

Erre nézve először is megjegyezzük, hogy bármely szám zérussal szorozva újra 0-t ad és hogy én ezért megfordítva minden zérust fölfoghatok mint valamely számnak és 0-nak a szorzatát. E megfordítást itt tudatosan fölhasználjuk a sornak a tízeshelyekre vonatkozó rendszeres kiegészítésére. Ezenkívül most még további egyszerűsítéseket alkalmazunk. Először elejtjük a nehézkes ferde keresztet (x) a szorzásnál és helyette a pontot alkalmazzuk, miként ez a matematikában általánosan szokásos. Azután a zárójelekben levő kifejezéseket megfelelő hatványokkal fejezzük ki. És végül megjegyezzük, hogy egy ily sorban a számjegyeket a hatványok előtt "koefficienseknek" (együtthatóknak) nevezik. 6, 0, 7, 3, 8, 4, 1 — röviden: a számunkat alkotó jegyek — a hatványsorban ezután csak mint "koefficiensek" szerepelnek. Vegyük egyelőre csak tudomásul ezt a fogalmat. Többet róla még nem mondhatunk e helyt.

Írjuk tehát most matematikailag helyesen:

1,483,706= 6·10°+0·10¹+7·10²+3·10³+8·10⁴ +4·10⁵+1·10⁶.

Ezzel teljesen és egyértelműen feltártuk a helyértékes tízesrendszer belső szerkezetét. Ennek a dolognak a megvilágítását, ú. n., «diszkusszió»-ját nem akarom az olvasóra hagyni, hanem — még hogy ha unalmas is — vele közösen akarom elintézni. Először is látjuk, hogy az ú. n. nagyságrendet megtartottuk. A tíz hatványai egymásután sorban következnek, mint 10°, 10¹, 10², 10³, stb. Ezen semmit sem változtatnak a koefficiensek. Mert még 9·10° (tehát 9·1=9) is mindig kisebb tartozik lenni, mint 0·10¹ (tehát 0·10=0), mivel ez a zérus a tízesek helyén semmi mást nem jelent, minthogy a számban legalább 10 tízes előfordul, mivel egy szám sohasem kezdődhetik zérussal. Szolgáljon például ez a szám: 109, amely mint sor írva a következő : 9·10°+0·10¹+1·10². Hogy 10° egyenlő 1, ezt már említettük. Világos továbbá, hogy a sor elméletben a, végtelenbe folytatható. Azaz nincs egyetlenegy még oly nagy szám, amely nem volna írható koefficiensekkel ellátott tízhatványok ily sorának az alakjában. Természetesen megfordítva minden olyan sor újra visszavezethető egy dekadikus számba. 5·.10⁰+0.l0²+ 8·10³+9·10⁴+3·10⁵ nem más, mint ez a szám: 398,075, t. i. még egyszer — szinte fölösleges módon — szavakban: 5 egyes, 7 tízes, 0 százas, 8 ezres, 9 tízezres és 3 százezres.

Szándékosan csak most említjük, hogy egy tökéletes számrendszer föltételezi még, hogy az ú. n. fokszámok (a tíz hatványai) tisztán nyelvileg saját nevükkel jelölhetők (tíz, száz, ezer stb.) A mi rendszerünkben nincs szigorúan keresztülvíve a dolog. Különös módon saját nevük csak 10¹, 10² és 10³ számára vannak, azaz tíz, száz, ezer. Tízezer és százezer már szorzatos összetételek. 10⁶, vagyis a milliónak van újra saját neve. Ezermillió (10⁹), vagy a milliárd a legközelebbi szigorú elnevezés. És azután következnek a millió hatványai szerint, a billió (1,000,000²=10¹²), a trillió (1,000,000³=10¹⁸), a kvadrillió (10²⁴), a kvintillió (10³⁰) stb. E szabálytalanság okát nézetem szerint a históriailag adódott gyakorlati szükségletekben találjuk meg. A pénz- és hadügy kezdetben csak ezerig terjedő felsőbb egységeket kívánt. És állítólag csak Marco Polo gazdagsága tette szükségessé a millió fogalmát. Az egészen magas egységeket (pl. billió stb.) a közönséges nyelvhasználat is «csillagászati szám»-oknak nevezi és így mutatja alkalmazási területüket és keletkezésüket.

Végérvényesen ismételjük tehát: a tízesrendszer összekötve a helyértékrendszerrel egy algoritmus. Lehetővé teszi nekünk, hogy az összes számítási műveleteket a legnagyobb könnyedséggel véghez vigyük az összeadásnál, a kivonásnál, a szorzásnál és az osztásnál, amelyek szabályait manapság már az elemi iskolában megtanuljuk. A tízesrendszer sajátos, a betűktől teljesen különböző fogalomszimbólumokból áll, amelyek a számértékeket jelentik 0-tól 9-ig. A rendszer alapszáma a 9-re következő szám, amelyet tíznek nevezünk és 10 által jelöljük. A további fokszámokra (a tíz hatványaira) részben saját nevekkel rendelkezünk, mint pl. száz, ezer, millió, milliárd, billió stb.

Most már oly magasra hágtunk a mi számhegyünkön, hogy egy végtelenbe nyúló, elágazó völgy, a tízesrendszer völgye fölött nyertünk kilátást és áttekintést. Megjegyezzük azonban, hogy még mindig igen mélyen a csúcs alatt vagyunk. Mit fogunk a csúcsról látni? Vannak-e még más völgyek is? Vagy magas fennsík a hegy, összeköttetés nélküli kősivatag?

Megpihenünk és tépelődünk. És eközben mindenféle nyugtalanító dolog jut eszünkbe. Mit jelent az, hogy pl. a német nyelvben az «elf» és a «zwölf» szavak szerepelnek, de utánuk «dreizehn» és «vierzehn» következik? Mit jelent a franciák talányos «quatrevingt»-je?. Ezek a tízesrendszer nézőpontjából rendszerbeli zavarok, kisiklások. Ebben a tekintetben nincs kétely. «Quatrevingt» (négy-húsz) kétségbeejtően hasonló szerkezetű, mint a német «vierzig». És "elf" és «zwölf» úgy látszanak, mint közvetlen folytatásai az «eins»-tól «zehm-ig levő számoknak. Miért nem mondanak «elf» helyett «einzehn)>-t és «zwölf» helyett «zweizehn»-t? Egyáltalán miért éppen a tíz az alapszáma a mi rendszerünknek? Kitűnteti talán valami a tízet más számmal szemben? Mintegy Isten áltál ajándékozott rendszer a tízesrendszer? Vagy talán csak az a tény okozta a tízesrendszer előnyben részesítését, hogy tíz ujjunk van és őseink egykor ujjukon számoltak?

De nem hagyjuk sokáig tépelődni számhegyünk vándorát. És odasúgjuk neki: a tízesrendszert semmi, de semmi sem tünteti ki elméletileg tetszőleges más alapszámú rendszerrel szemben. A történelem folyamán szerepelt már hatvanasrendszer, ötösrendszer, húszasrendszer és tizenkettősrendszer. Sőt a nagy Leibniz Rómában, az 1690-ik évben minden rendszerek legfigyelemreméltóbbját, a kettősrendszert (a diadikát vagy binar aritmetikát) fedezte föl, amely mindössze két számjegyet alkalmaz, a 0-t és az 1-et. És a mi «quatrevingt»-tünk valóban időszerűtlen maradéka egy kelta húszasrendszernek (ujjak meg lábujjak!), amely becsúszott a francia nyelvbe.

HARMADIK FEJEZET

Nem-tízes számrendszerek

Minthogy a tizesrendszer épületét, szerkezetét igen jól megismertük, merész kísérletként, teljesen önállóan, másik rendszert állítunk fel. Válasszunk először tíznél kisebb alap számot, legyen ez például hat. Felépítjük ezután, pontosan a tizes rendszer mintájára, új algoritmusunkat és majd meglátjuk, mire megyünk vele. Először csak egészen egyszerűen és érzés után: A tizesrendszerben tíz számjegyet — 0, 1, 2, 8, 4, 5, 6, 7, 8, 9 — használtunk. Ezek szerint,, következtetjük, hatosrendszerünkben hat számjegy, tehát 0, 1, 2, 3, 4, 5, elegendő lesz. De hogyan írjuk a hatot, a hetet, a nyolcat, a kilencet? Gondoljunk most hatványsorunkra. Az alapszám első hatványát így írtuk : 10¹. Vagy egyszerűen így: 10. Tehát az első kétjegyű szám volt. Tehát a hatosrendszerben is 10-nek írjuk az alapszámot, de ez itt nem tízet, hanem hatot jelent.

Elhiszem, hogy sok olvasóm zavarban lesz itt, mert azt hiszi, hogy a tizesrendszer isteni eredetű. Ezért lépésről-lépésre haladunk és elsősorban felírjuk a tizesrendszer első húsz számát egymás mellé és alájuk a hatosrendszer megfelelő első húsz számát.

1,2,8,4,5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20

1,2,3,4,5,10,11,12,18,14,15,20,21,22,23,24,25,30,31,32

Látható, hogy az írásmód ama tény közvetlen következménye, hogy a mindenkori számrendszerben másképpen nem is lehet írni. Öt számjeggyel és a nullával a hatot másképpen mint 10 nem tudom írni. Éppen olyan kevéssé, mint kilenc számmal és a nullával tizenkettő soha másképpen nem fejezhető ki mint 12.

Vegyük most szemügyre fokszámainkat. Értékük, tizesrendszerben írva 6°, 6¹, 6², 6³, 6⁴ stb. kell hogy legyen. Vagy továbbra is tizesrendszerben, értékük 1, 6, 36, 216, 1296 stb. Sorként írva tehát tetszésszerinti számot a hatosrendszerben így fejezhetek ki: 2x6°+4x6¹+0x6²+3x6³+5x6⁴ ami azt jelenti, hogy 2x1+4x6+0x36+8x218+5x1296. Tizes rendszerben írva ez 7154-et ad eredményül. Jegyezzük meg jól, hogy tizesrendszerben írva sem haladhatják meg az "együtthatók" értékei az ötöt, mert ez megsértené a nagyságrend szabályát és nem lehetne a számot hatosrendszerben felírni. Most egy merész fogás következik. Fel fogjuk írni a fent említett számot a hatos számrendszerben. Ehhez nem kell egyebet tennünk, mint az együtthatókat egymás mellé leírnunk. Mégpedig a legmagasabb hatványéval kezdve fogyó hatványok szerinti sorrendben. Számunk tehát, hatosrendszerben írva, ez lesz : 53,042. Tekintve, hogy ez nem jelent egyebet, mint ezt a kifejezést: 2x6°+4x6¹+0x6²+3x6³ + 5x6⁴, megállapíthatjuk, hogy 53,042 (hatosrendszer) ugyanaz, mint 7,154-gyel (tizesrendszer). Bár felesleges, megcsinálhatjuk még a próbáját is és sorokká bonthatjuk a két számot:

7154 (tizesrendszer) = 4x10°+5x10¹+lx10²+7x10³

58,042 (hatosrendszer) = 2x6°+4x6¹+0x6²+3x6³+5x6⁴.

azaz

4x1+5x10+1x100+7x1000 biztosan ugyanannyi, mint a 2x1+4x6+0x36+3x216+5x1296.

A számítás természetesen helyes. Mind az első, mind a második sor összege (tízesrendszerben írva) 7154-et ad.

De hagyjuk most már teljesen a tízesrendszert és írjuk fel az előbbi számot, 53,042-t (hatosrendszer) sor alakjában, de saját rendszerében. Ilyenformán a következőt kapjuk: 53,042=2x10°+4x10¹+0x10²+8x10³+6x10⁴,

de itt a 10 már nem a tízesrendszer tízét jelenti, hanem a tízesrendszerbeli 6 fejezi ki az értékét.

De lényegesen többet akarunk elérni. Lássuk tehát, használhatjuk-e a hatosrendszert is algoritmusként, vagyis alkalmas-e arra, hogy benne számolási műveleteket, jól ismert összeadásunk, kivonásunk, szorzásunk és osztásunk stb. mintájára elvégezzünk. Ehhez azonban még egy segédeszközt kell előkészítenünk. A hatosrendszer egyszeregyét. Első pillanatra egy őrült számtani gyakorlatainak látszik, De némi gondolkodás és egy pillantás a számoszlopokra, valamint annak a megfontolása, hogy most csak hat számjegy áll rendelkezésünkre, csakhamar megnyugtatja a kedélyeket, írjuk fel tehát a boszorkányos egyszeregyet:

1x1=1	2x1= 2	3x1= 3	4x1= 4	5x1= 5
1x2=2	2x2= 4	8x2=10	4x2=12	5x2=14
1x8=3	2x3=10	3x3=13	4x8=20	5x3=23
1x4=4	2x4=12	3x4=20	4x4=24	5x4=32
1x5=5	2x5=14	3x5=23	4x5=32	5x5=41

Most összeadni, kivonni, szorozni, osztani fogunk úgy, mintha mitsem tudnánk a tízesrendszerről. Először tehát egy összeadást:

4825

5041

13410

Valahányszor két szám összege a hatot eléri, tízet kell gondolnunk. Tehát 1 meg 5 az 10, marad 1. Négy meg egy az öt meg kettő 11, marad egy. Nulla meg egy az egy meg három az négy. Öt meg négy az 18. Természetesen nem szabadna tizet, tizenegyet, tizenhármat mondani, hanem inkább hatot, hatonegyet, hatonhármat. A legnagyobb nehézség ezek szerint a nyelvben rejlik. Mihelyst szavunk van a fokszámok részére, minden számrendszer ugyanolyan könnyen használhatóvá válik, mint a tizesrendszer.

Nézzünk egy kivonást:

5201

—3544

1213

Szavakban: négyhez hogy tizenegy (hatonegy) legyen kell három, marad egy. Négy meg egy az öt, öthöz hogy tíz (hat) legyen kell egy, marad egy. Öt meg egy az tíz (hat) meg kettő az tizenkettő (hatonkettő), marad egy. Három meg egy az négy meg egy az öt.

Most az ígért szorzás, ehhez fog segítségül szolgálni az előbb felírt egyszeregy.

3425x31

15123

3425

155055

A szorzás próbáját tizesrendszerbe való átszámítással végezhetjük el.

3425 = 5x6°+2x6¹+4x6²+3x6³= 809

(hatosrendszer)    (tízesrendszer),

31 (hatosrendszer) = 1x6°+3x6¹ = 19 (tízesrendszer).

A tízesrendszerő szorzás a következő:

809x19

7281

15371

Ha helyesen számoltunk, továbbá, ha az az állításunk, hogy a hatosrendszerben az algoritmus ugyanaz mint a tízesben, akkor 15,371 (tizesrendszerben) ugyanannyi mint 155,055 (hatosrendszer), tehát sorokban felírva 1x10°+7x10¹ + 3x10²+ 5x10³+1x10¹=5x6⁰+5x6¹+0x6²+5x6³+5x6⁴+lx6⁵. Szerencsére és örömünkre fennáll a két sor megkövetelt egyenlősége, s erről mindenki meggyőződhet, így tehát már csak a hatosrendszer osztásával vagyunk adósak, de ezt azonnal pótoljuk. Bátrak vagyunk és nem félünk a nagy számoktól. Tehát:

2004013 : 425=2413 (hatosrendszerben)

3100

1041

2123

000

Az osztás ezek szerint, ahogy mondani szokás, kiment. Természetesen az osztásnál is folyton szem előtt kellett tartanunk, hogy hatosrendszerrel van dolgunk, így már annál az első becslésnél is, amellyel az osztás minden rendszerben kezdődik. Kezdésnél ugyanis, osztás előtt, feltesszük magunknak a kérdést: hányszor van meg az osztó az osztandóban, illetve az osztandó számcsoportjában. Esetünkben: hányszor foglaltatik a 425 a 2004-ben ? Tizesrendszerben néggyel kísérleteznék. Hatosrendszerben meg kell fontolnom, hogy 20 értéke tizesrendszerben 12, négyé viszont mindkettőben 4. Mivelhogy a 20 után ismét 0 következik, a 4 után pedig 2, ugyanaz a helyzet, mintha tizesrendszerben 120-at kellene 42-vel osztanom. Így tehát a kettest kell megpróbálnom. Az eredmény második jegyének meghatározásához 31 osztandó 4-gyel. 31 tizesrendszerben 19-et jelent, tehát négyet fogok próbaképpen felírni. Egyébként nemcsak használhatjuk, de használnunk is kell boszorkányos egyszeregyünket. (Ezzel feleslegessé válik, hogy minduntalan visszatérjünk a tizes-rendszerbe.)

Telhetetlenekké tettek eddigi eredményeink, s a számelmélet tudományának újdonsült tudósaiként még feltétlen bizonyságát is kívánjuk annak, hogy osztásunk helyes. Erre két módunk is van. Először, mint a szorzásnál tettük, visszahelyezhetnénk egész műveletünket a tizesrendszerbe, amelyben érthetőn biztosabbaknak érezzük magunkat. De ezúttal sokkal büszkébbek vagyunk, semhogy ezt a banális utat követnők. Mert algoritmusunkat még biztosabban markunkban szeretnénk tartani. Ezért így következtetünk : minden elemi iskolás tanuló, ha nem, bízik benne, hogy helyes az osztása, megcsinálja a próbáját azaz megszorozza az osztót a hányadossal és megnézi, vajon eredményül az osztandót kapja-e. Szkematikusan:

Osztandó: osztó=hányados,

Osztó X hányados=osztandó.

S minthogy, mint már említettük, a tizesrendszert már egyáltalán nem akarjuk segítségül igénybe venni és a hatosrendszer elemi iskolai tanulóinak tekintjük magunkat, szorozzuk össze (hatosrendszerben) az alábbi számokat:

Rendben van. A próba sikerült, ezek szerint helyesen kaptuk meg a hányadost. Ellenfelünk azonban körmünkre néz és következetlenséggel vádol. Ugyanis, felhívja figyelmünket, hogy nem a szkéma szerinti osztószor hányados hanem a hányadosszor osztó műveletet írtuk fel próbaként. Habár mindenki mellénk áll és vallja, hogy ez mindegy, mert hisz 4x5 ugyanazt az eredményt adja mint 5x4, mégis hálásak vagyunk ellenfelünknek, hogy alkalmat adott egy kis kitérésre.

Összeadás és szorzás úgynevezett építő műveletek. Összekapcsolnak, szaporítanak. Eredményük összetétel, szintézis. Innen szigorúan tudományos nevük : szintetikus, vagy röviden tétikus műveletek. Ezzel szemben a kivonás és az osztás felold, csökkent, lebont. Így ezek analitikus, röviden litikus műveletek. Világos, vagy óvatosabban szólván, valószínű, hogy lesz még az építő és bontó műveleteknek közös csoporttulajdonságuk is. De e helyütt egyáltalán nem óhajtunk mélyebbre menni. Ellenfelünk közbeszólását csupán annak bemutatására akarjuk felhasználni, hogy az összeadásnak és szorzásnak a kivonással és osztással szemben igen fontos csoporttulajdonsága van, amelyet mindenki ismer: alkatrészeinek, tagjainak sorrendje felcserélhető, a nélkül, hogy az eredmény megváltoznék. 5+7+4=7+5+4=4+5+7 stb. Ugyanígy 4x7x5=5x4x7=7x4x5 stb. Szabály: építő, tetikus műveleteknél érvényes az alkatrészek felcserélhetőségének elve (kommutatív műveletek). Feloldó műveleteknél, amelyek mellesleg megjegyezve, tudásunk mostani fokán mindenkor csak két tagból állanak, semmi esetre sem érvényes ez a. törvény. Ezek mintegy egyirányúak. Mert lényegesen más, hogy 5-ből vonok-e ki 4-et vagy 4-ből 5-öt. Éppígy más, hogy tizenkettőt osztok hárommal vagy hármat tizenkettővel. Megengedem, hogy ez a kitérés tudásunk mostani fokán természetes dolog fölöslegesen bőbeszédű taglalásának látszik, ezért már most rámutatok, hogy vannak további tetikus és litikus műveletek is, de azoknál a dolog korántsem ilyen egyszerű, azok tehát alaposabb vizsgálatra szorulnak.

De térjünk vissza számrendszereinkhez. A hatosrendszerrel elvégzett kísérleteink kíváncsivá tettek. Azt már elhisszük, hogy tízen aluli alapszámmal érvényes az algoritmus, az igaz kabbala, de még egyáltalán nincs bebizonyítva, hogy tíznél nagyobb alapszám is beválik helyértékrendszer alapszámaként. Azonban nem vághatunk neki vaktában a számok tengerének, mert nem volna gazdaságos például 50-et alapszámnak választani. Persze lehetséges volna. De 50 hatványai oly szédítően gyors iramban nőnek, hogy áttekintésünket teljesen elveszítenénk. S tudjuk azt is, hogy annyi számjegyre van szükségünk, ahány egységet alapszámunk tartalmaz. Hol vegyük a jeleket hozzá, ha nem akarunk napokat fordítani feltalálásukra és megtanulásukra?

Megelégszünk tehát azzal a feltétellel, hogy alapszámunk nagyobb legyen tíznél és jóravaló kabbalistákhoz méltón 13 lesz az alapszámunk. Mellékcélunk, hogy bemutassuk: alkalmas alapszám bármely úgynevezett törzsszám is, vagyis olyan szám, amely más egészszámmal nem osztható. Ehhez is fűzzünk egy megjegyzést. Dekadikus rendszerünk alapszámát (10), csak a 2 és az 5 osztja. 12-nek már 2, 3, 4 és 6 is osztója. Ezért már nem egyszer komolyan felvetették azt az ötletet, hogy hagyjuk el tizesrendszerünket és térjünk át a tizenkettesrendszerre. Pénz-, mérték- és súlyrendszerünk mérhetetlen hasznát látná, nem is szólván arról, hogy a nap beosztása (az óra számlapja) és a kör szögbeosztása könnyen egyesíthető a tizenkettesrendszerrel. Ellene főképpen természeti okok szólnak, ujjaink száma és egyéb testi adottságaink, amelyek nagyjából mindig a kettes és az ötös számokat kedvelik (szemek, fülek, karok, lábak, ujjak és lábujjak). Méterrendszerünk minden hozzáfűzött részével együtt tízes alapon függ össze a Eöld méreteivel, mert a francia forradalom óta a Föld negyed délkörének tízmilliomod részeként határozzák meg a métert. A többi érték, így a liter, a kilogramm stb. tizesrendszerrel kapcsolódik a méterhez. Végül pedig csillagászati véletlen, hogy egyik legfontosabb világállandó, az úgynevezett fénysebesség másodpercenként majdnem pontosan 800.000 kilométer. (Ha a métert a negyedmeridián tizenkettesrendszerben vett 10,000.000-d részeként definiálnánk, akkor a fény tizenkettesrendszerben írt 26-szor akkora utat tenne meg másodpercenként, azaz 260,000 "kilométert". Ez pedig lényegesen kevésbé «kerek» szám.)

Kevés tehát a remény, hogy belátható időn belül más számrendszert kelljen megtanulnunk. És így nem annyira gyakorlati, mint inkább elméleti okokból fogunk most még egy keveset tizenhármas számrendszerünkkel foglalkozni. Ismét felírjuk egymás alá összehasonlításul az első számokat, ezúttal harmincat, tizes és tizenhármasrendszerben.

Itt is felírhatnánk boszorkányos egyszeregyünket, benne 5x8 = 31 és 7x7=3A stb. volna, de ezt a szorgalmi feladatot és azt a felfedezést, hogy AxB=86, azoknak az olvasóinknak engedjük át, akik a számrendszerek tanulmányozásában mélyebben óhajtanak elmerülni.

De tizenhármasrendszerünket valahogyan igazolnunk is kell. Erre a célra szorzást választunk ki. És pedig a 92B és A7 számok szorzását, amit a tizenhármasrendszer madárnyelvén körülbelül úgy lehetne kimondani, hogy kilencszáz-huszonBészer Avanhét. Tehát:

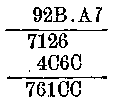
Szavakkal: A-szor B az 86 marad 8, A-szor 2 az 17 meg 8 az 22 marad 2. A-szor 9 az 60 meg 2 az 71. Továbbá: 7-szer B az 5C marad 5,7-szer 2 az 11 meg 5 az 16, marad 1. 7-szer 9 az 4B meg 1 az 40. Ezután az összeaadás. Egyesek helye : C. Második hely : 6 meg szintén C. Harmadik hely : C+2=ll marad 1. .Negyedik hely: 4+1=5 meg 1 az 6. Ötödik hely: 7. Tehát az eredmény 76,1CC.

De mivel nem akarunk túl sokat kínlódni, megkockáztatjuk a banalitást és a próbáját tizesrendszerben csináljuk meg. Mégpedig sorrá való felbontással.

92B (tizenhármasrendszer) = Bx13°+2x13¹+9x13²=11x1+2x13+9x169=

1558 (tizesrendszer)

A7 (tizenhármasrendszer) = 7x13°+Ax13¹=7x1 +10x13=137 (tizesrendszer).

Most végezzük el a tizesrendszerbeli szorzást:

1558x137

4674

10906

213446

A tizenhármasrendszerbeli szorzás eredménye 761CC. Szükségképpen ez ugyanannyi mint a tizesrendszerben 213446. Írjunk tehát tizesrendszerben, a hatványokat azonnal kiszámítva.

12x1+12x13+1x169+6x2197+7x28561=12+156+169+13,182+199,927=213,446.

Ezzel megkapjuk a várt eredményt és bebizonyítottuk, hogy tizenhármasrendszerben, tehát olyanban, amelynek alapszáma tíznél nagyobb, a helyértékrendszer számítási szabályai alkalmazhatók. Meg kell ugyan jegyeznem, hogy matematikus ilyen bizonyítást egyáltalán nem tekint érvényesnek. Eljárásunkat még a legjobb esetben is csak igazolásnak, verifikációnak nevezi. De mi egyelőre megelégszünk ilyen csekély értékű «bizonyítással» is, tekintve, hogy esetünkben ez veszélytelen és egyértelmű.

Most egyszerre a számok hegységének tetején állunk. A kapaszkodás fáradalma, a számok és számolások tüskés bozótja pillantásunkat eddig a földre szögezte. Most azonban, túl minden panaszon, túl a sok izzadságon és türelmen, körülnézhetünk a magasban. Mit látunk? Számtalan sok völgyet látunk és sejtünk, mindegyik hasonlít valamelyest a tizesrendszer völgyéhez, mégis különböznek tőle sokrétűségükben és kezdetük (6, 10, 13) méretében. Mindegyik a végtelenbe vezet, a határtalanba. Mindegyik helyet ad valamennyi természetes számnak. És mégis, minden völgyben más és más a számnövénykék színe és vastagsága...

Ne vigyük túlzásba hasonlatunkat. Elégedjünk meg ama képszerű gondolattal, hogy oly csúcson állunk, ahonnan valamennyi helyértéktípusú számrendszert áttekinthetjük. Minden ilyen rendszer egy-egy tévedhetetlen, önműködő algoritmus, gondolkodó- és számológép. Egyforma a rendszerek szerkezete: egyetlen alapszám; annyi számjel, a nullát beleértve, ahány egységet az alapszám tartalmaz ; helyérték, vagyis minden együttható, minden szám belsejében írt számjegy, az alapszám oly hatványával szorozva gondolandó, amilyen a helyét megilleti. Az egyesek helyét a rejtélyes nulladik, minden következő helyét eggyel-eggyel magasabb hatvány illeti meg. A kiszámított hatványokat fokszámnak hívjuk. Ha a rendszert gyakorlatban is használni óhajtjuk, az is szükséges, hogy legalább is az első fokszámoknak saját nevük legyen. Minden rendszerben vannak egy, két, három és többjegyű számok. Minden szám jegyeinek száma eggyel nagyobb, mint a legmagasabb helyértékű számához tartozó hatvány. (1268 például négyjegyű, legmagasabb értékű, ezres, helyén tehát harmadik hatvány fordul elő, mivel 1000 = 10x10x10=10³; hétjegyű számnál, például 2,586,938, a milliósok helyéhez tartozó hatvány a hatodik, mert 1,000,000= =10x10x10x10x10x10=10⁶ stb.) Továbbá minden helyértéken alapuló számrendszerben egyformák az alapműveletek : az összeadás, kivonás, szorzás és osztás szabályai.

Mielőtt még a számrendszerekre vonatkozó vizsgálódásainkból végső következtetéseinket levonnánk, meg kell említenünk, hogy ez az algoritmus, ez az igaz kabbala nemcsak a papíron végzett számításainknak nélkülözhetetlen kel léke. Csak az indiai helyértékrendszer alapján készíthetők a csodálatos mechanikus számológépek. Ezek regisztráló pénztárak és bérautók viteldíj mutatói alakjában láthatók leggyakrabban. Számelméleti kutatások alapján szerkesztették a tulajdonképpeni számológépeket is, azokat, amelyeket nagy bankok, könyvelőségek, műszaki irodák használnak. Bizony nem csodálatos, hogy az a nagy Leibniz alkotta az első számológépet 1674-ben Párizsban, aki az igazi kabbala elterjedésének is úttörője volt. Ez az első számológép már tartalmazta mindazokat az alkotórészeket, melyek a mai különféle rendszerű csodagépek alapjai.

De a helyesen megszerkesztett algoritmus automatikus működésének fogalmán kívül, — ennek jelentőségét mar mindnyájan ismerjük — fáradozásaink eredményeként olyan matematikai alapfogalmakat is tisztázni és rögzíteni akarunk, amelyek elsősorban tudományunk magasabb fokán lesznek rendkívül jelentősek : az általánosság fogalmát, az alakegyenlőségét és a formaállandóságét. Mivel nem akarunk matematikai filozófiával foglalkozni, ezeket a nagyon elvont fogalmakat is képszerűen vezetjük le eddigi kutatásainkból.

A tizesrendszerből indultunk ki, isteni eredetűnek tartottuk eleinte, de rövidesen észrevettük, hogy csak egy a számtalan lehetséges rendszer közül. Így bukkantunk a helyértékkel felírható számrendszerek általános alakjára. Ilyen rendszer számára, melyek alapszáma bármely tetszésszerinti szám lehet, általános szabályokat állítunk fel, ezek már nincsenek egy, különleges esethez kötve, hanem minden rendszerben érvényesek, tehát általánosak. Ezek szerint a rendszerek alakra egyformák. Tudományos néven ezt izomorfizmusnak hívják. A formaállandóság viszont azt jelenti, hogy bizonyos alakegyenlőség esetén szabályok egész sora nem változik meg, még ha valóságos megjelenési formájuk lényegesen eltér is egymástól. A tizesrendszer, a hatosrendszer, a tizenhármasrendszer és a többi sok más helyértéken alapuló számrendszer alakra egyenlő, izomorf. Ennek következtében a szorzás szabályai például valamennyiben azonosak. A hely-értékrendszerek szorzással szemben formatartók, más szóval invariánsak, mintegy érzéketlenek. A szorzásra nézve közömbös, hogy milyen rendszerben hajtjuk végre. Mindig ugyanazon az úton-módon történik és eredménye mindig ugyanaz. Ezért minden számológépet, elvének megváltoztatása nélkül, néhány alkotórészének kicserélésével át lehetne alakítani hatos vagy tizenhármas rendszerre. Engedelmesen szolgáltatnák a más számrendszerben felírt eredményeket.

De ne mélyedjünk el túlságosan vizsgálódásainkban. Ez a pontosság rovására menne, tekintve, hogy tárgyi tudásunk mértéke nem haladja meg egy kilencéves elemi iskolai tanulóét.

Kétségeink is támadtak. Eszünkbe jutott a diadika, a nagy Leibniz kettesrendszere és felfedezzük, hogy e rendszer egyszeregye egyetlen tételből áll, abból, hogy 1x1=1, tekintve, hogy a nullán és az 1-en kívül más számjegyet nem ismer. Diákok ezt az egyszeregyet mindenesetre nagyon csábítónak tartják. Minket annál inkább zavarba hoz. Hisz azt állítottuk, hogy minden rendszerben egyforma szabályok szerint lehet számolni. Hogyan szorozzak azonban, ha csak annyit tudok, hogy egyszer egy az egy?

Más kérdés is kínoz. Eddigi tudásunkkal meg akartuk határozni, hogy hány két-, három-, négy-, tízjegyű szám van valamely tetszésszerinti alapszámú rendszerben; de közben különféle akadályba ütköztünk.

Így tehát még kénytelen-kelletlen továbbra is egészszámokkal kell foglalkoznunk, mielőtt a «számok elméletének» hátat fordítanánk és az algebrával, tehát általános számokkal történő számolással kezdenénk foglalkozni. Ott fog minket az algebrai formák varázsa, az igazi, nagy kabbala megborzongatni.

NEGYEDIK FEJEZET

Szimbólumok és parancsok

Most, mikor már körülnéztünk a számok barátságtalan hegyének tetejéről, leszállunk az egyik völgybe, a mennyiségek és formák elvarázsolt országába. S olyan kérdés vizsgálatát kezdjük el, amely már régóta és egyre jobban kínoz bennünket. Hát nem több mint érthetetlen, tesszük fel magunkban a kérdést, hogy minden számrendszerben egyaránt képesek voltunk néhány számjellel a számok végtelenbe nyúló sorát felépíteni? Sőt nem arra utalt a nagy Leibniz, hogy ezt akkor is megtehetjük, ha csak a nullát és az egyet ismerjük?

Mostantól kezdve már majdnem kizárólag a gyermekkorunk óta jól ismert indiai-tizesrendszer völgyében fogunk vándorolni. Ezt jó előre megállapítjuk. De hogy tovább juthassunk, már mostan, utunk legelején felírom valamilyen táblára a következő bűvös jelet: 3! Mit jelent ez a számjegy a felkiáltójellel? Szinte kemény parancsnak látszik. De mit kíván tőlünk ? Mit kezdjek egyetlen számmal ? Széthasítsam, változtassam, nagyítsam, kicsinyítsem? Szerecsenek országába jutottam s az egyik vadember fejedelmi gesztussal dühös, tagolatlan hangot üvölt felém?

Egy kis türelmet kérek! — válaszolom. Két tervem is volt a bűvös jellel. Egyrészt bepillantást nyújtani a matematikai jelölésmódokba, másrészt elővenni ijesztő problémáink varázskulcsát, hogy már eleve kéznél legyen. A parancs természetesen nem csak 3! lehetett, 1! 5! 25! 273! 102077! éppen annyira lehetséges.

Azonban még mielőtt a felkiáltójellel jelölt parancs alaposabb tárgyalásához fognánk, lássuk előbb általában a matematikai parancsok módját és célját. Anélkül, hogy észrevettük volna, már ilyen parancsok egész sorozatának engedelmeskedtünk, mivel ehhez az engedelmességhez már az elemi iskolában hozzászoktunk. Megállapítottuk, hogy az egyes számjegyek és a belőlük összetett számok bizonyos csoportfogalmak jelei, jelképei, mondhatnánk szimbólumai. Beszéltünk továbbá rendszerről és bizonyos csodálatos számolási eljárásról, az algoritmusról. De ez a világ még rejt valamit: éppen a parancsokat! Ezeknek a feljegyzése és általános érthetősége képesít csupán arra, hogy a magukban álló számjegyeket rendszerbe foglaljuk és algoritmussá bővítsük. Mivel a matematikai műveletet operációnak nevezik, operációsparancsról és ennek jeléről, operációs szimbólumról is beszélhetünk. A parancsnak röviden «operátor» is lehetne a neve. Azonban a következők során megtartjuk egyszerű «parancs» kifejezésünket, de természetesen mindenkor matematikai parancsra, matematikai műveletek elvégzésére utasító felszólításra fogunk gondolni

Amint a katonaságnál eleinte nehezére esik az újoncnak, hogy a kaszárnyaudvaron vagy a gyakorlótéren egyetlen rövid vezényszó alapján bonyolult puskafogások egész sorát, legkevésbé sem egyszerű menet- és díszalakzatba fejlődést kell pontosan elvégeznie, úgy számúnkra is, akik a matematika újoncai vagyunk, a legnagyobb nehézség a «parancs» megértésében és pontos elvégzésében rejlik. Pedig ez a "matematikai fegyelem" rejti a matematikai készség kilenc tizedét.

Elhatároztuk, hogy a legegyszerűbb dolgokon kezdjük.

Először tehát a legegyszerűbb lépéseket és tisztelgési gyakorlatokat is parancsra fogjuk végezni.

A dolgok ilyen szövegezése meglepő lehet és rendíthetetlen ellenfelem megint felesleges bőbeszédűséggel gyanúsít. De nem tudok rajta segíteni. Mert feltett szándékom, hogy az integrál fogalmát éppen olyan érthetővé teszem, mint amilyen az összeadás jele. De ez a terv széleskörű előzetes matematikai tudás feltételezése nélkül csakis az én módszeremmel valósítható meg. Különben is, «parancsokról» már beszéltünk. Az összeadás jele is «parancs». Parancs az integrál jele is. Kissé bonyolultabb mint az összeadás jele, de lényegében nem más.

Ellenfelem befogja a fülét. Nehezményezi, hogy az integrált már most meg akarom magyarázni. Pedig csak a bátorságunkat akarom növelni. Mindenekfelett nem szándékozom az összeadáson lényegesen túlmenni; legalábbis az elvi nehézségek szemszögéből tekintve.

Megállapítjuk tehát, az összeadás parancs. 5+4=9. Mit jelentsen ez? Jelentése : «kedves barátom, végy öt egységet és tegyél hozzá, számlálj hozzá, további négyet". Kis szünet, amíg elkészül. Azután? Azután, az egyenlőség jelét tesszük utána, egy szimbólumot, amelynek pontosan a következő az értelme : "Alázatosan jelentem, a parancsot végrehajtottam". Nos, és? — kérdi a parancsoló. Felelet: «A parancs végrehajtása után a jobboldalon új jelképet látunk, neve : kilenc». «Jól van, végeztem!»

Tekintve, hogy gyengéd lelkeknek a katonai előadásmód valószínűleg nem igen tetszik, hagyjuk el a laktanya udvarát és beszéljünk elvontan. A kivonás is ilyenféle parancs, a szorzás és nemkülönben az osztás is. Mindnyájan tudjuk már, hogy matematikai parancsok végrehajtása nagyon bonyolult lehet. Mint például többjegyű számok osztása tizenhármas számrendszerben. Matematikai parancs az a tény is, hogy mindenkor egy bizonyos számrendszerben kell számolnunk. Természetesen parancs a hatványozás is.

Már megkockáztathatjuk azt az állítást, hogy a matematikai parancs fogalmának szemléltetésére igen jelentős demonstrációs és példaanyaggal rendelkezünk. Térjünk tehát vissza kiinduló pontunkra, ahhoz a jelhez, amely már külső megjelenésében — felkiáltó jel lévén — parancsra emlékeztetett.

Milyen vezényszót jelent tehát 3! a matematikában? Akik már értenek a dologhoz azt felelik, hogy három «fakultás»-áról vagy (nem teljesen helyes kifejezést használva) «faktoriális»-áról van szó. Helyes, ne mellőzzük teljesen a szakkifejezéseket. De a magunk kaszárnya-nyelvére is át akarjuk tenni azt a parancsot, amely ebben és csakis ebben a felkiáltójelben rejlik. Általában azt jelenti: «Vedd az egyet, szorozd meg kettővel, az eredményt hárommal, majd néggyel, mindezt öttel és így szorozz tovább mindaddig, míg végül az utolsó szorzó a felkiáltójel előtti szám nem lesz». Ha a felkiáltójel az egy mögött áll, nincsen további tennivalónk. Körülbelül ugyanúgy, ahogyan első hatványra sem kell emelnünk. De ne sokat magyarázgassunk, számítsuk ki inkább nagymerészen néhány számnak eme misztikus «fakultását».

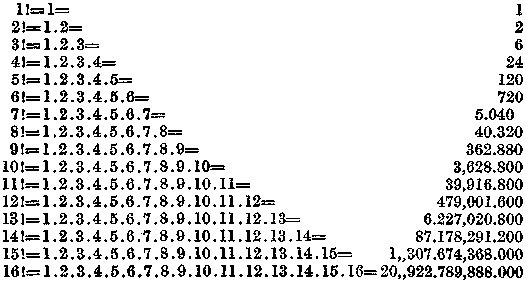
Látható, hogy parancsunk, a felkiáltójel hamarosan óriási eredményeket hoz létre. Ártatlanul, szinte alattomosan kezdődik az eredmények sorozata, fokozatosan növekedik, majd egészen hirtelen emelkedik és oly számokat ér el, amelyek messze meghaladják képzeletünket. Száznak a fakultása már gigantikus nagyságú számszörnyeteg. 158 számjeggyel lehet csak leírni.

Nem akarunk részletekbe bocsátkozni, de tisztán szemre is megállapíthatjuk, hogy a fakultás és a hatvány közt némi hasonlatosság van. Lényegbevágó különbség azonban, hogy amíg a hatványnál mindig ugyanazt a számot kell szorzóként alkalmaznunk, addig a fakultás egymás után következő tényezői fokozatosan növekszenek. Hatványozzunk összehasonlításul e helyen egy viszonylag kis számot, ezért említsük meg a sakktábláról szóló régi, ismert feladatot. A mese, erősen rövidítve, így szól: Bagdad egyik kalifája felszólítja matematikusát, hogy kívánjon magának valamit. Ez ártatlan arccal így szól: «Szerénytelen a kérésem, ó nagyhatalmú kalifa. Búza szemeket szeretnék jutalmul kapni. A következőképpen : annyi búzaszemet kapjak, ahány egy sakktábla utolsó mezejére kerül, ha az elsőn egyetlen szem fekszik és minden további mezőn kétszer annyi, mint ahány az előzőn volt». Nevet a kalifa és megígéri a kérés teljesítését. Szentül hiszi, hogy a hóbortos matematikus még egy egész kenyeret sem fog tudni sütni a búzából. De hamarosan eloszlanak kellemes illúziói. Tekintettel arra, hogy a búzaszemek száma 1x2=2, 2x2=4, 4x2=8, 8x2=16,16x2=82, 82x2=64, 64x2=128, 128x2=256, vagyis (1x2x2x2x2x2x2 ...) és így tovább a sakktábla utolsó mezejéig. A sakktáblán 64 mező van, tehát a szemek száma 2⁶³, minthogy az első mezőn csak egyetlen búzaszem volt. Ha kiszámítjuk, a következő számot kapjuk:

9,„223,372„036,854,775,808

Azzal szemléltethetjük ezt a számot, hogy a "sakktábla utolsó mezejére" kerülő búzamennyiség megtöltene egy 7x48 kilométer élhosszúságú kockát, ha feltételezzük, hogy a búza szemenkénti átlagos helyszükséglet 45x45 köbmilliméter. A fenti adat valóságosan elvégzett számolásból ered, amikor is 22.000 szem búza ment egy literre.

De kalifánk teverakományra is átszámíttatta ezt a búzatömeget. Ez a kép még szörnyűbb. Ha, a mi mértékrendszerünkben számolva, egy teve 140 kilogrammot bír el és mondjuk «libasorban» 5 méter helyre van szüksége, akkor a búzánkat vivő, 2,,303,539,469,744 tevéből álló karavánunk 11„517,697,348,720 méter, tehát több mint 11 1/2 millárd kilométer hosszú. Ez a karavánhossz azonban durván a Saturnus 8-szoros, vagy a Mars 50-szeres Naptávolságát jelenti.

Meg egy harmadik hasonlat: A föld búzatermése az 1927—1931. évek átlagában évi 1236 millió métermázsa volt, tehát szegény kalifánknak 2609 huszadik századbeli, traktorral és műtrágyával előállított búzatermést kellett volna előteremtenie, hogy a matematikusnak tett ígéretét megtarthassa.

A búzaszemek száma 19 számjeggyel írható le. Ebből talán sejtheti az olvasó, hogy mit jelent az a 158 jegyű szám, amely a 100! kiszámított értékét megadja.

ÖTÖDIK FEJEZET

Kombinatorika

Ártatlannak látszó, különféle matematikai «parancsok» következtében nagyranövő számok közé vezető kitérésünk után igyekezzünk tapogatódzva oda eljutni, ahol «fakultásokkal» számolunk : tehát arra a területre, ahol a felkiáltójeles számmal jelölt 1x2x3x4x5x6x7x8 stb. szorzat fogalmát használják. Ez a fogalom része a kombinatorika nevű algoritmusnak, tehát a tágabb értelemben vett kombinálási tudománynak. A «kombinálás» szó eléggé közkeletű ahhoz, hogy részletes magyarázgatásával ne kelljen sokat vesződnünk. Összeállítástudománynak, vagy az átrendezés tudományának is nevezhetnénk, de azt hiszem nyugodtan megmaradhatunk a kombinatorika elnevezésnél is.

Távol álljon tőlünk ismét a gondolat is, hogy definíciók és megállapítások sorozatát bocsássuk előre, noha, matematikai szempontból ez volna a helyes eljárás. Újoncok, vadócok vagyunk és tapasztalatokat gyűjtünk és azt fedezzük fel, ami érdekel bennünket. Azonban ellenfelünk kétségbeesett oldalpillantásának hatására annyit engedek álláspontomból, hogy ezennel ünnepélyesen kijelentem, hogy azért sohasem fogjuk a matematikát tapasztalati tudománynak tekinteni. A matematika, nagyjában így mondhatnánk, teljes egészében agyunk terméke, tapasztalatok nélkül is felépíthető és eredményeit tapasztalat sohasem fogja igazolni vagy megcáfolni. Erre csak logikai lépéseinek helyességét ellenőrző vizsgálat alkalmas. De mindez mellékes és csak a filozófiai érdeklődésű olvasóinknak szól; ezek pedig jegyezzék elő ennél a témánál az «a priori» és «apriorisztikus» szavakat.

Alkalmazzuk tehát, mit sem törődve ellenfelünkkel, az általunk már jól ismert matematikai anyagot. Vessük fel harmadszor is azt a kérdést, hogyan lehetséges tíz jellel a tizes számrendszerben a világ valamennyi számát felírni. Mindenki, aki csak ránéz a következő számokra: 123, 132, 213, 231, 312, 321, ha legalább valamelyes érzéke van a szavak mélyebb értelemhez, azt fogja mondani, hogy az egyes számjegyekből kombináltuk őket. Igaza van! A már tárgyalt rendszerek minden száma kombinatorikus úton származik a számjegyekből. Cserélgetjük a számjegyeket, a jelek váltogatásával állítjuk össze számainkat és így adunk az egyes számoknak más és más jelleget. Ne szóljunk itt a helyértékről. Minket csak az érdekel, hogy a <<számképek» külső alakjuk szerint miképpen csoportosíthatók. De ha mindent pontosan átgondolok, rájövök, hogy lényeges eltérések mutatkoznak a csoportosítás módszerében is. Tíznél kevesebb jegyű számok esetén a tíz jelből csak egyet-egyet, kettőt-kettőt és így tovább, legfeljebb kilencet használok fel egy csoporthoz. Ezen felül jogom van ugyanazt a jelet, mint pl. 1111 vagy 1212, 1112 esetén, többször is felhasználni. Tízjegyű számoknál már valamennyi számjegyet is használhatom és megelégedhetem egymásközti cserélgetésükkel is. Például 1234567890 vagy 1347658092. De létezik olyan tízjegyű szám is, amelyben a jegyek ismétlődnek. Ilyen pl. 1,000,000,000 vagy 2,322,234,777. Tíznél több jegyű számok esetén már elkerülhetetlen, hogy egyes jelek ne ismétlődjenek, tekintve, hogy nem használhatok huszonötféle jelet, ha csak tíz létezik.

Darázsfészekbe nyúltunk. És azt hiszem, első lépésünk inkább zavarba hozott mint felvilágosított. Miként foghatjuk meg ezt a végtelenbe terpeszkedő számkáoszt bármilyen algoritmussal is? Mit használ a «parancs», ha az ember feje kóvályog? A «kísérlet» sem segít. Az elemek számának legkisebb növekedése — hamar meggyőződhetünk róla — a lehetőségek olyan számához vezet, hogy éjjel-nappal «kombinálva» is csak naprendszerek életkorával mérhető idő alatt jutnánk a végére. Bűvészinas lett az első "algoritmusunk" (a számrendszer) és úgy látszik, a maga hordta vízben merül el. Tehát mégis «parancsot»!

Igaz kabbalát csak kabbala győzhet le. Varázsszavak, bűvös jelek hatását csak varázsige semlegesítheti, teheti ártalmatlanná.

Kezdjük tehát azzal, hogy a kombinatorikát kombináljuk, az ördögöt Belzebubbal űzzük el. De hogy szakszerűségünket el ne veszítsük, a kombinatorika e kombinatorikáját, ezt a másodfokú kombinatorikát példákba bujtatjuk. De végül majd megvizsgáljuk, kimerítettünk-e minden lehetőséget és felállítjuk a kombinatorika zárt rendszerét is.

HATODIK FEJEZET

Permutációk

A sajnos, oly régmúlt idők valamely tisztes famíliája tizennégy tagú: apa, anya és tizenkét pompás, egészséges gyermek. Békésen ülnek együtt ebédjüknél. Egyszerre egyik fiú hangosan kezd panaszkodni. Azt panaszolja, hogy a levesből mindig csak a maradék jut neki, mert nagyon kedvezőtlen a helye az asztalnál. A család békés természetű, iparkodnak az ellentéteket kölcsönösen kiegyenlíteni. Rövidesen elhatározzák, hogy minden nap más sorrendben fognak asztalhoz ülni, mivelhogy a szobalánytól igazán nem kívánható, hogy minden nap más úton menjen az asztal körül. Beszélgetni kezdenek a történtekről és hamarosan megkísérlik meghatározni azt az időt, amely minden lehetséges sorrendváltozáshoz szükséges. "Néhány napba bizonyára beletelik" véli az egyik fiú. "Mondjunk inkább néhány hetet", vág közbe az egyik leány fölényesen. Végül is egy évben egyeznek meg. "Képlet van erre" szól most közbe a legidősebb fiú. "Nos, a matematika minek nevezi esetünket?" kérdi évődve az apa. A legidősebb néhány pillanatig habozik. Végül így szól: "Az asztal melletti ülésrendről lévén szó, nem közömbös, hogy Éva ül Alfonz után vagy Alfonz Éva után. Ez két különböző eset. Csoportokat sem alakítunk. Mindnyájan, mind a tizennégyen, minden alkalommal más sorrendben ülünk. Ugyanaz az eset, mintha tizennégy tárgyat, — tizennégy elemet mond a matematika — akarnék egymásután minden lehetséges sorrendben elhelyezni. A sorrend ilyen változtatását permutációnak nevezik. Számukat az elemek számának fakultása adja meg. Esetünkben tizennégy és utána felkiáltójel. Tizennégy fakultása!"

Az apa elégedetten bólint. A leves és a hús közt papírt és ceruzát hoznak és az idősebb gyerekek vérbe borult fejjel számolnak. Mennyi is lehet az a bűvös 14! Az eredmény ijesztő! Ennyi: 87,178,291,200. Mihez fogjanak e sok milliárd lehetőséggel? Mennyi idő kell hozzá? 365 napja van az évnek, osszuk el tehát 365-tel. Újabb számolás. Alfonz, a gyorsszámoló már mondja is: "238,844,633 az eredmény!" "Tudod mit jelent ez" kiált fel az egyik fiú, a család filozófusa, egészen elszörnyedve. "Azt jelenti, hogy közel 239 millió évre van szükségünk, hogy a lehetőségeket kimerítsük. Több mint 119 millió évre, ha naponta kétszer, s majd 60 millióra ha reggelinél, ebédnél, uzsonnánál és vacsoránál is változtatunk az ülésrenden". "És én meghalok, mielőtt még csak egyszer is jó levest kapnék" panaszkodik a kicsi.

Példánkon egyformán látszik az elcserélési lehetőségek sokfélesége, a "fakultás" parancs démoni hatása és a kombinatorikának egyik, első lehetséges fajtája. Ezzel ismét van "anyagunk, rendszeres feldolgozásra".

De még előbb az olvasó megnyugtatására: tisztes famíliánk megriad a kombinatorika által szolgáltatott eredménytől s a legifjabb panaszának megszüntetésére lényegesen egyszerűbb megoldásra jutott. A szobalány parancsot kapott, hogy ezentúl mindig ugyanannál a széknél kell a kínálást kezdenie, tekintet nélkül arra, ki ül ott. A család pedig, naponta egy székkel «odábbült», még pedig az óramutató járása irányában. Egymásközt, szomszédság tekintetében, az ülésrend változatlan maradt. De az asztalhoz viszonyítva napról napra változott. Ezáltal mindenki, minden két hétben egyszer, elsőnek kapott levest.

Matematikai szempontból itt is tizennégy különböző permutációval van dolgunk. Írjunk fel közülük néhányat:

1, 2, 8, 4, 6, 6, 7, 8, 9, 10, 11, 12, 18, 14 (első nap)

2, 3, 1,5, 6,7,8, 9,10, 11,12,13,14, 1 (második nap)

3,4,5,6,7,8,9,10,11,12,13,14, 1, 2 (harmadik nap)

és így tovább

14,1,2,3,4,5,6,7,8, 9,10,11,12,13 (tizennegyedik nap)

1,2,3,4,5, 6,7,8,9,10,11,12,13,14 (tizenötödik nap)

De az így felírt 14 esetet (az első és a tizenötödik ugyanis azonos) más elv, az úgynevezett ciklus felcserélés elve alapján mesterségesen választottuk ki a permutációk lehetséges 87,178,291,200 esete közül, azáltal, hogy mellékesen az egymásközti sorrend változatlanságát is kikötöttük.

Fenti példánkban a cserélendő ülőhelyeket számokkal jelöltük meg. Ábécé rendben vett betűkkel is lehetne őket jelölni. Természetesen ilyen számozás egyáltalán nem jelent nagyság szerinti rangsorolást, amint nem jelent semmi ilyet a színházi széksor üléseinek számozása sem. Azokat a dolgokat, amelyeket cserélgetnünk kell, színekkel, nevekkel, bármiféle ismertető jellel is megjelölhetném. Éppen ezért nevezik eme teljesen egyenértékű dolgok megkülönböztető jeleit indexeknek. Számok vagy betűk ilyen, csupán sorrendet jelölő felhasználási módja különösen Leibniz működése óta játszik, mindinkább jelentős szerepet a matematikában. Most megkíséreljük, hogy megmagyarázzunk magunknak valamit, ami igazán nehezen érhető. Leghatározottabban állítottuk, hogy dolgaink egyenértékűek, a számok és indexek semmiesetre sem jelentenek nagyságot. Mégis, egészen nyugodtan beszélnek arról, hogy a kettessel jelölt dolog «magasabb» vagy «magasabb rendű», mint az egyessel jelölt. Helyesen azt kellene mondani: a 2. jelű magasabb indexű, mint az 1. jelű. Egyébként az 1. jelű és a 2. jelű teljesen egyformák. (Elképzelhető ugyan, hogy a dolgok nagysága különböző, csupán nem törődöm vele. Engem csak az érdekel, hogy valamilyen dolog egység jellegű.)

Ismét valami kabbalaszerű dologról van szó. Még pedig a sorrend kabbalájáról, illetve a mellérendelés kabbalájáról. Egyszerűen nem tudnék beszélni, nem tudnék írni, ha nem szabadna az indexeket valamilyen rendszer alapján nagyságszerint rendeznem. Az ábécé korrektebb és talán kevésbé kétértelmű, mint a számindexekkel való jelölés, hisz az utóbbiak akaratlanul is magukkal hurcolják mérték jelenésüket. A d betű magasabb helyen áll az ábécében, mint a b. Így a d jelű dolog rendje kombinációs szempontból magasabb, mint a b jelűé. (Az ilyen sorrendet "lexikográfikus sorrendnek" is szokták nevezni. (Olyan mint egy lexikon!))

A "helyérték" ilyenértelmű meghatározásából magától adódik a kombinatorikában nélkülözhetetlen és alapvető fontosságú «helyes sorrend» fogalma. Helyes sorrend például, ha következőképpen képezek permutációkat:

abc, acb, bac, bca, cab, cba, vagy ugyanez számokkal

123, 132, 213, 231, 312, 321.

Ha tehát ily módon haladunk, vagyis a «legalacsonyabb» elem addig marad a helyén, ameddig csak egyáltalán lehetséges, akkor "helyes sorrendben" emelkedünk a "legalacsonyabb" permutációtól a «legmagasabbhoz», egyetlen permutáció sem maradhat ki és fáradozásaink jutalmául végül az első permutáció fordítottját kapjuk. Míg az első permutációban magasabb elem sohasem előzött meg alacsonyabbat, addig az utolsóban alacsonyabb elem mindenkor csak magasabb után következhet. Nem akarok zavart okozni, de elhallgatni sem tudom, hogy a permutációkat valódi számoknak olvasva a legalacsonyabb permutáció adja a legkisebb

számot, a legmagasabb a legnagyobbat. (123.....321).

Közben vannak, helyes sorrendben, mindazok, amelyeket csupán az 1, 2, 3 számjegyekkel le lehet írni.

De a legutóbbi összefüggést feltétlenül el kell felejtenünk és visszatérünk méretmentes indexeinkhez. 123 ugyanannyit jelent tehát számunkra, mint 321 vagy 231, tehát a választott három index egy-egy permutációját.

Most azt a problémát is meg fogjuk oldani, hogy titokzatos «parancsunk», «fakultásunk», a 3 a felkiáltójellel miért adja meg olyan pontosan a lehetséges permutációk számát. Először "a rendszer épségben tartása kedvéért" egy logikai értelmetlenséget fogunk állítani. Hasonlóval már a hatványozásnál, még pedig a nulladik és első hatványnál találkoztunk. Azt akarjuk tudni, mekkora a permutációk száma, ha csak egy elemünk van. Pontosabban : "addig cserélgess egy elemet, helyes sorrendben, amíg csak valamennyi lehetőséget ki nem merítetted".

Kellő megfontolás után az értelmetlenségnek matematikai fogalmazást adunk és ezzel újabb, talán még nagyobb értelmetlenséggel helyettesítjük. Büszkén felírjuk : a permutációk száma 1! (Egy fakultása.) Vagy szavakban : úgy kapjuk meg az eredményt, ha egyet, eggyel kezdve mindaddig szorozzuk az egymásután következő számokkal, míg végre utolsó szorzóként az egyhez jutunk! Nem lehet kétséges, hogy ily módon mást, mint egyet, nem kaphatunk eredményül.

Logikai kitérésünk után számoljunk óvatosan tovább. Mi történik két elem esetén ? Írjuk fel helyes sorrendben:

ab ba

Kétségtelen: valamennyi permutációt felírtuk, a legalacsonyabbtól a legmagasabbig. Most pedig beretva éles okoskodással haladjunk, hogy megtaláljuk az összefüggést az állítás formájában már ismert képlettel. Mit is tettünk tulajdonképpen? Az a elemet addig tartottuk helyén, ameddig csak lehetett és közben a b-t permutáltuk. Mihelyt készen voltunk, a b került első helyre, és az a-t permutáltuk. Tehát két esetben kellett mindkétszer egy elemet permutálnunk. Egy elemnek azonban csak egy permutációja van, két elemnek ily módon 1x2, vagyis írásmódunk szerint 2!, azaz kettő fakultása, ami kettővel egyenlő.

Három elemnél:

abc    bac    cab

acb    bca    cba

Ha újból alkalmazzuk módszerünket, látjuk, hogy háromszor tartottuk a rendelkezésünkre álló mindenkori első elemet lehető legtovább helyén és közben két másikat permutáltunk. Mivelhogy két elem permutációinak a száma 1x2, ezt most hárommal kell még megszoroznunk. Tehát három elemnél a permutációk száma 1x2x8, azaz 8!, három fakultása számszerűen 6. Négy elem esetén a helyzet a következő :

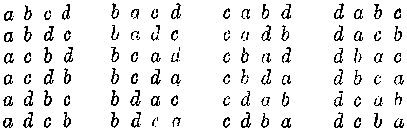
Nem ismételjük most már az egész eljárást. Röviden : a mindenkori első elemet addig tartottuk helyén, amíg a többi bárom permutálásával elkészültünk. De mert négy elemem van, vagyis négy foglalhatja el az első helyet, a bárom elem permutációinak a számát néggyel meg kell szoroznom. 4-szer 1x2x8, vagyis 1x2x8x4 tehát 4!, négy fakultása, ez pedig 24.

Így továbbhaladva látjuk, hogy különböző indexű elemekből alkotott permutációk számát megadja az elemek száma felkiáltójellel. Tehát 10 elemnek 10!, 75 elemnek 75!, 8124 elemnek 8124! permutációja lehetséges és így tovább a végtelenségig,

Megeshet, hogy nemcsak különböző elemek vagy indexek szerepelnek, hanem néhány egyenlő is van köztük. Durván: két almát, három barackot és egy szem cseresznyét cserélgessek, hogy e gyümölcsök összes lehetséges csoportosítása keletkezzék, de természetesen arra nem kell ügyelnem, hogy mikor veszem az 1. számú és mikor a 2. számú barackot. Ez azt jelenti, hogy a 2. számú alma, 1. számú alma, 2. számú barack, cseresznye, 8. számú barack, 1. számú barack sorrend és például 1. számú alma, 2. számú alma, 1. számú barack, cseresznye, 3. számú barack, 2. számú barack közt semmi különbség sincs. Egyszerűség kedvéért jelöljük az almákat a betűvel, a barackokat b-vel, a cseresznyét c-vel, akkor «helyes sorrendbem az első permutáció az

a a b b b c, és az utolsó c b b b a a.

Túlságosan sok időt venne igénybe, hogy módszerünkkel ilyen, "ismétléses permutációnak" nevezett esetekre a permutációk számát levezessük. Kérem tehát, higgyék el nekem úgy is a képletet, ha csak egyszerűen felírom. Esetünkben így hangzik : Az összes permutáció száma, tehát 6!, elosztandó az ismétlődő elemek fakultásának szorzatával. 6! tehát 2!, 3! és 1! szorzatával osztandó. Vagyis, ha ezt tört alakjában írjuk:

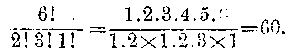
Gyümölcseinket tehát hatvan különböző csoportosításban helyezhetem el. Élénkebb matematikai fantáziájú olvasóim számára megjegyzem, hogy ez utóbbi képlet az általánosabb. Mert minden permutációnál feltehetem a kérdést, hogy hányszor szerepelnek az egyes elemek. És mondjuk öt különböző elem permutálásánál bízvást írhatom : a permutációk száma

minthogy minden elem csak egyszer szerepel.

Látjuk, az eredmény helyes. Első képletünk ezek szerint az általánosabb, másodiknak csak különleges (speciális) esete:

Permutációkra, vonatkozó vizsgálataink befejezéséül még egy példa. Hány permutációja van az a b b b b c elemeknek? Természetesen.

Jószemű olvasó bizonyára észreveszi, hogy ha a képletben eltekintek a felkiáltójelektől, akkor a törtvonal alatt és felett a számok összege szükségképpen azonos ; ez természetes is, hiszen először valamennyi elem számának fakultását írtam számlálónak, majd pedig az egyes alcsoportok elemszámának fakultását nevezőnek.

Sok mindent lehetne még a permutációkról elmondani. A problémáknak még egész sorát tárgyalhatnánk. De tekintve, hogy a permutáció általános matematikai szempontból éppen olyan kevéssé tekinthető a kombinációs módok legfontosabb fajtájának, mint ahogy nem az a mi különleges szempontjainkból sem, végezetül még csak megállapítjuk, hogy a permutációkban mindenkor valamennyi rendelkezésre álló elem szerepel, ezeknek az elemeknek sorrendjét változtatjuk és ez a sorrend mértékadó annak elbírálásánál, hogy két permutáció azonos-e vagy sem. Ha a sorrendtől eltekintenék és csak az összetételt venném figyelembe, akkor egy csoporton belül csak egy eset volna lehetséges. A permutálás tehát nem egyéb, mint elemek sorrendjének változtatása, elemek cserélgetése.

HETEDIK FEJEZET