Capítulo 4
CABOS SUELTOS
Voy a dividir esta conferencia en dos partes. En primer lugar voy a hablar de problemas asociados con la propia teoría de la electrodinámica cuántica, suponiendo que todo lo que existe en el mundo son electrones y fotones. Luego hablaré sobre la relación de la electrodinámica cuántica con el resto de la física.
La característica más chocante de la teoría de la electrodinámica cuántica es el loco marco de las amplitudes ¡qué Vds. pueden pensar que indica problemas de algún tipo! Sin embargo, los físicos han estado jugando con amplitudes desde hace más de cincuenta años y han terminado acostumbrándose a ellas. Además, todas las nuevas partículas y los nuevos fenómenos que somos capaces de obtener encajan perfectamente con lo que se puede deducir de ese marco de amplitudes, en el que la probabilidad de un suceso es el cuadrado de una flecha final cuya longitud viene determinada por la combinación de flechas en formas divertidas (con interferencias y cosas por el estilo). Por tanto, este marco de amplitudes no presenta ninguna duda desde el punto de vista experimental: puede Vd. tener todas las preocupaciones filosóficas que quiera en lo que se refiere al significado de las amplitudes (si, de hecho, significan algo) pero como la física es una ciencia experimental y el marco concuerda con los experimentos, esto es suficiente para nosotros por el momento.
Existe un conjunto de problemas asociados con la teoría de la electrodinámica cuántica que tiene que ver con la mejora del método de cálculo de la suma de todas las flechitas —técnicas diversas de las que se dispone en circunstancias diferentes— y que llevan tres o cuatro años el dominarlas a los estudiantes graduados. Puesto que son problemas técnicos, no voy a discutirlos aquí. Es sólo una cuestión de mejorar continuamente las técnicas para analizar lo que la teoría tiene realmente que decir en circunstancias diferentes.
Pero existe un problema adicional característico de la propia teoría de la electrodinámica cuántica, que llevó veinte años resolverlo. Está relacionado con los electrones y fotones idealizados y los números n y j.
Si los electrones fuesen ideales y se moviesen de un punto a otro del espacio-tiempo, sólo por el camino directo (mostrado a la izquierda en la Fig. 77) no existiría problema: n sería simplemente la masa de un electrón (que podemos determinar por observación) y j simplemente su «carga» (la amplitud de acoplamiento de un electrón y un fotón). También puede ser determinada experimentalmente.

FIGURA 77. Cuando calculamos la amplitud de que un electrón vaya de un punto a otro del espacio-tiempo, utilizamos la fórmula E(A a B) para el camino directo. (Luego hacemos «correcciones» que incluyen uno o más fotones emitiéndose y absorbiéndose). E(A a B) depende de (X2 − X1), (T2 − T1) y n, un número que introducimos en las fórmulas para que la respuesta fuese la correcta. El número n se denomina la «masa en reposo» de un electrón «ideal», y no puede ser medida experimentalmente porque la masa en reposo de un electrón real, m, incluye todas las «correcciones». Existía una cierta dificultad para calcular el n que debía de utilizarse en E(A a B), y llevó veinte años el remontarla.
Pero no existen esos electrones ideales. La masa que observamos en el laboratorio es la de un electrón real, que emite y absorbe sus propios fotones de vez en cuando, y que por tanto depende de la amplitud de acoplamiento, j. Y la carga que observamos está entre la de un electrón real y un fotón real —que puede formar un par electrón-positrón de vez en cuando—, dependiendo por consiguiente de E(A a B), que involucra a n (ver Fig. 78). Puesto que la masa y carga de un electrón se ven afectadas por estas y otras alternativas, la masa experimental medida, m, y la carga experimentalmente medida, e, del electrón son diferentes de los números que usamos en nuestros cálculos, n y j.

FIGURA 78. La amplitud experimental de acoplamiento entre el electrón y el fotón, un número misterioso, e, es un número determinado experimentalmente que incluye todas las «correcciones» para un fotón yendo de un punto a otro del espacio-tiempo, dos de las cuales se muestran aquí. Cuando hacemos los cálculos, necesitamos un número, j, que no incluye estas correcciones, sino solamente la del fotón yendo directamente de un punto a otro. Existe una dificultad para calcular este valor de j que es análoga a la existente para calcular el valor de n.
Si existiese una relación matemática definida entre n y j por un lado, y m y e por otro, tampoco existiría problema: simplemente calcularíamos los valores de n y j necesarios para empezar, a fin de terminar con los valores observados, m y e. (Si nuestros cálculos no concordasen con m y e, bailaríamos los valores iniciales de n y j hasta que lo hiciesen).
Veamos cómo calculamos m realmente. Escribimos una serie de términos que son análogos a la serie que vimos para el momento magnético del electrón: el primer término no tiene acoplamiento —sólo E(A a B)— y representa un electrón ideal viajando directamente de un punto a otro del espacio-tiempo. El segundo término tiene dos acoplamientos y representa un fotón que es emitido y absorbido. Luego viene el término con cuatro, seis y ocho acoplamientos y así sucesivamente (algunas de estas «correcciones» se muestran en la Fig. 77).
Cuando calculemos los términos con acoplamientos, debemos considerar (como siempre) todos los posibles puntos en donde los acoplamientos pueden tener lugar, incluido el caso en el que los dos puntos del acoplamiento se superponen —con distancia cero entre ellos—. El problema es que cuando intentamos calcular todas las situaciones hasta la de distancia cero, la ecuación explota ante nosotros y da respuestas sin sentido —cosas como infinito—. Esto originó muchas molestias cuando la teoría de la electrodinámica cuántica apareció por primera vez. ¡La gente obtenía infinito para cada problema que intentaba calcular! (Uno debería descender hasta la distancia cero a fin de ser matemáticamente consistente, pero aquí es donde ni n ni j tienen ningún sentido; y donde está el problema).
Bien, en lugar de incluir todos los posibles puntos de acoplamiento hasta la distancia cero, si se detienen los cálculos cuando la distancia entre los puntos de acoplamiento es muy pequeña —digamos, 10−16 cm— existen entonces unos valores definidos para n y j que se pueden usar de manera que la masa calculada coincida con la masa m observada en los experimentos y la carga calculada concuerde con la carga observada, e. Pero, aquí está la trampa: si alguien más hace los cálculos y los detiene a distancia diferente —digamos 10−40 cm—, ¡los valores de n y j que precisa para obtener los mismos valores de m y e son diferentes!
Veinte años después, en 1949, Hans Bethe y Victor Weisskopf notaron algo: si dos personas que paraban los cálculos a distancias diferentes para determinar n y j a partir de los mismos m y e, calculaban luego la respuesta a otro problema —cada uno utilizando los valores apropiados pero diferentes de n y j—, cuando incluían todas las flechas de todos los términos ¡sus respuestas a este otro problema eran casi idénticas! De hecho, cuanto más se aproximaban a la distancia cero en los cálculos de n y j, ¡mejor concordaban las respuestas finales para los otros problemas! Schwinger, Tomonaga y yo mismo inventamos, de manera independiente, formas de hacer cálculos definidos para confirmar que esto era verdad (obtuvimos premios por esto). ¡La gente pudo finalmente calcular con la teoría de la electrodinámica cuántica!
Por consiguiente parece que las únicas cosas que dependen de las pequeñas distancias entre los puntos de acoplamiento son los valores de n y j —números teóricos que no son observables directamente de ninguna manera—; todo lo demás, lo que puede ser observado, parece no verse afectado.
El juego de capas que utilizamos para encontrar n y j se denomina técnicamente «renormalización». Pero independientemente de lo inteligente que sea la palabra, es lo que yo llamaría ¡un proceso de profundización! El haber tenido que recurrir a tal malabarismo nos ha impedido demostrar que la teoría de la electrodinámica cuántica es matemáticamente autoconsistente. Es sorprendente que todavía no se haya podido demostrar de una manera u otra que la teoría es autoconsistente; sospecho que la renormalización no sea legítima desde el punto de vista matemático. Lo que es cierto es que no tenemos una buena forma matemática de describir la electrodinámica cuántica: semejante montón de palabras para describir la relación entre n y j y m y e no son buenas matemáticas[23].
Existe un problema más profundo y bonito asociado a la constante de acoplamiento experimental, e —la amplitud de que un electrón real emita o absorba un fotón real—. Es un número sencillo cuyo valor, próximo a −0,08542455, ha sido determinado experimentalmente. (Mis amigos físicos no reconocerán este número porque prefieren recordar la inversa de su cuadrado: aproximadamente 137,03597 con una incertidumbre de 2 en la última cifra decimal. Esta constante ha sido un misterio desde su descubrimiento, hace más de cincuenta años, y todos los buenos físicos teóricos colocan este número en su pizarra y se preocupan por él).
A Vds. les gustaría saber inmediatamente de dónde sale este número de acoplamiento: ¿está relacionado con π, o quizá con la base de los logaritmos neperianos? Nadie lo sabe. Es uno de los condenados misterios más grandes de la física: un número mágico que aparece sin que el hombre entienda cómo. Podrían decir que «la mano de Dios» escribió ese número, y que «nosotros no sabemos cómo cogió su lápiz». Sabemos al son de qué música bailar para medir experimentalmente con gran precisión este número, pero no sabemos el son para obtener este número en un computador —¡sin introducirlo en secreto!
Una buena teoría diría que e es la raíz cuadrada de 3 dividida por 2pi cuadrado, o algo similar. De vez en cuando, se han hecho sugerencias acerca de qué era e, pero ninguna ha resultado útil. Primero, Arthur Eddington demostró, por pura lógica, que el número que les gustaba a los físicos era exactamente 136, el valor experimental de la época. Luego, cuando experimentos más precisos demostraron que el número estaba más cercano a 137, Eddington descubrió un ligero error en su anterior razonamiento y mostró, de nuevo por pura lógica, ¡qué el número tenía que ser el entero 137! De vez en cuando, alguien advertía que una determinada combinación de π y e (la base del logaritmo neperiano) y doses y cincos producía la misteriosa constante de acoplamiento, pero es un hecho no apreciado en su totalidad por la gente que juega con la aritmética que es sorprendente la gran cantidad de números que se pueden obtener a partir de píes y ees y similares. Por tanto, a lo largo de la historia de la física moderna han aparecido artículo tras artículo de personas que han obtenido e con varias cifras decimales para que la siguiente ronda de experimentos mejorados produjese un valor en desacuerdo con él.
Pero aunque hoy tenemos que recurrir a un proceso de profundización para calcular j, es posible que, algún día, se encuentre una conexión matemáticamente válida entre j y e. En este caso sin duda que aparecerían otro montón de artículos que nos dirían cómo calcular j «con nuestras propias manos» por así decirlo, proponiendo que j es 1 dividido por 4 × pi o algo similar.
Esto muestra todos los problemas asociados con la electrodinámica cuántica.
Cuando planeé estas conferencias, intenté concentrarme sólo en la parte de la física que conocemos muy bien —describirla al completo y no decir, nada más—. Pero ahora que hemos llegado hasta aquí y siendo un profesor (lo que significa tener la costumbre de no ser capaz de dejar de hablar a la hora debida), no puedo resistir el contarles algo del resto de la física.
Primero, debo decirles inmediatamente que ninguna de las partes del resto del la física ha sido tan comprobada como la electrodinámica: algunas de las cosas que voy a decirles son buenas suposiciones, algunas otras, teorías parcialmente elaboradas y otras, pura especulación. Por lo tanto, esta presentación va a parecer algo así como un relativo lío, y comparada con las otras conferencias será incompleta y falta de muchos detalles. Sin embargo, ocurre que la estructura de la teoría de la QED sirve como base excelente para la descripción de otros fenómenos del resto de la física.
Comenzaré hablando de protones y neutrones, lo que constituye el núcleo de los átomos. Cuando se descubrieron por vez primera los protones y neutrones se pensó que eran partículas sencillas, pero pronto se evidenció que no eran sencillas —en el sentido de que la amplitud, para ir de un punto a otro podía explicarse por la fórmula E(A a B), pero con un número diferente para n en ella—. Por ejemplo, el protón tiene un momento magnético que si se calcula de la misma manera que para el electrón, debería aproximarse a 1. Pero de hecho, experimentalmente resulta un valor completamente loco ¡−2,79! En consecuencia, se vio pronto que algo ocurría dentro del protón que no se tenía en cuenta en las ecuaciones de la electrodinámica cuántica. Y el neutrón, que no debería tener interacción magnética si fuese realmente neutro, ¡tiene un momento magnético de aproximadamente −1,93! Por tanto, se sabía desde hacía bastante tiempo que algo raro ocurría también dentro del neutrón.
Existía también el problema de qué mantiene a los neutrones y protones juntos dentro del núcleo. Se apreció en seguida que no podía ser debido al intercambio de fotones, porque las fuerzas que mantenían unido el núcleo eran mucho más fuertes —la energía requerida para romper un núcleo es mucho mayor que la que se requiere para extraer un electrón de un átomo, en una proporción análoga al mucho más elevado poder de destrucción de la bomba atómica frente al de la dinamita—: la explosión de la dinamita es una redistribución de la disposición de los electrones, mientras que la explosión de una bomba atómica es una redistribución de la disposición de protones y neutrones.
Para descubrir algo más sobre lo que mantiene unido a los núcleos, se realizaron muchos experimentos en los que se hacía incidir, sobre los núcleos, protones con energías cada vez más elevadas. Se esperaba que sólo se obtendrían protones y neutrones. Pero cuando la energía fue lo suficientemente elevada, aparecieron nuevas partículas. Primero fueron los piones, luego las landas, y sigmas, y ros, y luego agotaron el alfabeto. Después aparecieron partículas con números (sus masas), tales como sigma 1190 y sigma 1386. Pronto se hizo evidente que el número de partículas en el mundo no tenía fin y dependía de la cantidad de energía empleada para desintegrar el núcleo. Existen en la actualidad más de cuatrocientas partículas. No podemos aceptar cuatrocientas partículas ¡es demasiado complicado![24]
Grandes inventores como Murray Gell-Mann casi se vuelven locos tratando de descubrir las leyes de comportamiento de estas partículas, y a principios de los setenta aparecieron con la teoría cuántica de las interacciones fuertes (o «cromodinámica cuántica»), cuyos actores principales eran las partículas denominadas «quarks». Todas las partículas compuestas de quarks se dividen en dos clases: algunas, como el protón y el neutrón, están formadas por tres quarks (y tienen el horrible nombre de «bariones»); otras, como los piones están constituidas por un quark y un antiquark (y se denominan «mesones»).
Déjenme construir una tabla de partículas fundamentales tal como aparecen en la actualidad (ver Fig. 79). Comenzaré por las partículas que van de punto a punto según la fórmula E(A a B) —modificada por el mismo tipo de reglas de polarización del electrón—, llamadas «partículas de espín 1/2». La primera de estas partículas es el electrón y su número másico es 0,511 en unidades que usaremos todo el tiempo y que denominaremos MeV[25].

FIGURA 79. A Nuestra lista de todas las partículas del mundo se inicia con las partículas de «espín 1/2»: el electrón (con una masa de 0,511 MeV), y dos «aromas» de quark, d y u (ambos con una masa de alrededor de 10 MeV). Los electrones y quarks tienen una «carga» —es decir, se acoplan con fotones con los siguientes valores (en términos de la constante de acoplamiento −j) = −1, −1/3 y +2/3.
Debajo del electrón dejaré un espacio en blanco (que ocuparemos posteriormente), debajo del cual situaré dos tipos de quarks —el d y el u—. La masa de estos quarks no se conoce con exactitud, una buena aproximación es de alrededor de 10 MeV cada uno. (El neutrón es ligeramente superior al protón, lo que parece implicar —como verán en seguida— que el quark d es ligeramente más pesado que el quark u).
Al lado de cada partícula colocaré su carga, o constante de acoplamiento, en términos de −j, el número de acoplamiento con fotones invertido de signo. Esto hace que la carga del electrón sea −1, consistente con el convenio iniciado por Benjamin Franklin y al que desde entonces nos hemos adherido. Para el quark d la amplitud de acoplamiento con un fotón es −1/3, y para el quark u es +2/3 (si Benjamin Franklin hubiese sabido de los quarks, ¡hubiese tomado la carga del electrón, al menos, como −3!).
Entonces, la carga del protón es +1 y la carga del neutrón es cero. Jugando un poco con los números se puede ver que el protón —hecho de tres quarks— debe tener dos u, y un d mientras que el neutrón —también formado por tres quarks— debe tener dos d y un u (ver Fig. 80).

FIGURA 80. Todas las partículas formadas por quarks, de las cuales el protón y el neutrón son los ejemplos más comunes, vienen en una de las dos posibles clases: las constituidas por un quark y un anti-quark, y las constituidas por tres quarks. La carga de los quarks d y u se combina para dar +1 para el protón y cero para el neutrón. El hecho de que el protón y el neutrón estén formados por partículas cargadas moviéndose dentro de ellos da una pista de por qué el protón tiene un momento magnético superior a 1, y por qué el supuestamente neutro neutrón tiene un cierto momento magnético.
¿Qué mantiene unidos a los quarks? ¿Los fotones que se mueven entre ellos? (Puesto que un quark d tiene una carga de −1/3 y un quark u de +2/3, los quarks, además de electrones, emiten y absorben fotones). No, estas fuerzas eléctricas son demasiado débiles para hacerlo. Se ha inventado algo más, que al viajar de uno a otro quark los mantiene unidos; algo llamado «gluones»[26]. Los gluones son un ejemplo de otro tipo de partículas denominado «espín 1» (como son los fotones); viajan de un punto a otro con una amplitud determinada por la misma fórmula que la de los fotones, P(A a B). La amplitud para que los gluones sean emitidos o absorbidos por los quarks es un número misterioso, g, que es mucho mayor que j (ver Fig. 81).

FIGURA 81. Los «gluones» mantienen a los quarks unidos para formar protones y neutrones, e indirectamente son responsables del hecho de que los protones y neutrones se mantengan juntos en el núcleo de un átomo. Los gluones mantienen unidos a los quarks mediante fuerzas mucho más fuertes que las eléctricas. La constante de acoplamiento de los gluones, g, es mucho más grande que j, lo que hace mucho más difíciles los cálculos de los términos con acoplamientos: la mayor precisión que se puede esperar de momento es del 10%.
Los diagramas que construimos de quarks intercambiando gluones son muy similares a los dibujos que hicimos de los electrones intercambiando fotones (ver Fig. 82). Tan parecidos, de hecho, que pueden Vds. decir que los físicos carecen de imaginación —¡simplemente han copiado la teoría de la electrodinámica cuántica para las interacciones fuertes!—. Y tendrán razón: es lo que hicimos, pero con un ligero cambio.

FIGURA 82. El diagrama de uno de los caminos por el que dos quarks pueden intercambiar un gluón es tan similar al de dos electrones intercambiando un fotón que Vds. pueden pensar que los físicos han copiado, para la teoría de las «interacciones fuertes» que mantiene unidos a los quarks dentro de los protones y neutrones, la teoría de la electrodinámica cuántica. Bien, lo han hecho —casi.
Los quarks tienen un tipo de polarización adicional que no está relacionada con la geometría. Los idiotas de los físicos, incapaces de encontrar alguna maravillosa palabra griega, bautizaron a este tipo de polarización con el desafortunado nombre de «color», que no tiene nada que ver con el color habitual. En un momento dado, el quark puede estar en una de las tres condiciones o «colores» —R, G o B (¿pueden imaginar que significa?)[27]—. El «color» de un quark puede combinarse cuando el quark emite o absorbe un gluón. Los gluones vienen en ocho tipo diferentes, de acuerdo con los «colores» con que pueden acoplarse. Por ejemplo, si un quark rojo cambia a verde, emite un gluón rojo-antiverde[28] —un gluón que toma el rojo de quark y cede el verde— («antiverde» significa que el gluón está transportando al verde en la dirección opuesta). Este gluón puede ser absorbido por el quark verde, que cambia a rojo (ver Fig. 83). Existen ocho posibles gluones distintos, tales como rojo-antirrojo, rojo-antiazul, rojo-antiverde, etc. (pensarán que eran nueve, pero por razones técnicas, faltó uno). La teoría no es muy complicada. La regla completa de los gluones es: los gluones se acoplan con cosas con «color» —sólo se precisa un poco de contabilidad para seguir el rastro de a dónde van los «colores».

FIGURA 83. La teoría gluónica difiere de la electrodinámica en que los gluones se acoplan con cosas que tienen «color» (con una de las tres posibles condiciones —«rojo», «verde», y «azul»—). Aquí, un quark u cambia a verde emitiendo un gluón rojo-antiverde que es absorbido por un quark d verde que cambia a rojo (si el «color» se transporta hacia atrás en el tiempo, adquiere el prefijo «anti»).
Existe, sin embargo, una interesante posibilidad creada por esta regla: los gluones se pueden acoplar con otros gluones (ver Fig. 84). Por ejemplo, un gluón verde-antiazul encontrándose con un gluón rojo-antiverde resulta en un gluón rojo-antiazul. La teoría de los gluones es muy sencilla —se dibuja el diagrama y se siguen los «colores». La magnitud de los acoplamientos en todos los diagramas viene determinada por la constante de acoplamiento para gluones, g.

FIGURA 84. Puesto que los gluones tienen también «color» se pueden acoplar entre sí. Aquí un gluón verde-antiazul se acopla con un gluón rojo-antiverde para formar un gluón rojo-antiazul. La teoría gluónica es fácil de entender —sólo hay que seguir los «colores».
La teoría de los gluones no es muy distinta formalmente de la electrodinámica cuántica. Entonces, ¿cómo se compara con los experimentos? Por ejemplo, ¿cómo es el momento magnético observado del protón cuando se compara con el valor calculado de la teoría?
Los experimentos son muy precisos —demuestran que el valor del momento magnético es 2,79275—. En el mejor de los casos, la teoría sólo puede dar 2,7 ± 0,3 —si uno es lo suficientemente optimista sobre la precisión de su análisis ¡un error de 10% que es 10 000 veces más impreciso que el experimento! Tenemos una teoría sencilla, definida, que se supone que explica todas las propiedades de los protones y neutrones, y sin embargo no se puede calcular nada con ella porque las matemáticas son demasiado complicadas para nosotros. (Pueden imaginarse lo que estoy tratando de hacer, y no me lleva a ninguna parte). La razón por la que no podemos calcular nada con mayor precisión se debe a la constante de acoplamiento de los gluones g, que es mucho más grande que la de los electrones. Términos con dos, cuatro, e incluso seis acoplamientos, no son meras correcciones menores a la amplitud principal; representan contribuciones considerables que no se pueden ignorar. De manera que hay flechas de tantas posibilidades diferentes que no hemos sido capaces de organizarlas de manera razonable para encontrar cuál es la flecha final.
En los libros se dice que la ciencia es sencilla: se hace una teoría y se compara con los experimentos; si la teoría no funciona, se descarta y se hace una nueva teoría. Aquí tenemos una teoría definida y cientos de experimentos pero ¡no podemos compararlos! Es una situación que nunca antes había existido en la historia de la física. Nos encontramos temporalmente encajonados, incapaces de dar con un método de cálculo. Estamos enterrados bajo una capa de flechitas.
A pesar de nuestras dificultades para realizar cálculos con la teoría, entendemos algunas cosas, cualitativamente, gracias a la cromodinámica cuántica (las interacciones fuertes de quarks y gluones). Los objetos compuestos de quarks, que vemos, son de «color» neutro: los grupos de tres quarks contienen un quark de cada «color» y los pares quark-antiquark tienen la misma amplitud de ser rojo-antirrojo, verde-antiverde o azul-antiazul. También entendemos el por qué los quarks nunca se pueden producir como partículas individuales —el por qué, independientemente de cuanta energía se utilice para hacer chocar un núcleo contra un protón, en lugar de observar la aparición de quarks individuales, vemos un haz de mesones y bariones (pares quark-antiquark y grupos de tres quarks).
La cromodinámica cuántica y la electrodinámica cuántica no son todo en la física. De acuerdo con ellas, un quark no puede cambiar su «aroma»: un quark u siempre será un quark u; un quark d siempre será un quark d. Pero la Naturaleza en ocasiones se comporta de manera diferente. Existe una forma de radiactividad que tiene lugar lentamente —del tipo de la que le preocupa a la gente que se pueda escapar de los reactores nucleares— denominada desintegración beta, que implica un neutrón cambiando a protón. Puesto que un neutrón está formado por dos quarks d y un quark u, mientras que un protón se hace con dos u y un d, lo que realmente ocurre es que uno de los quarks tipo d del neutrón se cambia a un quark tipo u (ver Fig. 85). Y así es como ocurre: el quark d emite algo nuevo análogo a un fotón, denominado un W, que se acopla con un electrón y con otra partícula nueva llamada anti-neutrino, un neutrino que va hacia atrás en el tiempo. El neutrino es otra partícula de espín 1/2 (como el neutrón y los quarks) pero sin masa ni carga (no interacciona con los fotones). Tampoco interacciona con los gluones, sólo se acopla con los W (ver fig 86).

FIGURA 85. Cuando un neutrón se desintegra en un protón (un proceso denominado «desintegración beta») lo único que cambia es el «aroma» de un quark —de d a u emitiéndose un electrón y un anti-neutrino. Este proceso es relativamente lento, por lo que se ha propuesto la existencia de una partícula intermedia (denominada un «bosón intermedio W») con una masa muy elevada (de alrededor de 80 000 MeV) y una carga de +1.
La W es una partícula tipo 1 (como el fotón y el gluón) que cambia el «aroma» de un quark y se lleva su carga —el d, carga −1/3, cambia a u, carga +2/3 ¡una diferencia de −1! (No cambia el «color» del quark)—. Dado que el W− toma una carga de −1 (y su antipartícula, el W+ toma una carga de +1), también se puede acoplar con un fotón. La desintegración beta dura mucho más que las interacciones de fotones y electrones, de modo que se piensa que el W debe de tener una masa muy elevada (alrededor de 80 000 MeV), a diferencia del fotón y del gluón. No hemos sido capaces de observar el W aislado, debido a la energía tan elevada que requiere el arrancar una partícula con una masa tan grande[29].

FIGURA 86. El W se acopla con el electrón y el neutrino por un lado y el quark d y el u por el otro.
Existe otra partícula, que podríamos considerarla como una W neutra, denominada Z0. La Z0 no cambia la carga del quark, pero se acopla con un quark d, un quark u, un electrón, un neutrino (ver Fig. 87). Esta interacción tiene el equívoco nombre de «corriente neutra» y produjo mucha excitación cuando se descubrió hace unos pocos años.
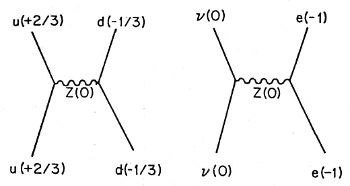
FIGURA 87. Cuando no hay cambio de carga en ninguna de las partículas, el W tampoco tiene carga (se denomina en este caso Z0). Estas interacciones se denominan «corrientes neutras». Aquí se muestran dos posibilidades.
La teoría de las W es clara y bonita si se permiten tres tipos de acoplamiento entre tres tipo de W (ver Fig. 88). La constante de acoplamiento observada para el W es muy similar a la del fotón —en el entorno de j.

FIGURA 88. Es posible un acoplamiento entre un W−1 y su antipartícula (un W+1) y un neutro W (Z0). La constante de acoplamiento para W es próxima a j, sugiriendo que los W y los fotones pueden ser distintos aspectos de la misma cosa.
Por tanto, existe la posibilidad de que los tres W y el fotón sean aspectos diversos de la misma cosa. Stephen Weinberg y Abdus Salam intentaron combinar la electrodinámica cuántica con lo que se denomina «interacción débil» (interacción con los W) en una única teoría cuántica y lo consiguieron. Pero si Vds. miran los resultados que obtuvieron se puede ver el pegamento[30] por así decirlo. Está claro que el fotón y los tres W están de alguna manera interconectados, pero al nivel actual de conocimiento es difícil ver la conexión con claridad —todavía se pueden ver las «costuras» en las teorías; aún no se han pulido de forma que las conexiones sean más hermosas y por tanto, probablemente más correctas.
Así que aquí estamos: la teoría cuántica tiene tres tipos principales de interacción —las «interacciones fuertes» de quarks y gluones, las «interacciones débiles» de los W y las «interacciones eléctricas» de los fotones—. Las únicas partículas del mundo (de acuerdo con este esquema) son los quarks (en «aroma» u y d, con tres «colores» cada uno), los gluones (ocho combinaciones de R, G y B), los W (cargados ±1 y 0), los neutrinos, electrones y fotones —alrededor de veinte partículas diferentes de seis tipos distintos (más sus antipartículas)—. No está mal —alrededor de veinte partículas diferentes— excepto que esto no es todo.
Al hacer incidir sobre los núcleos protones de energía cada vez más alta, siguieron apareciendo nuevas partículas. Una de ellas fue el muón, que es en todos los aspectos idéntico al electrón, salvo que su masa es mucho más elevada —105,8 MeV comparada con 0,511 para el electrón, o alrededor de 206 veces más pesado—. ¡Es como si Dios quisiera probar un número distinto para la masa! Todas las propiedades del muón se pueden describir completamente por la teoría de la electrodinámica —la constante de acoplamiento j es la misma y E(A a B) también; sólo se necesita poner un valor distinto de n[31].
Dado que el muón tiene una masa aproximadamente 200 veces más grande que la del electrón, la «manecilla del cronógrafo» para un muón gira 200 veces más deprisa que para un electrón. Esto nos ha permitido verificar si la electrodinámica todavía se comporta como establece la teoría a distancias 200 veces más pequeñas de lo que habíamos sido capaces antes de probar —aunque estas distancias son todavía más de ocho cifras decimales superiores a las distancias a las que la teoría puede tener problemas debido a los infinitos.

FIGURA 89. En el proceso de bombardear núcleos con protones de energías más y más altas, aparecen nuevas partículas. Una de ellas es el muón, o electrón pesado. La teoría que describe las interacciones del muón es exactamente la misma que para el electrón, excepto que se introduce un número más elevado para n en E(A a B). El momento magnético de un muón debería ser ligeramente diferente del electrón a dos alternativas especiales: cuando el electrón emite un fotón que se desintegra en un par electrón-positrón o muón-antimuón, la desintegración crea un par que tiene una masa próxima o muy superior a la del electrón. Por otro lado, cuando el muón emite un fotón que se desintegra en un par muón-antimuón o positrón-electrón, este par tiene una masa próxima o mucho más ligera que la masa del muón. Los experimentos confirman esta ligera diferencia.
Veamos si el muón puede estar implicado en un proceso radiactivo como la desintegración beta: cuando un quark d cambia a un quark u emitiendo un W, ¿puede el W acoplarse con un muón en lugar de con un electrón? Sí (ver Fig. 90). ¿Y qué ocurre con el anti-neutrino? En el caso de acoplamiento del W con un muón, una partícula denominada neutrino-mu ocupa el lugar del neutrino ordinario (que denominaremos ahora un neutrino electrónico). De modo que nuestra tabla de partículas tiene dos partículas adicionales próximas al electrón y al neutrino —el muón y el neutrino-mu.

FIGURA 90. El W tiene una cierta amplitud de emisión de un muón en lugar de un electrón. En este caso un neutrino-mu reemplaza a un neutrino electrónico.
¿Y que ocurre con los quarks? Enseguida se supo que las partículas tenían que estar formadas por quarks más pesados que el u o el d. Así, se incluyó un tercer quark, denominado s (por «extraño»[32] (+))en la lista de partículas elementales. El quark s tiene una masa de unos 200 MeV, comparada con unos 20 MeV para los quarks u y d.
Durante muchos años pensamos que había tres «aromas» de quarks —u, d y s— pero, en 1974, se descubrió una nueva partícula denominada mesón-pi que no podía estar constituida por tres quarks. Existía también una buena razón teórica de que debía de haber un cuarto quark, acoplado al quark s mediante un W de la misma manera en que se acoplan un quark u y otro d (ver Fig. 91). El «aroma» de este quark se denominó c y yo no tengo agallas para explicarles de dónde proviene la c, pero puede que lo hayan leído en los periódicos[33]. ¡Los nombres van empeorando cada vez más!

FIGURA 91. La Naturaleza parece estar repitiendo las partículas de espín 1/2. Además del muón y del neutrino-mu, existen dos nuevos —s y c— que tienen la misma carga pero mayores masas que sus contrapartidas en la siguiente columna.
Esta repetición de partículas con las mismas propiedades pero masas más pesadas, es un completo misterio. ¿Qué es esta extraña duplicidad del esquema? Como el profesor I. I. Rabi dijo cuando se descubrió el muón «¿Quién lo ha ordenado?».
Recientemente ha comenzado otra repetición de la lista. Al ir a energías cada vez más altas, la Naturaleza parece continuar apilando estas partículas como para drogarnos. Tengo que hablarles de ellas porque quiero que vean lo aparentemente complejo que el mundo parece en realidad. Sería muy engañoso si les diese la impresión de que puesto que hemos resuelto el 99% de los fenómenos del mundo mediante electrones y fotones, ¡el otro 1% de los fenómenos requiriese sólo el 1% de partículas adicionales! Resulta que para explicar este 1% final, necesitamos un número diez o veinte veces mayor de partículas adicionales.
De modo que empezamos de nuevo: utilizando energías aún más elevadas en los experimentos, se ha encontrado un electrón todavía más pesado, denominado «tau»; tiene una masa de alrededor de 1800 MeV; ¡tan pesado como dos protones! También se ha inferido un neutrino-tau. Y ahora se ha encontrado una curiosa partícula que implica un nuevo «aroma» para los quarks —esta vez es «b» de «belleza» y tiene una carga de −1/3 (ver Fig. 92)—. Bien, ahora, por un momento, les quiero físicos teóricos fundamentales de primera clase y que predigan algo: se encontrará un nuevo aroma para los quarks, denominado… (de «…», con una carga de …, una masa de … MeV) —¡y ciertamente esperamos que sea verdad que exista![34]
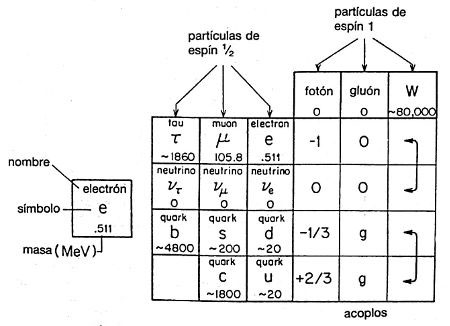
FIGURA 92. ¡Aquí estamos de nuevo! Otra repetición de las partículas de espín 1/2 se ha iniciado a energías aún más elevadas. Esta repetición será completa si se encuentra una partícula con las propiedades adecuadas para implicar la existencia de un nuevo aroma para el quark. Mientras tanto, se están realizando los preparativos para buscar los principios de otra repetición a energías todavía más elevadas. La causa de estas repeticiones es un completo misterio.
Mientras tanto, se están realizando experimentos para ver si el círculo se repite una vez más. En la actualidad se están construyendo máquinas para buscar un electrón aún más pesado que el tau. Si la masa de esta supuesta partícula es 100 000 MeV, no van a ser capaces de producirla. Si está alrededor de 40 000 MeV podrán hacerlo.
Misterios como estos ciclos que se repiten hacen que sea muy interesante ser físico teórico: ¡La Naturaleza nos proporciona unos rompecabezas tan maravillosos! ¿Por qué repite la Naturaleza el electrón, con masas 206 y 3640 veces más grandes?
Me gustaría hacer un último comentario para poder completar totalmente lo referente a las partículas. Cuando un quark d acoplándose con un W cambia a un quark u, tiene a su vez una pequeña amplitud de cambiar, en su lugar, a un quark c. Cuando un quark u se transforma en otro d, también tiene una pequeña amplitud de convertirse en un quark s y otra amplitud aún menor de cambiar a un quark b (ver Fig. 93). De modo que el W «tensa» un poco las cosas y permite a los quarks estas proporciones relativas en su amplitud para poder cambiar a otro tipo de quark, es algo completamente desconocido.
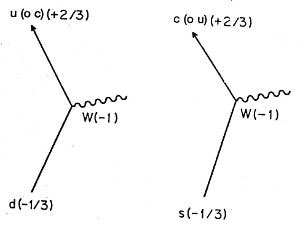
FIGURA 93. Un quark d tiene una pequeña amplitud de cambiar a un quark c en lugar de a un quark u, y un quark s tiene una pequeña amplitud de cambiar a un quark u en lugar de a un quark c, con la emisión en ambos casos de un W. De modo que el W parece ser capaz de cambiar el aroma de un quark de una a otra columna de la tabla (ver Fig. 92).
Así que, aquí está todo sobre el resto de la física cuántica. Es un lío terrible, y podrían decir que la física se ha convertido en un barullo descorazonador. Pero siempre ha tenido esta apariencia. La Naturaleza ha parecido un barullo horrible, pero al avanzar vemos esquemas y aunamos teorías; se aclaran un poco las cosas y se vuelven más sencillas. El lío que les he expuesto es mucho menor que el que hubiese tenido que contar hace diez años, hablándoles de más de un centenar de partículas. Y piensen en el lío de principios de siglo, cuando estaban el calor, magnetismo, la electricidad, la luz, los rayos-X, los rayos ultravioletas, los índices de refracción, los coeficientes de reflexión y otras propiedades de diversas substancias, cosas todas que se han unificado desde entonces en una teoría, la electrodinámica cuántica.
Me gustaría resaltar algo. Las teorías del resto de la física son muy similares a la teoría de la electrodinámica cuántica: todas implican la interacción de objetos de espín 1/2 (como electrones y quarks) con objetos de espín 1 (como fotones, gluones o W) dentro de un marco de amplitudes en donde la probabilidad de un suceso es el cuadrado de la longitud de una flecha. ¿Por qué todas las teorías físicas son tan similares en estructura?
Existen un cierto número de posibilidades. La primera, la limitada imaginación de los físicos: cuando observamos un nuevo fenómeno tratamos de encajarlo en el marco que ya tenemos —hasta que no hemos realizado un número suficiente de experimentos, no sabemos que eso no funciona—. De modo que cuando algún físico loco da una conferencia en UCLA en 1983 y dice «Esta es la manera en que ocurren las cosas y miren cuán maravillosamente similares son las teorías», no es porque la Naturaleza sea realmente similar, es porque los físicos sólo han sido capaces de pensar la condenada misma cosa una y otra vez.
Otra posibilidad es que sea la condenada misma cosa una y otra vez —que la Naturaleza sólo tenga una forma de realizar las cosas y que repita su historia de vez en cuando.
Una tercera posibilidad es que las cosas parecen similares porque son aspectos de una misma cosa —una amplia imagen subyacente de la que se pueden desgajar partes que parecen diferentes, análogo a los dedos de una mano—. Muchos físicos están trabajando muy duro tratando de componer una gran imagen que unifique todo en un supermodelo. Es un juego delicioso, pero en la actualidad ninguno de los especuladores coincide con cualquier otro especulador en cuanto a cuál es la gran imagen. Exagero sólo ligeramente cuando digo que la mayoría de estas teorías especulativas no tienen mayor sentido que la suposición que hicieron Vds. sobre la posibilidad de un quark t, ¡y les garantizó que no son mejores que Vds. a la hora de suponer la masa del quark t!
Por ejemplo, parece que el electrón, el neutrino, el quark d, y el quark u van todos juntos —de hecho, los dos primeros se acoplan con el W, como hacen los dos últimos—. En la actualidad se piensa que un quark sólo puede cambiar «colores» o «aromas». Pero quizás un quark podría desintegrarse en un neutrino acoplándose con una partícula desconocida. Bonita idea. ¿Qué ocurriría? Significaría que los protones son inestables.
Alguien construye una teoría: los protones son inestables. ¡Hacen un cálculo y encuentran que ya no existirían protones en el Universo! De manera que juegan con los números, ponen una masa más elevada a la nueva partícula y después de mucho esfuerzo predicen que el protón decaerá a una velocidad ligeramente menor que la medida la última vez cuando se demostró que el protón no decaía.
Cuando aparece un nuevo experimento y mide con más cuidado el protón, las teorías se ajustan para escaparse de la presión. El experimento más reciente mostró que el protón no decae a una velocidad cinco veces menor que la que se predijo en la última oleada de teorías. ¿Qué piensan que ocurrió? El fénix surgió de nuevo con una nueva modificación de la teoría que requiere experimentos aún más precisos para comprobarla. Si el protón decae o no es algo desconocido. Demostrar que no decae es muy difícil.
A lo largo de estas conferencias no he discutido la gravitación. La razón es que la influencia gravitacional entre objetos es extremadamente pequeña: es una fuerza que es un 1 seguido de 40 ceros más débil que la fuerza eléctrica entre dos electrones (quizá son 41 ceros). En la materia, casi todas las fuerzas eléctricas se emplean en mantener a los electrones próximos a los núcleos de sus átomos, creando un fino equilibrio mezcla de mases y menos que se cancelan entre sí. Pero con la gravitación, la única fuerza es la atracción y crece y crece según hay más y más átomos hasta que, al final, cuando obtenemos esas grandes masas ponderables que somos, empezamos a poder medir los efectos de la gravedad —sobre los planetas, sobre nosotros mismos y así sucesivamente.
Dado que la fuerza gravitacional es mucho más débil que cualquiera otra de las interacciones, es imposible, en la actualidad, hacer cualquier experimento que sea lo suficientemente delicado como para medir cualquier efecto que requiera la precisión de una teoría cuántica de la gravitación para explicarlo[35]. Pero aunque no haya manera de probarlas, existen, sin embargo, teorías cuánticas de la gravedad que implican «gravitones» (que podrían aparecer bajo una nueva categoría de polarizaciones, denominada «espín 2») y otras partículas fundamentales (algunas con espín 3/2). La mejor de estas teorías no es capaz de incluir las partículas que encontramos, inventando, no obstante, muchas partículas que no se encuentran. Las teorías cuánticas de la gravitación también tienen infinitos en los términos de acoplamiento, pero el «proceso de profundización», que tanto éxito tiene eliminando los infinitos en la electrodinámica cuántica, no puede eliminarlos en la gravitación. De modo que no sólo no tenemos experimentos con los que probar la teoría cuántica de la gravitación, sino que tampoco tenemos una teoría razonable.
A lo largo de la totalidad de esta historia ha permanecido una característica particularmente insatisfactoria: las masas observadas de las partículas, m. No existe teoría que explique adecuadamente estos números. Utilizamos los números en todas nuestras teorías, pero no los entendemos —ni lo que son, ni de dónde vienen—. Creo que desde un punto de vista fundamentalista, es un problema serio y muy interesante.
Lamento si toda esta especulación sobre las nuevas partículas les ha confundido, pero decidí completar mi discusión del resto de la física para demostrarles cómo el carácter de estas leyes —el marco de amplitudes, los diagramas que representan las interacciones que hay que calcular, y demás— parece ser el mismo que en la teoría de la electrodinámica cuántica, nuestro mejor ejemplo de una buena teoría.
Nota añadida al leer las pruebas, noviembre 1984
Desde que se dieron estas conferencias, sospechosos sucesos observados en los experimentos, parecen apuntar que, acaso, sea posible que se descubra pronto otra nueva e inesperada partícula o fenómeno (y en consecuencia no mencionado en estas conferencias).
Nota añadida al leer las pruebas, abril 1985
En este momento, los «sospechosos sucesos» mencionados anteriormente parecen ser una falsa alarma. La situación sin duda habrá cambiado de nuevo en la época en que uds. lean este libro. Las cosas cambian con mayor rapidez en la física que en el negocio de publicación de libros.