III
GLI ELETTRONI E LE LORO INTERAZIONI

Questa è la terza di quattro lezioni su un argomento abbastanza difficile, la teoria dell'elettrodinamica quantistica. Essendo presente più gente delle volte precedenti è chiaro che alcuni non hanno sentito le altre lezioni, per cui troveranno questa quasi incomprensibile. Anche chi le ha sentite la troverà incomprensibile, ma sa già che la cosa è perfettamente normale; come ho spiegato nella prima lezione il modo di cui disponiamo per descrivere la Natura ci risulta, in generale, incomprensibile.

Lo scopo di queste lezioni è di parlarvi della parte meglio conosciuta della fisica, l'interazione della luce con gli elettroni, interazione che riguarda la maggior parte dei fenomeni usuali, per esempio tutti i fenomeni chimici e tutti quelli biologici. Gli unici a restare fuori da questa teoria sono i fenomeni nucleari e quelli gravitazionali.

Come ho detto nella prima lezione, noi non disponiamo di una spiegazione che descriva in modo soddisfacente anche solo il più semplice dei fenomeni, quale la riflessione parziale della luce sul vetro. Ci è inoltre impossibile prevedere se un dato fotone sarà riflesso o attraverserà il vetro. Sappiamo solo calcolare la probabilità che accada un particolare fenomeno, ad esempio che il fotone venga riflesso. (Tale probabilità risulta circa del 4% se la luce incide perpendicolarmente su un blocco di vetro, e aumenta per un'incidenza più obliqua).

In situazioni abituali si hanno le seguenti «regole di composizione» per le probabilità: 1) se qualcosa può verificarsi in modi alternativi, le varie probabilità vanno sommate; 2) se un fenomeno si presenta come successione di passi, o dipende dall’avverarsi concomitante di più eventi indipendenti, si devono moltiplicare tra loro le probabilità per ciascun passo o per ciascun evento.

Nel mondo misterioso e affascinante della fisica quantistica le probabilità vengono invece calcolate come quadrati della lunghezza di una freccia: là dove in circostanze ordinarie ci si aspetterebbe di dover sommare probabilità, ci si trova a dover ‘sommare’ frecce; dove ci si aspetterebbe di moltiplicare probabilità, si devono ‘moltiplicare’ frecce. Le risposte che si ottengono calcolando le probabilità in questo modo, per quanto strane, riproducono esattamente i risultati sperimentali. Personalmente trovo bellissimo dover ricorrere a queste strane regole e a questo strano modo di ragionare per descrivere la Natura, e mi piace parlarne agli altri. È un'analisi che non nasconde nessun congegno segreto: se si vuole capire la Natura, la strada è questa.

Prima di entrare nel vivo della lezione, vi darò un altro esempio del comportamento della luce. Prendiamo una luce monocromatica molto flebile (un fotone alla volta) che viaggia dalla sorgente in S al rivelatore in D (fig. 49).

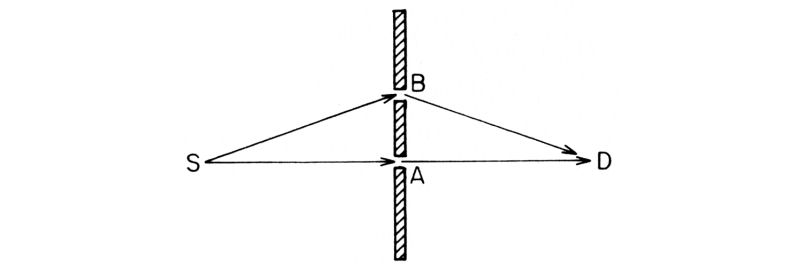
Fig. 49. In uno schermo interposto tra la sorgente S e il rivelatore D vi sono, in A e in B, due fori piccolissimi. Quando sono aperti alternativamente, attraverso ciascuno di essi giunge al rivelatore quasi la stessa quantità di luce (in questo esempio l'1%). Se i fori sono entrambi aperti, c'è «interferenza»: la probabilità che il rivelatore ticchetti varia tra zero e il 4% a seconda della separazione tra A e B (fig. 51 a).

Tra sorgente e rivelatore interponiamo uno schermo in cui vi sono due piccolissimi fori, in A e in B, distanti tra loro alcuni millimetri. (Se sorgente e rivelatore distano 100 centimetri tra loro, il diametro dei fori deve essere inferiore a un decimo di millimetro). Sia A allineato con S e con D, mentre B, trovandosi lateralmente, non è sulla stessa linea.

Quando il foro in B è chiuso, il rivelatore in D ticchetta con una certa frequenza, corrispondente al numero di fotoni che arrivano attraverso A: mettiamo che faccia in media un «clic» ogni 100 fotoni partiti da S. Come abbiamo visto nella seconda lezione, se si chiude il foro in A e si apre quello in B, il contatore ticchetta in media quasi con la stessa frequenza, dato che i fori sono molto piccoli. (Se si 'comprime' troppo la luce non risultano più valide le regole del mondo usuale, ad esempio che la luce viaggia in linea retta). Quando entrambi i fori sono aperti, otteniamo una risposta complicata perché si verifica interferenza: per certe distanze tra i due fori il numero di scatti del rivelatore è maggiore del 2% che ci si aspetta (con un massimo di circa il 4%); per distanze anche pochissimo diverse non si verifica alcuno scatto.

Verrebbe spontaneo pensare che l'apertura di un secondo foro debba sempre aumentare la quantità di luce che arriva nel rivelatore, ma nella realtà non accade così. Pertanto è sbagliato dire che la luce viaggia «seguendo questo percorso oppure quest'altro». Io stesso mi sorprendo talvolta a dire: «O andrà di qua o andrà di là», ma nel dire così devo tenere a mente che in realtà sto parlando di ampiezze da sommare: il fotone ha un'ampiezza relativa a un percorso e un'ampiezza relativa all'altro percorso. Se le due ampiezze sono opposte non arriva luce nel punto considerato, anche quando, come nel nostro caso, entrambi i fori sono aperti.

Ed ecco un'ulteriore complicazione nello strano comportamento della Natura. Supponiamo di mettere, in A e in B, opportuni rivelatori che indichino attraverso quale dei due fori passa il fotone quando sono entrambi aperti (è possibile costruire un rivelatore che segnali il passaggio di un fotone senza assorbirlo) (fig. 50). Poiché la probabilità che un fotone vada da S a D dipende dalla distanza tra i fori, il fotone deve per forza dividersi in due furtivamente e poi ricomporsi di nuovo. Giusto? Secondo questa ipotesi, i rivelatori in A e in B dovrebbero sempre scattare insieme (magari con intensità dimezzata), mentre il rivelatore in D dovrebbe scattare con probabilità da zero al 4%, a seconda della distanza tra i fori A e B.

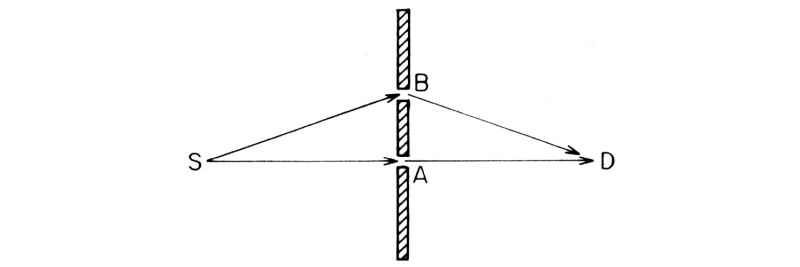
Fig. 50. Se in A e in B si inseriscono speciali rivelatori per determinare attraverso quale dei due fori passa la luce quando sono entrambi aperti, si è cambiato esperimento. Poiché quando i fori sono tenuti sotto controllo il fotone passa sempre o attraverso l'uno o attraverso l'altro, esistono ora due condizioni finali distinguibili: 1) scattano i rivelatori in A e in D, 2) scattano i rivelatori in B e in D. Ciascuno di questi due eventi si verifica con probabilità di circa l'1%. Le probabilità vanno sommate tra loro nel modo normale e si ha una probabilità complessiva del 2% che scatti il rivelatore in D (fig. 51 b).

Invece, nella realtà, i rivelatori in A e in B non scattano mai assieme: o scatta A o scatta B. Il fotone non si divide in due: o segue un percorso o segue l'altro.

Inoltre in presenza dei rivelatori A e B il rivelatore in D scatta esattamente il 2% delle volte, la semplice somma delle probabilità per i percorsi A e B: 1% + 1%. Tale valore non è influenzato dalla distanza tra A e B; l'interferenza scompare se si pongono dei rivelatori in A e in B!

La Natura ha congegnalo le cose così bene che non riusciremo mai a capire dove sta il trucco: inserendo gli strumenti opportuni possiamo stabilire qual è il percorso seguito dalla luce, ma i bellissimi effetti di interferenza scompaiono. Se non ci sono strumenti rivelatori, gli effetti di interferenza ritornano! Decisamente molto strano!

Per risolvere questo paradosso, vi ricorderò un principio fondamentale: per calcolare correttamente la probabilità di un evento si deve definire con chiarezza l'evento completo, in particolare quali siano le condizioni iniziali e finali dell'apparato. Si devono controllare gli strumenti di misura prima e dopo l'esperimento e cercare le eventuali variazioni. Quando prima calcolavamo la probabilità che un fotone vada da S a D senza rivelatori in A e in B, il fenomeno consisteva semplicemente nello scatto del rivelatore in D. Quando tale scatto era l'unico cambiamento nell'apparato di misura, non c'era modo di conoscere il percorso scelto dal fotone e si osservava interferenza.

Mettendo rivelatori in A e in B, abbiamo cambiato il problema. Adesso ci sono due eventi completi, cioè due insiemi di condizioni finali, distinguibili: 1) scattano i rivelatori in A e in D, 2) scattano i rivelatori in B e in D. Essendovi diverse condizioni finali possibili, si deve calcolare la probabilità di ciascuna di esse come evento separato e completo.

Per calcolare la probabilità che vi sia uno scatto nei rivelatori in A e in D, si devono moltiplicare le frecce che rappresentano i seguenti passi: un fotone va da S ad A, poi da A a D e il rivelatore in D scattali quadrato della freccia finale dà la probabilità di questo evento. Essa risulta l'1%, cioè la stessa di quando il foro in B è chiuso, perché in ambedue i casi si hanno gli stessi passi. L'altro evento completo è lo scatto dei rivelatori in B e in D. La relativa probabilità si calcola in modo analogo e anch'essa è circa 14%, la stessa di quando A è chiuso.

Se si vuole sapere con che frequenza ticchetta il contatore in D e non interessa se nel contempo è scattato A o è scattato B, la probabilità è la semplice somma delle probabilità dei due eventi: il 2%. Anche nei casi in cui si trascura qualcosa che avrebbe potuto essere osservato per discriminare il percorso seguito dal fotone, siamo di fronte a «stati finali» differenti, cioè a condizioni finali distinguibili, e si devono sommare le probabilità relative a ciascuno di essi, non le ampiezze.¹⁴

Ho voluto mettere in evidenza queste cose perché quanto più si vede la stranezza del comportamento della Natura, tanto più si capisce perché sia difficile costruire un modello intuitivo che riesca a descrivere anche i fenomeni più semplici. Perciò la fisica teorica ha rinunciato a farlo.

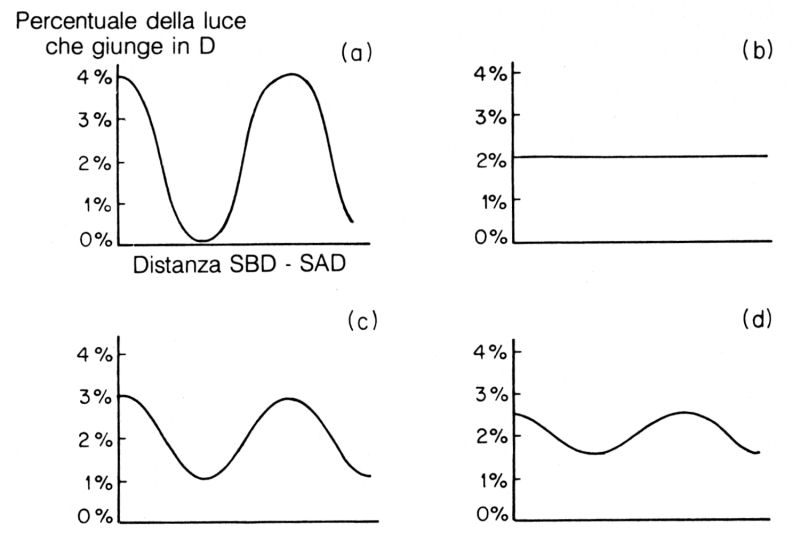
Fig. 51. Se in A e in B non vi sono rivelatori, si produce interferenza: la quantità di luce in D varia tra zero e il 4% (a). Se in A e in B vi sono rivelatori con efficienza del 100%, non si produce interferenza: la quantità di luce che giunge in D è sempre il 2% (b). Se i rivelatori in A e in B non sono completamente affidabili (cioè se qualche volta non viene compiuta nessuna misura in A o in B), vi sono tre condizioni finali distinguibili: scattano A e D, scattano B e D, scatta solamente D. La curva che si ottiene in questo caso è la semplice sovrapposizione dei contributi di ciascuna condizione finale possibile. Meno affidabili sono i rivelatori in A e in B, maggiore è l'interferenza. Ad esempio, i rivelatori nel caso (c) sono meno affidabili che nel caso (d). La quantità di interferenza è determinata dal seguente principio: si deve calcolare indipendentemente la probabilità per ciascuna delle condizioni finali differenti, sommando le relative frecce e prendendo il quadrato della freccia finale; queste probabilità vanno poi sommate tra loro nel modo usuale.

Nella prima lezione ho mostrato come un evento possa essere diviso in più modi alternativi e come vadano ‘sommate’ le frecce relative a ciascuno di essi. Nella seconda lezione si è poi visto come ogni modo può essere suddiviso in passi successivi, come le frecce per ciascun passo possono considerarsi trasformazioni di una freccia unitaria e come esse vadano ‘moltiplicate’ tra loro con contrazioni e rotazioni successive. Conosciamo così tutte le regole necessarie per tracciare e combinare tra loro le frecce (che rappresentano i vari pezzi di un fenomeno) in modo da ottenere la freccia finale il cui quadrato dà la probabilità che esso si verifichi.

È naturale chiedersi fino a che punto si possa spingere tale procedimento di suddivisione degli eventi in sottoeventi via via più semplici. Quali sono le parti più elementari che costituiscono un evento? Esiste un numero limitato di pezzi con cui è possibile ottenere tutti i fenomeni che coinvolgono la luce e gli elettroni? C'è un numero limitato di ‘lettere’ nel linguaggio dell'elettrodinamica quantistica le cui combinazioni formano le ‘parole’ e le ‘frasi‘ che costituiscono la quasi totalità dei fenomeni naturali?

La risposta è sì, e il numero è tre. Ci sono solo tre eventi elementari di base, necessari per dar luogo a tutti i fenomeni associati con la luce e gli elettroni. Prima di introdurre tali eventi devo presentarvi gli attori, cioè i fotoni e gli elettroni. Dei fotoni, particelle di luce, si è parlato a lungo nelle prime due lezioni. Gli elettroni furono scoperti nel 1895 e classificati come particelle, essendo possibile contarli o aggiungerne uno a una goccia d'olio e misurarne la carica. A poco a poco si comprese che è il movimento di queste particelle a costituire la corrente elettrica che passa nei fili conduttori.

Nei primi tempi successivi alla scoperta degli elettroni si pensò che gli atomi fossero come piccoli sistemi solari, formati da una parte centrale pesante, detta nucleo, e dagli elettroni che le girano attorno seguendo delle 'orbite', come pianeti attorno al sole. Chi pensa che gli atomi siano fatti così è fermo al 1910. Nel 1924 Louis de Broglie suggerì che agli elettroni vada associato un aspetto ondulatorio, e poco tempo dopo C.J. Davisson e L.H. Germer, dei Laboratori Bell, bombardando con elettroni un cristallo di nickel, trovarono che essi rimbalzano con angoli assai curiosi (proprio come fanno i raggi X), e che questi angoli coincidono con quelli previsti dalla formula di de Broglie per la lunghezza d'onda degli elettroni.

I fenomeni osservati quando i fotoni viaggiano su distanze grandi, molto maggiori di quella necessaria per un giro completo della lancetta del cronometro, sono descritti con ottima approssimazione da leggi quali «la luce viaggia in linea retta», perché attorno al percorso di tempo minimo ci sono abbastanza percorsi che si rinforzano tra loro, e insieme c'è un numero sufficiente di altri percorsi che si cancellano tra loro. Ma quando lo spazio a disposizione di un fotone diventa troppo esiguo (come nel caso dei piccoli fori nello schermo), queste leggi non sono più valide: si osserva allora che la luce non viaggia necessariamente in linea retta, che vi è interferenza causata dai due fori e così via. La medesima situazione si presenta con gli elettroni: su grandi distanze si propagano come particelle, lungo percorsi definiti. Ma per piccole distanze, come all'interno di un atomo, lo spazio è così esiguo che non vi è un percorso dominante, non vi è ‘orbita’; l'elettrone segue tutti i possibili percorsi, ciascuno con la relativa ampiezza. L'effetto di interferenza diventa molto importante e occorre sommare le frecce per prevedere la probabilità che l'elettrone si trovi in un dato punto.

È interessante osservare che gli elettroni vennero dapprima considerati come particelle, e che il loro aspetto ondulatorio fu scoperto solo in un secondo tempo. La luce invece, a parte il caso di Newton che per errore le attribuiva natura ‘corpuscolare’, venne ritenuta dapprima un fenomeno ondulatorio e solo più tardi si scoprirono le sue caratteristiche corpuscolari. In realtà tanto gli elettroni quanto la luce si comportano un po' come onde e un po' come particelle. Piuttosto che introdurre nuovi vocaboli, tipo «partonde», si è scelto di continuare a chiamarle «particelle», tenendo però sempre presente che si comportano secondo le regole di somma e combinazione delle frecce spiegate in queste lezioni. A quanto pare, tutte le «particelle» esistenti in Natura — quark, gluoni, neutrini e altre specie di cui parlerò nella prossima lezione — presentano tale comportamento quanto-meccanico.

Ecco dunque i tre eventi elementari di base costituenti tutti i fenomeni in cui intervengono luce ed elettroni:

1. un fotone si propaga da un punto a un altro;
2. un elettrone si propaga da un punto a un altro;
3. un elettrone emette o assorbe un fotone.

A ognuno di questi eventi elementari corrisponde un'ampiezza (una freccia) che può essere determinata in base a precise regole. Discuterò tra un istante queste leggi che permettono di costruire il mondo intero (esclusi, come al solito, i fenomeni nucleari e gravitazionali!).

Debbo premettere che la scena su cui si svolgono i fatti non è solo lo spazio, ma è lo spazio e il tempo. Finora ho trascurato gli aspetti riguardanti il tempo, quali l'istante esatto in cui un fotone lascia la sorgente o in cui arriva al rivelatore. Sebbene lo spazio sia tridimensionale, nel disegnare i grafici¹⁵ considererò solo una dimensione: la collocazione spaziale di un oggetto verrà riportata sull'asse orizzontale e quella temporale sull'asse verticale.

Il primo evento che disegnerò nello spazio e nel tempo, o nello spazio-tempo come potrei inavvertitamente chiamarlo, è una palla ferma (fig. 52). Giovedì mattina, indicato con T₀, la palla occupa una certa posizione, indicata con X₀. Alcuni istanti dopo, a T₁, occuperà ancora la stessa posizione, perché sta ferma. Più tardi ancora, a T₂, la palla sarà sempre in X₀. Il grafico relativo alla palla ferma è quindi una striscia che sale verticalmente e che corrisponde alla zona occupata dalla palla.

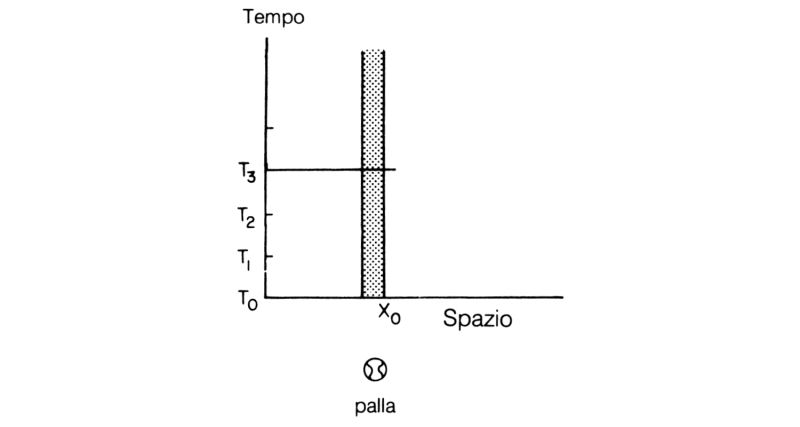
Fig. 52. Tutti gli avvenimenti dell'universo si svolgono nello spazio-tempo. Questo ha quattro dimensioni, tre spaziali e una temporale, ma verrà rappresentato in due sole dimensioni: una spaziale, lungo l'orizzontale, e una temporale, lungo la verticale. In qualunque istante si guardi una palla ferma (ad esempio a T₃), la si trova nello stesso posto. Al passare del tempo si ottiene pertanto una «striscia della palla» diretta verticalmente.

Che cosa succede se la palla si muove diritta verso un muro in assenza di gravità? Giovedì mattina, a T₀ si trova in X₀ (fig. 53), ma dopo un po' non sarà più nello stesso posto: si sarà spostata di un po' e si troverà in X₁. Via via che la palla si sposta, nel diagramma spaziotemporale si forma una corrispondente «striscia della palla», questa volta inclinata. Urtando il muro, al quale corrisponde una striscia verticale perché è fermo, la palla rimbalza all'indietro e ripassa per X₀ da dove è partita, ma a un istante di tempo differente, T₆.

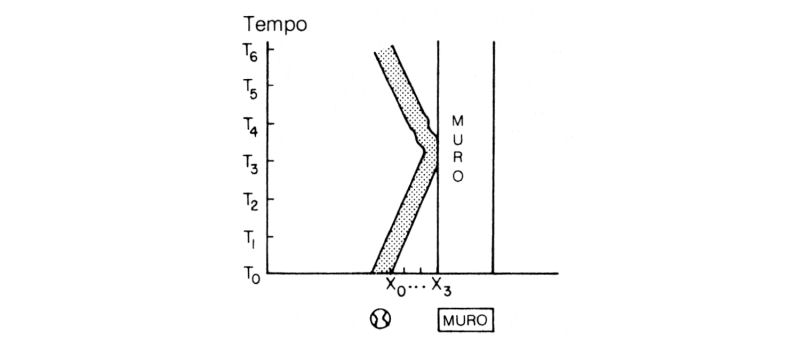
Fig. 53. Una palla in moto perpendicolarmente verso una parete sulla quale rimbalza tornando alla posizione iniziale (indicata sotto il grafico con X₀) si muove in una sola direzione e dà luogo a una «striscia della palla» inclinata. Agli istanti T₁ e T₂ la palla si avvicina alla parete, all'istante T₃ la urta e comincia a tornare indietro.

Per comodità è preferibile scegliere per la scala dei tempi un'unità di misura molto più piccola del secondo. Poiché si avrà a che fare con fotoni ed elettroni, che si muovono molto velocemente, una linea inclinata a 45° rappresenterà qualcosa che si muove alla velocità della luce. Dunque, per una particella che si sposta da X₁T₁ a X₂T₂ con tale velocità, la distanza orizzontale tra X₁ e X₂ è uguale a quella verticale tra T₁ e T₂ (fig. 54).

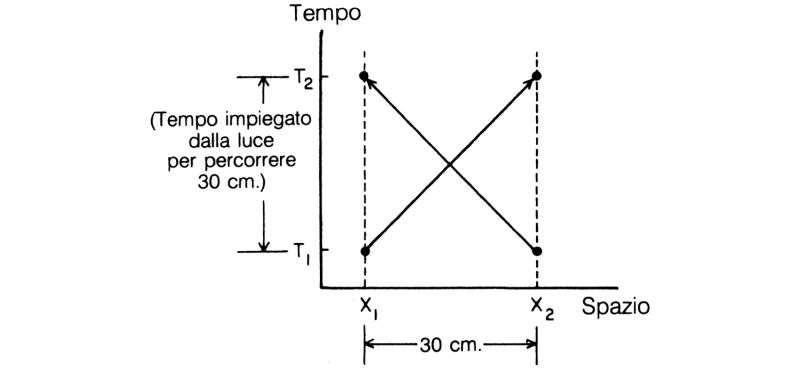
Fig. 54. La scala dei tempi usata nei grafici è tale che particelle che viaggiano alla velocità della luce sono rappresentate da linee inclinate a 45° nello spazio-tempo. Il tempo impiegato dalla luce per percorrere 30 centimetri, ad esempio da X₁ a X₂ o viceversa, è circa un miliardesimo di secondo.

Il fattore per cui moltiplicare il tempo (in modo che un angolo di 45° corrisponda alla velocità della luce) viene chiamato c. Nelle formule di Einstein si trovano dappertutto fattori c, dovuti alla infelice scelta, come unità di misura del tempo, del secondo invece che del tempo impiegato dalla luce a percorrere un metro.

Passiamo ora ad analizzare il primo evento elementare: un fotone che viaggia da un punto a un altro. Questo evento verrà rappresentato, senza particolare motivo, da un linea ondulata che va da A a B. Forse, però, dovrei essere più preciso e dire: un fotone che si trova in un dato punto a un dato istante ha una certa ampiezza per arrivare in un altro punto in un altro istante. Nel mio grafico spaziotemporale (fig. 55) un fotone inizialmente nel punto A, cioè in X₁ e T₁, ha una certa ampiezza di probabilità di comparire nel punto B, in X₂ e T₂. Indicherò questa ampiezza con F(da A a B).

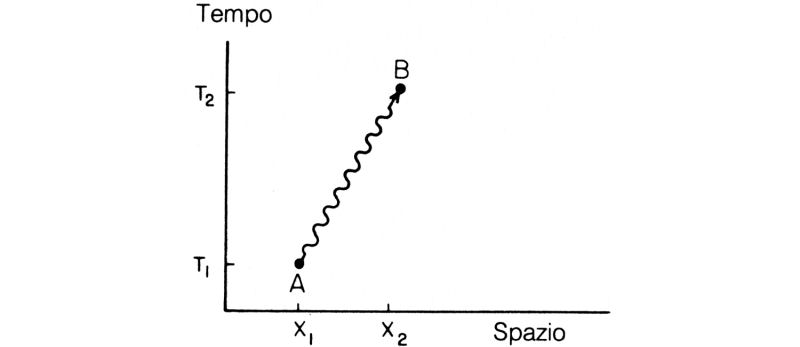
Fig. 55. Un fotone, rappresentato come una linea ondulata, ha un'ampiezza di probabilità per andare da un punto A a un punto B dello spazio-tempo che è indicata con F(da A a B) ed è espressa da una formula che dipende solo dalla differenza di posizione (X₂—X₁) e dalla differenza di tempo (T₂—T₁). In effetti è semplicemente l'inverso della differenza dei loro quadrati, cioè dell'«intervallo» I che può essere scritto (X₂ — X₁)² — (T₂—T₁)².

C'è una formula precisa per la quantità F(da A a B). È una delle grandi leggi della Natura ed è estremamente semplice: F(da A a B) dipende dalla differenza di posizione e dalla differenza di tempo tra i due punti. In termini matematici queste due grandezze ¹⁶ possono essere espresse come (X₂-X₁) e (T₂-T₁).

Il contributo dominante a F(da A a B) si ha quando la luce si propaga con l'usuale velocità, cioè quando (X₂-X₁) è uguale a (T₂-T₁); ci si aspetterebbe che ciò dia l'intera ampiezza, ma c'è un'ampiezza anche per velocità di propagazione maggiori o minori di quella usuale. Nella lezione scorsa abbiamo visto che la luce non si propaga solo in linea retta; adesso troviamo anche che non viaggia alla velocità della luce!

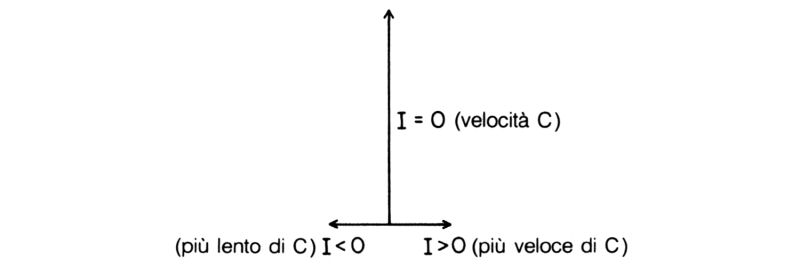
Fig. 56. Se la luce viaggia a velocità c, l'«intervallo» I è nullo e si ha un grosso contributo diretto verso le 12. Se I è maggiore di zero, si ha un piccolo contributo diretto verso le 3 e inversamente proporzionale a I; se I è minore di zero, si ha un contributo analogo ma diretto verso le 9. Dunque la luce ha ampiezza non nulla per propagarsi con velocità sia maggiore che minore di c, ma tali ampiezze si elidono a vicenda per percorsi lunghi.

Può sorprendere che alla propagazione di un fotone con velocità diverse da quella convenzionale corrispondano ampiezze non nulle. Tali ampiezze sono molto piccole paragonate a quella del contributo con velocità c, anzi si elidono quando la luce viaggia su lunghe distanze. Ma quando le distanze sono piccole, come in molti casi che vedremo, queste altre possibilità diventano essenziali e bisogna tenerne conto.

Il primo evento elementare, la prima legge fondamentale della fisica, è dunque: un fotone si propaga da un punto a un altro. Tale legge permette di spiegare tutta l'ottica, e costituisce l'intera teoria della luce! Be', non proprio tutta: ho lasciato da parte, come al solito, la polarizzazione, e anche l'interazione della luce con la materia, il che ci porta alla seconda legge.

Il secondo evento elementare fondamentale dell'elettrodinamica quantistica è il seguente: un elettrone si propaga da un punto A a un punto B dello spazio-tempo. (Per il momento lo penseremo come un elettrone semplificato, un elettrone fittizio, senza polarizzazione: ciò che i fisici chiamano particella di «spin zero». L'elettrone reale ha una specie di polarizzazione, che pero non aggiunge nulla alle idee principali e rende solo un tantino più complicate le formule).

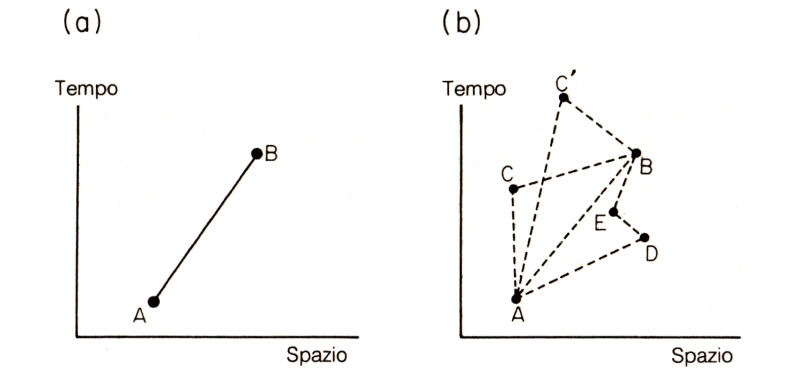
Fig. 57. L'ampiezza di probabilità che un elettrone si propaghi da un punto a un altro dello spazio-tempo sarà indicata con E(da A a B). Rappresento E(da A a B) con una linea retta tra i due punti (a), ma la si può pensare come la risultante di tante ampiezze (b), tra cui quelle per i percorsi con «due salti», in cui l'elettrone cambia direzione nei punti C o C', quelle per i percorsi con «tre salti», in cui cambia direzione in D e in E, oltre all'ampiezza relativa al percorso diretto da A a B. Nel suo viaggio nello spazio-tempo da A a B, l'elettrone può cambiare direzione un qualunque numero di volte (tra zero e infinito), e sono infiniti i punti in cui può farlo. Tutti questi contributi sono inclusi in E(da A a B).

L'ampiezza associata a questo evento base, che indicherò con E(da A a B), dipende anch'essa da (X₂-X₁) e da (T₂-T₁), nella stessa combinazione descritta nella nota 16, e inoltre da un numero che chiamerò «n», il quale, una volta determinato, permetterà ai risultati dei nostri calcoli di essere in accordo con i dati sperimentali. (Vedremo più avanti come determinare il valore di n). Purtroppo la formula è alquanto complicata e non saprei come spiegarla in termini semplici. Comunque, è interessante sapere che l'espressione dell'ampiezza per un fotone che va da A a B, F(da A a B), coincide con quella per un elettrone che va da A a B, E(da A a B), se si pone n = 0. ¹⁷

Infine, il terzo evento elementare è: un elettrone assorbe o emette un fotone (non c'è differenza tra i due casi). Questo evento lo chiamerò «accoppiamento» o «interazione».

Per distinguere nei grafici gli elettroni dai fotoni, rappresenterò un elettrone che viaggia nello spazio-tempo con un tratto rettilineo. Ogni interazione è quindi descritta come incontro tra due linee rette e una linea ondulata (fig. 58).

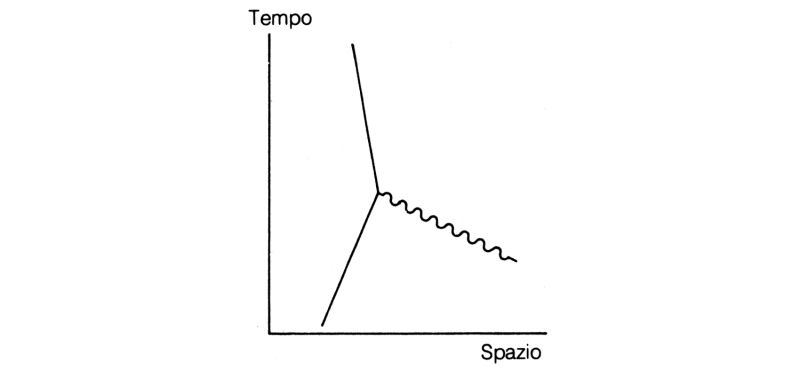
Fig. 58. Un elettrone, rappresentato dal tratto rettilineo, ha una certa ampiezza per assorbire o per emettere un fotone, rappresentato dal tratto ondulato. Poiché l'ampiezza per emissione e quella per assorbimento sono le stesse, entrambe le situazioni verranno chiamate «accoppiamento». L'ampiezza di accoppiamento è un numero, indicato con j, che vale circa —0,1 per l'elettrone. Tale numero viene a volte chiamato «carica» della particella.

L'ampiezza corrispondente a questa interazione non è espressa da una formula complicata; anzi, non dipende da nulla, è solo un numero, che io indicherò con j; esso vale circa —0,1, equivalente a una contrazione a circa un decimo e ad una rotazione di mezzo giro.¹⁸

E con questo ho detto tutto quello che c'è da dire sui tre eventi base, a parte le solite piccole complicazioni dovute alla polarizzazione, che abbiamo deciso di trascurare. Adesso dovremo affrontare il problema di combinare insieme questi tre eventi elementari per giungere a rappresentare situazioni un po' più complicate.

Quale primo esempio, calcoleremo la probabilità che due elettroni, inizialmente nei punti 1 e 2 dello spazio-tempo, finiscano nei punti 3 e 4 (fig. 59). Tale evento può verificarsi in più modi. Un primo modo corrisponde al caso in cui l'elettrone inizialmente in 1 va in 3, e a ciò va associata l'ampiezza E(da 1 a 3), ottenuta ponendo 1 e 3 nella formula di E(da A a B), mentre l'elettrone 2 va in 4, con ampiezza E(da 2 a 4). Poiché questi due «sottoeventi» devono essere concomitanti, le due frecce vanno moltiplicate tra loro per ottenere la freccia relativa a questa possibilità. Perciò l'espressione per la freccia del «primo modo» è data da E(da 1 a 3) × E(da 2 a 4).

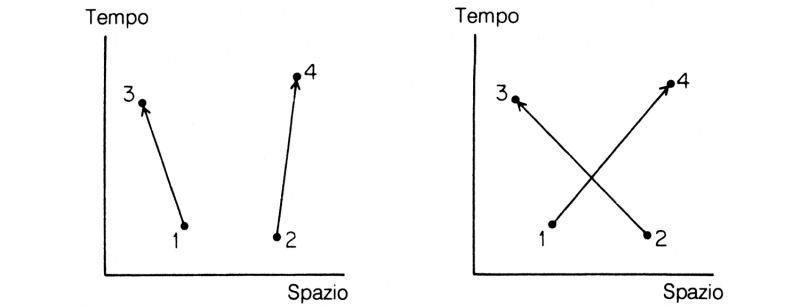
Fig. 59. Per calcolare la probabilità che due elettroni inizialmente nei punti 1 e 2 dello spazio-tempo finiscano nei punti 3 e 4, si deve calcolare, usando l'espressione di E(da A a B), la freccia per il «primo modo», in cui 1 va in 3 e 2 va in 4; poi si calcola la freccia per il «secondo modo», in cui 1 va in 4 mentre 2 va in 3 (una «intersezione»). Sommando queste frecce per il «primo» e per il «secondo modo» si ottiene una buona approssimazione della freccia finale. Ciò è vero per l'elettrone fittizio di «spin zero». Se avessimo incluso la polarizzazione dell'elettrone, avremmo dovuto sottrarre, invece che sommare, le due frecce.

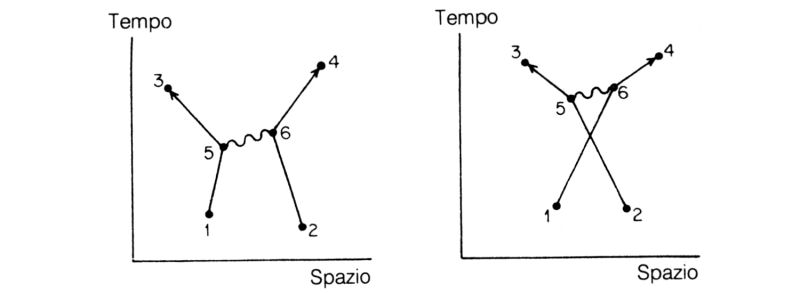
Fig. 60. Due «altri modi» in cui può verificarsi l'evento della fig. 59: in entrambi un fotone viene emesso in 5 e assorbito in 6. Queste alternative hanno condizioni finali identiche ai primi due modi: due elettroni partono e due elettroni arrivano; esse sono perciò indistinguibili dalle precedenti possibilità. Quindi, per ottenere un'approssimazione migliore della freccia risultante che descrive il fenomeno, le frecce relative a questi «altri modi» vanno sommate a quelle dei modi della fig. 59.

Il fenomeno può però avvenire anche in un secondo modo: l'elettrone in 1 va in 4, mentre quello in 2 va in 3. Anche in questo caso si hanno due «sottoeventi» concomitanti. Al «secondo modo» corrisponde perciò un'ampiezza E(da 1 a 4) × E(da 2 a 3), da sommare alla «prima» freccia.¹⁹

L'ampiezza così ottenuta costituisce una buona approssimazione per la descrizione di questo evento. Per fare un conto più esatto e in migliore accordo con i risultati sperimentali, dobbiamo considerare ancora altri modi in cui l'evento può verificarsi. Ad esempio, in corrispondenza a ciascuno dei due modi principali, un elettrone potrebbe andare prima in un altro punto a suo piacimento e lì emettere un fotone; il secondo elettrone, che nel frattempo se ne è andato in un altro punto, assorbe qui tale fotone (fig. 60). Il calcolo dell'ampiezza per il primo di questi due nuovi modi comporta il prodotto delle ampiezze relative ai seguenti passi: un elettrone va da 1 al nuovo punto 5, dove emette un fotone per poi proseguire fino a 3; l'altro elettrone va da 2 a 6, dove assorbe il fotone e poi prosegue da 6 a 4. Ricordiamoci inoltre di includere l'ampiezza per il fotone che va da 5 a 6. L'espressione matematica per l'ampiezza relativa a questo modo è dunque data da E(da 1 a 5) × j × E(da 5 a 3) × E(da 2 a 6) × j × E(da 6 a 4) × F(da 5 a 6): un bel po' di contrazioni e rotazioni! (Lascio a voi il piacere di costruire l'espressione per il caso in cui l'elettrone in 1 arriva in 4 mentre quello in 2 arriva in 3). ²⁰

Ma un momento: i punti 5 e 6 possono essere dovunque nello spazio e nel tempo — ripeto: dovunque — e per tutte queste posizioni si devono calcolare e poi sommare tra loro le frecce relative. Come vedete, sta diventando un lavoro enorme. Non che le regole siano molto difficili; è un po' come giocare a dama: le regole in sé sono semplici, ma si tratta di applicarle ripetutamente. La difficoltà del calcolo proviene dal dover mettere insieme un numero così grande di frecce. Ci vogliono quattro anni di specializzazione per imparare a fare questo conto in modo efficiente, e si tratta di un problema semplice! (Quelli troppo complicati li infiliamo direttamente in un calcolatore!).

Vorrei sottolineare un aspetto connesso con l'emissione e l'assorbimento dei fotoni: se il punto 6 è successivo al 5 si può dire che il fotone è stato emesso nel punto 5 e assorbito in 6 (fig. 61). Viceversa, se 6 è antecedente a 5, potremmo trovare preferibile dire che il fotone è stato emesso in 6 ed assorbito in 5, ma potremmo anche dire che il fotone viaggia all'indietro nel tempo!

 

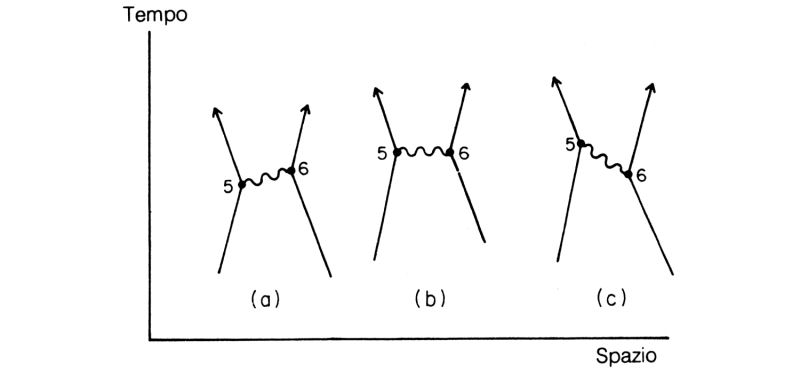
Fig. 61. Poiché la luce ha un'ampiezza non nulla per propagarsi con velocità maggiore o minore di quella convenzionale, nei tre esempi in figura i fotoni possono sempre considerarsi emessi nel punto 5 e assorbiti in 6, anche se il fotone dell'esempio (b) viene emesso allo stesso istante in cui viene assorbito, e quello dell'esempio (c) è emesso dopo essere stato assorbito — situazione che forse qualcuno preferirebbe descrivere come: fotone emesso in 6 e assorbito in 5; altrimenti il fotone deve viaggiare all'indietro nel tempo! Per quanto riguarda i calcoli (e la Natura), le due descrizioni sono assolutamente equivalenti (e possibili), per cui si preferisce semplicemente dire che un fotone viene «scambiato» e inserire le sue posizioni spaziotemporali nell'espressione di F(da A a B).

Comunque, non ci si deve preoccupare della direzione spaziotemporale in cui viaggia il fotone: è già tutto incluso nella formula che esprime F(da 5 a 6) e basta dire che è stato «scambiato» un fotone. Non è meravigliosa la semplicità della Natura? ²¹

Oltre al fotone scambiato tra 5 e 6, ne potrebbe essere scambiato un secondo, ad esempio tra i punti 7 e 8 (fig. 62). È troppo faticoso scrivere tutti i passi le cui frecce vanno moltiplicate tra loro, ma, come avrete notato, a ogni linea retta corrisponde E(da A a B), a ogni linea ondulata F(da A a B), e ad ogni interazione un fattore j. Ci sono sei E(da A a B), due F(da A a B) e quattro j, per tutti i valori possibili di 5, 6, 7 e 8! Il che significa dover moltiplicare tra loro e poi sommare miliardi di freccette!

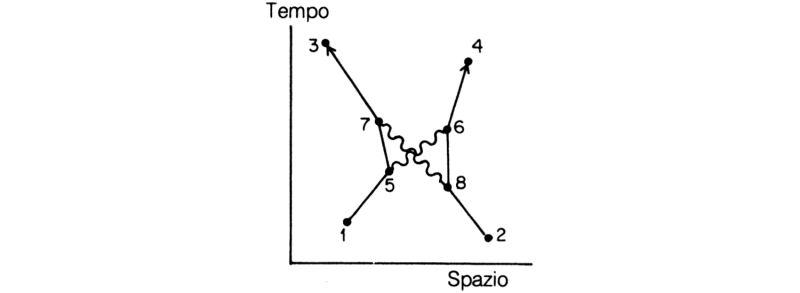
Fig. 62. Il fenomeno della fig. 59 può anche avvenire con lo scambio di due fotoni. Sono possibili moltissimi diagrammi di questo tipo (come si vedrà meglio più avanti), e uno di essi è mostrato in figura. La freccia relativa a questo modo va calcolata tenendo conto di tutte le possibili posizioni dei punti 5, 6, 7 e 8, e il conto risulta molto complesso. Poiché j risulta minore di 0,1, la lunghezza di tale freccia, che comprende quattro interazioni, è in generale inferiore a un decimillesimo delle frecce relative al «primo» e al «secondo modo» della fig. 59 che non coinvolgono j.

Insomma, calcolare l'ampiezza per questo semplice evento si direbbe proprio un'impresa disperata, ma quando si è all'università e c'è in ballo la laurea, si tiene duro e si va avanti.

Ma una speranza di successo c'è e si trova nel magico numero j. Abbiamo discusso diversi modi in cui l'evento considerato può verificarsi; ora si noti che i primi due non contengono j nel calcolo dell'ampiezza, i successivi due contengono j × j, e gli ultimi contengono j × j × j × j. Poiché j × j è minore di 0,01, la freccia per i secondi due modi è in linea di massima inferiore all'1% di quella per i primi due, mentre l'ampiezza che contiene j × j × j × j è minore dell'1% dell'1% (cioè di una parte su 10.000) di quella senza j. Se si ha abbastanza tempo a disposizione su un calcolatore, si possono calcolare le ampiezze che coinvolgono sei j (dell'ordine di una parte per milione) e uguagliare la precisione dei dati sperimentali. Ecco come si procede al calcolo di eventi semplici; e questo è tutto!

Si consideri ora un evento diverso: si comincia con un fotone e un elettrone e si finisce con un fotone e un elettrone. Tale evento può avvenire nel modo seguente: il fotone viene assorbito dall'elettrone, il quale continua a viaggiare per un po' e poi emette un nuovo fotone. Questo processo viene chiamato diffusione della luce, e nel tracciare i relativi diagrammi si devono includere alcune possibilità bizzarre (fig. 63). Ad esempio, l'elettrone può emettere il nuovo fotone prima di assorbire il vecchio (b). Oppure, possibilità ancora più strana, l'elettrone emette un fotone, viaggia all'indietro nel tempo, assorbe il vecchio fotone e poi si propaga nuovamente in avanti nel tempo (c). Il percorso di questi elettroni che viaggiano «all'indietro» può essere tanto lungo da apparire reale negli esperimenti di fisica in laboratorio. Questo comportamento è incluso nei diagrammi considerati e nell'espressione di E(da A a B).

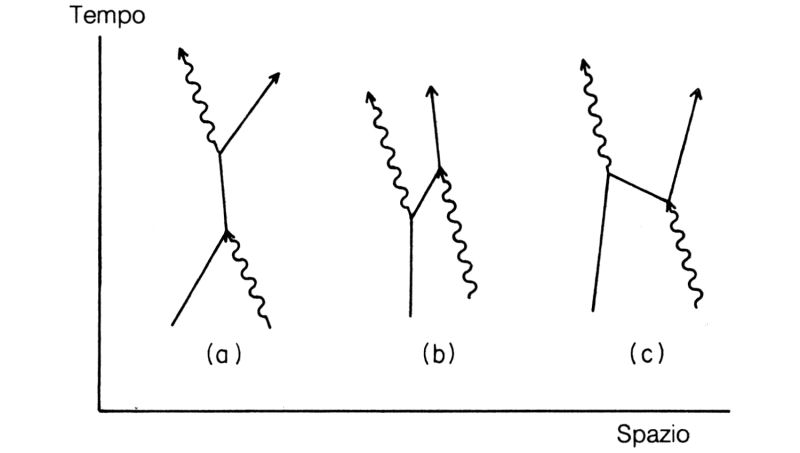
Fig. 63. La diffusione della luce consiste nell'assorbimento e nell'emissione di un fotone da parte di un elettrone. Come evidenziato in (b), questi due eventi non avvengono necessariamente in tale sequenza. L'esempio (c) mostra una possibilità strana ma reale: l'elettrone emette un fotone, poi si precipita all'indietro nel tempo ad assorbire un altro fotone e infine si propaga nuovamente in avanti nel tempo.

Dal punto di vista del tempo che avanza, gli elettroni che viaggiano «all'indietro» appaiono identici a quelli ordinari tranne che vengono attratti da essi, cioè hanno «carica positiva». (Includere gli effetti della polarizzazione renderebbe evidente perché il segno j debba essere rovesciato per gli elettroni che viaggiano all'indietro nel tempo, facendo apparire positiva la loro carica). Per questo motivo sono chiamati «positroni». I positroni sono particelle gemelle degli elettroni e sono un esempio di «antiparticella». ²²

Questa proprietà è generale. Ogni particella esistente in Natura ha un'ampiezza per muoversi all'indietro nel tempo, e perciò una corrispondente antiparticella. Se particella e antiparticella si urtano, possono annichilarsi a vicenda, dando luogo ad altre particelle. Così un elettrone e un positrone che si annichilano producono, di solito, uno o due fotoni. E i fotoni? Come si è visto prima, questi appaiono assolutamente identici quando viaggiano all'indietro nel tempo, per cui coincidono con le proprie antiparticelle. Si noti con quanta astuzia l'eccezione viene inserita nella regola!

Ora cercherò di illustrarvi come appare un elettrone che viaggia all'indietro nel tempo a chi si muove in avanti. A questo scopo dividerò il grafico della fig. 64 in tanti intervalli di tempo, da T₀ a T₁₀, tracciando una serie di linee parallele per aiutare l'occhio. Si inizi a T₀ con un elettrone in moto verso un fotone che viaggia in direzione opposta. All'istante T₃ il fotone si tramuta in due particelle: un elettrone e un positrone. Quest'ultimo non dura a lungo; dopo un po', a T₅, incontra il primo elettrone e si annichila dando luogo a un nuovo fotone. Nel frattempo, l'elettrone creato dal fotone iniziale continua il suo viaggio nello spazio-tempo.

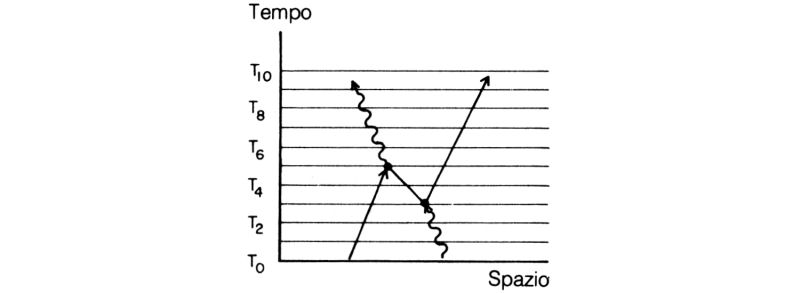
Fig. 64. L'esempio (c) della fig. 63 descritto considerando solo il moto in avanti nel tempo (come si è costretti a fare in laboratorio): da T₀ a T₃ si osservano un elettrone e un fotone che si muovono l'uno verso l'altro. All'improvviso, a T₃, il fotone si «disintegra» e al suo posto appaiono due particelle: un elettrone e un nuovo tipo di particella (chiamata «positrone»). Quest'ultima, che è un elettrone che viaggia all'indietro nel tempo, sembra muoversi verso l'elettrone iniziale (nientemeno!). A T₅, il positrone incontra questo elettrone e i due si annichilano dando luogo ad un nuovo fotone. Nel frattempo l'elettrone creato dal fotone originale continua il suo moto in avanti nel tempo. Questa successione di avvenimenti è stata osservata in laboratorio ed è automaticamente inclusa nell'espressione di E(da A a B).

Passiamo ora agli elettroni negli atomi. Per poter descrivere il comportamento di questi elettroni occorre introdurre un elemento nuovo: il nucleo, la parte pesante al centro di ciascun atomo, che contiene almeno un protone (quest'ultimo è una sorta di «vaso di Pandora» che apriremo nella prossima lezione).

Non posso spiegare in questa lezione le leggi esatte del comportamento del nucleo, che sono troppo complesse. Ma se lo si considera in quiete, se ne può assimilare il comportamento a quello di una particella la cui ampiezza per andare da un punto a un altro dello spazio-tempo è espressa dalla formula E(da A a B), ma con un valore di n molto più grande; essendo il nucleo tanto più pesante di un elettrone, si può approssimativamente affermare che esso resta di fatto nella stessa posizione spaziale mentre si sposta nel tempo.

L'atomo più semplice, chiamato idrogeno, è formato da un elettrone e da un protone. Tramite lo scambio di fotoni, il protone trattiene vicino a sé l'elettrone che gli danza intorno (fig. 65).²³

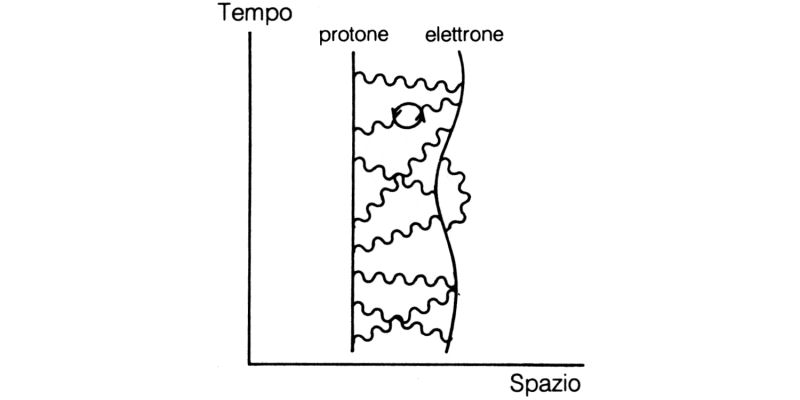
Fig. 65. Un elettrone viene mantenuto entro una certa distanza dal nucleo di un atomo dallo scambio di fotoni col protone (un «vaso di Pandora» in cui guarderemo nell'ultima lezione). Per il momento il protone viene considerato come una particella ferma. In figura è mostrato un atomo di idrogeno, che consiste in un protone e in un elettrone che si scambiano fotoni.

Naturalmente anche gli atomi che contengono più di un protone e un numero uguale di elettroni diffondono la luce (ad esempio, gli atomi dell'aria diffondono la luce solare rendendo azzurro il cielo), ma i loro diagrammi dovrebbero contenere un tale numero di linee diritte e ondulate che non ci si capirebbe più nulla!

Ora vi mostrerò un diagramma relativo alla diffusione della luce da parte dell'elettrone di un atomo di idrogeno (fig. 66). Mentre elettrone e nucleo stanno scambiandosi fotoni, arriva un fotone dall'esterno dell'atomo, urta l'elettrone e ne viene assorbito; dopodiché viene emesso un nuovo fotone. (Ci sono, al solito, anche altre possibilità da considerare, ad esempio che il nuovo fotone venga emesso prima che il vecchio sia stato assorbito). L'ampiezza totale relativa a tutti i modi in cui l'elettrone può diffondere un fotone è rappresentata da una freccia equivalente a una certa contrazione e a una certa rotazione (freccia che in seguito indicherò con «S»). Contrazione e rotazione dipendono dal nucleo e dalla disposizione degli elettroni nell'atomo, e sono differenti per sostanze differenti.

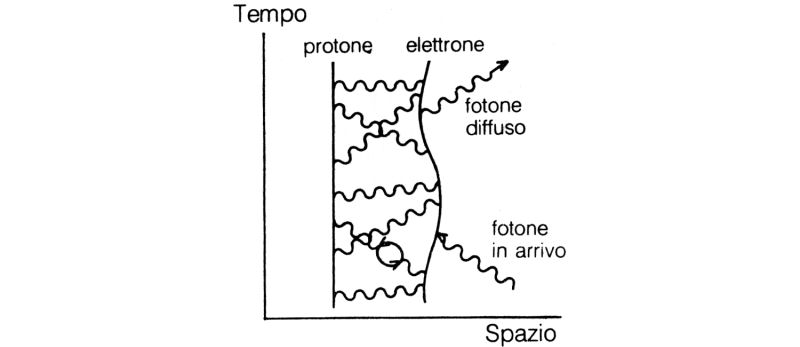
Fig. 66. La diffusione della luce da parte degli elettroni negli atomi è il fenomeno che sta alla base della riflessione parziale in una lamina di vetro. Il diagramma in figura mostra un possibile modo di diffusione in un atomo di idrogeno.

Torniamo alla riflessione parziale della luce su una lamina di vetro. Come funziona? Ho parlato di riflessione sulle superfici frontale e posteriore, ma si è trattato di una semplificazione fatta per facilitare le cose all'inizio. In realtà le superfici non hanno alcun effetto sulla luce. Il fotone incidente viene diffuso dagli elettroni all'interno del vetro, e quello che finisce nel rivelatore è un nuovo fotone. La cosa interessante è che, invece di sommare le miriadi di piccole frecce che rappresentano le ampiezze relative alla diffusione del fotone incidente da parte di tutti gli atomi del vetro, si può ottenere lo stesso risultato sommando solo due frecce, corrispondenti alla riflessione sulla «superficie frontale» e sulla «superficie posteriore». Vediamo perché.

Per discutere la riflessione su una lamina dal nuovo punto di vista, occorre prendere in considerazione la dimensione temporale. Finora, parlando della luce proveniente da una sorgente monocromatica, abbiamo usato un cronometro immaginario la cui lancetta gira durante il moto del fotone e, con la sua posizione, determina l'angolo dell'ampiezza relativa a un dato percorso. Nella formula F(da A a B), che esprime l'ampiezza perché il fotone vada da un punto A a un punto B, non si fa menzione di rotazione. Che cosa è successo al cronometro? Che fine ha fatto la rotazione?

Nella prima lezione ho considerato delle «sorgenti monocromatiche», senza ulteriori chiarimenti. Per analizzare correttamente la riflessione parziale su una lamina occorre saperne di più su queste sorgenti monocromatiche. In generale l'ampiezza per l'emissione di un fotone dalla sorgente varia nel tempo, e in particolare ciò che varia è il suo angolo. Una sorgente di luce bianca, che è una sovrapposizione di molti colori, emette fotoni in modo caotico; l'angolo dell'ampiezza varia bruscamente e irregolarmente, a sbalzi. Una sorgente monocromatica consiste invece in un dispositivo accuratamente costruito in modo che l'ampiezza per l'emissione di un fotone a un certo istante è facilmente calcolata: il suo angolo varia nel tempo con velocità costante, come quello di una lancetta di cronometro. (In effetti, questa freccia gira alla stessa velocità della lancetta del cronometro immaginario usato prima, ma in verso opposto: si veda la fig. 67).

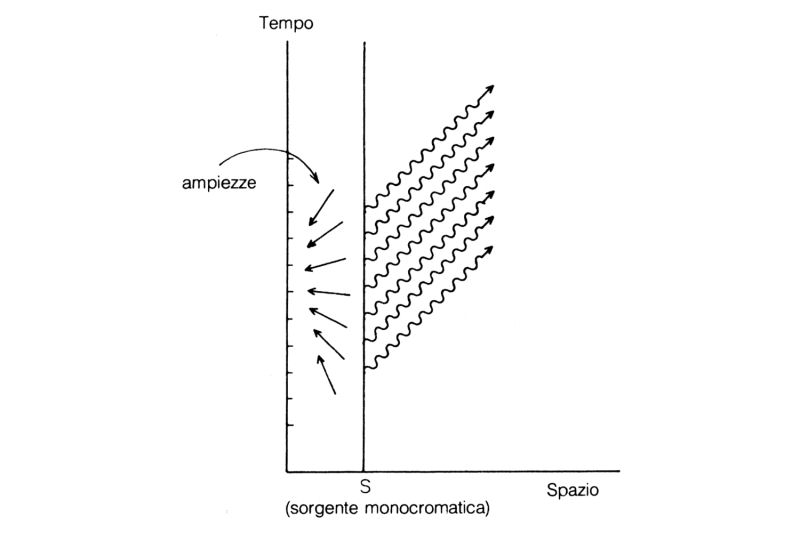
Fig. 67. Una sorgente monocromatica è un bellissimo dispositivo che emette fotoni in modo estremamente prevedibile: l'ampiezza per l'emissione di un fotone a un dato istante ruota uniformemente in senso antiorario col passare del tempo. Così l'ampiezza per l'emissione di un fotone a un istante successivo ha un angolo minore. Negli esempi seguenti si assumerà che la luce emessa dalla sorgente viaggi a velocità c, essendo grandi le distanze percorse.

La velocità di rotazione dipende dal colore della luce; la freccia per la luce blu ruota con velocità quasi doppia di quella per la luce rossa. Il «cronometro immaginario» era in realtà la sorgente monocromatica: l'angolo a cui si trova la freccia relativa a un dato percorso dipende dall'istante in cui il fotone è stato emesso dalla sorgente.

Una volta emesso il fotone, non vi è ulteriore rotazione della freccia durante il viaggio da un punto a un altro dello spazio-tempo. Sebbene l'espressione F(da A a B) contenga ampiezze per propagazione con velocità diverse da c, nel nostro esperimento la distanza tra sorgente e rivelatore è molto grande (rispetto a quelle atomiche), e quindi gli unici contributi alla lunghezza di F(da A a B) che non si elidono sono quelli che viaggiano con velocità c.

Prima di iniziare a calcolare in questo nuovo modo la riflessione parziale, è opportuno caratterizzare completamente l'evento come segue: il rivelatore in A fa uno scatto all'istante T (fig. 68 a). Suddividiamo ora la lamina di vetro in sezioni molto sottili, mettiamo sei. Come abbiamo visto nella seconda lezione, la luce è sostanzialmente riflessa dalla zona centrale di uno specchio, perché, sebbene ogni elettrone diffonda la luce in tutte le direzioni, sommando tra loro tutte le frecce relative a una sezione della lamina l'unica zona i cui contributi non si elidono è quella centrale, dove la luce arriva quasi perpendicolarmente dalla sorgente e prosegue lungo una delle due direzioni seguenti: o risale verso il rivelatore oppure va diritta attraverso il vetro. La freccia risultante per l'evento verrà quindi ottenuta sommando le frecce che rappresentano la riflessione della luce nei sei punti centrali, da X₁ a X₆, disposti verticalmente all'interno del vetro.

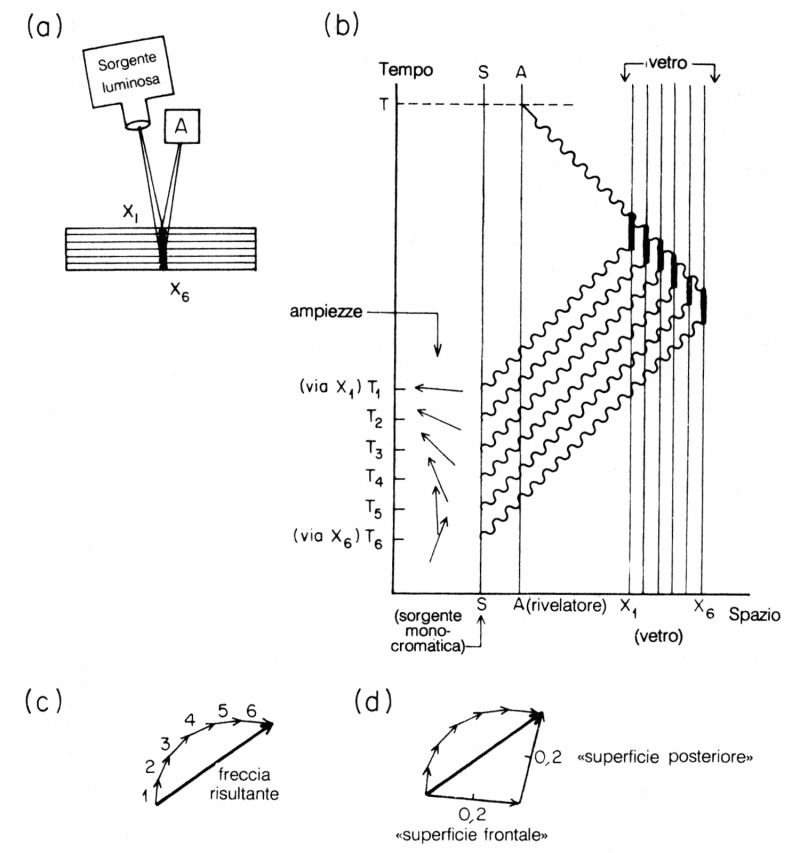
Fig. 68. Per cominciare la nostra nuova analisi della riflessione parziale, dividiamo la lamina di vetro in sezioni (sei, nell'esempio in figura) e consideriamo i possibili modi in cui la luce può andare dalla sorgente al vetro e da lì al rivelatore in A. Gli unici punti importanti della lamina, per i quali le ampiezze di diffusione non si elidono tra loro, sono al centro di ogni sezione; in (a) questi punti, da X₁ a X₆, sono mostrati nella loro collocazione fisica all'interno del vetro, mentre in (b) sono mostrati come linee verticali in un grafico spaziotemporale. Vogliamo calcolare la probabilità del seguente evento: il rivelatore in A fa uno scatto all'istante T. Nel diagramma spaziotemporale a questo evento corrisponde il punto in cui A e T si intersecano.

Ciascuno dei modi in cui tale evento può verificarsi consiste in quattro passi successivi, per cui occorre moltiplicare quattro frecce. I passi sono illustrati in (b): 1) un fotone parte dalla sorgente a un dato istante (le frecce da T₁ a T₆ rappresentano le ampiezze per l'emissione in tali istanti); 2) il fotone va dalla sorgente a uno dei punti nel vetro (le sei alternative sono disegnate come linee ondulate che salgono verso destra); 3) un elettrone in uno di detti punti diffonde il fotone (mostrato come un breve tratto verticale più spesso); 4) un nuovo fotone (la linea ondulata che sale verso sinistra) si dirige verso il rivelatore dove giunge precisamente all'istante T. Le ampiezze per i passi 2, 3 e 4 sono identiche per tutte le alternative, solo quelle per il passo 1 sono differenti: un fotone diffuso internamente al vetro, ad esempio in X₂, deve partire dalla sorgente a T₂, prima di un fotone diffuso da un elettrone alla superficie del vetro, in X₁.

Dopo aver moltiplicato tra loro le quattro frecce relative a ciascuna alternativa, si ottengono le frecce mostrate in (c), più corte di quelle in (b) e ruotate di 90° in base alle caratteristiche della diffusione della luce da parte degli elettroni del vetro. Sommando nell'ordine queste frecce si ottiene un arco di cerchio, la cui corda è la freccia risultante. La stessa freccia finale è ottenibile disegnando due frecce radiali, mostrate in (d), e «sottraendo» l'una all'altra, cioè girando la freccia «frontale» nella direzione opposta prima di sommarla a quella «posteriore». Questa scorciatoia è stata usata come semplificazione nella prima lezione.

E adesso calcoliamo le frecce relative a questi sei percorsi, ciascuno dei quali comporta quattro passi, ossia quattro frecce da moltiplicare.

1. un fotone viene emesso dalla sorgente a un dato istante.
2. il fotone si propaga dalla sorgente a uno dei punti nel vetro.
3. il fotone è diffuso da un elettrone in quel punto.
4. un nuovo fotone risale fino al rivelatore.

Alle ampiezze relative ai passi 2 e 4 (propagazione di un fotone) non faremo corrispondere alcuna contrazione né alcuna rotazione, perché si può assumere che nel percorso tra la sorgente e il vetro o tra questo e il rivelatore il fascio di luce non si attenui né si allarghi. L'ampiezza per il terzo passo (diffusione di un fotone da parte di un elettrone) vale S, cioè una certa contrazione e una certa rotazione ed è la stessa in ogni punto del vetro. (Come ho detto prima, questo valore di S dipende dal materiale; per il vetro la rotazione risulta di 90°). In conclusione, delle quattro frecce da moltiplicare l'unica a cambiare da un percorso all'altro è quella relativa al primo passo, cioè l'ampiezza per l'emissione di un fotone dalla sorgente a un certo istante.

L'istante in cui un fotone deve essere emesso per arrivare nel rivelatore A al tempo T (fig. 68 b) non è lo stesso per tutti i percorsi. Il fotone che rimbalza in X₂ deve venire emesso leggermente prima del fotone che rimbalza in X₁, perché il suo percorso è più lungo. Dunque la freccia relativa a T₂ sarà ruotata un po' di più di quella a T₁, perché l'ampiezza per l'emissione di un fotone da parte di una sorgente monocromatica ruota in senso antiorario col passare del tempo. Lo stesso vale per le altre frecce fino a T₆: hanno tutte lunghezza identica ma sono ruotate di angoli differenti, puntano cioè, in direzioni differenti, in quanto corrispondono a fotoni emessi dalla sorgente in istanti differenti.

Contraendo la freccia relativa a T₁ del fattore prescritto dai passi 2, 3 e 4, e ruotandola dei 90° prescritti dal passo 3, si ottiene la freccia 1 (fig. 68 c). Con lo stesso procedimento si trovano le frecce da 2 a 6. Queste sei frecce hanno tutte la stessa lunghezza (contratta) e formano tra loro esattamente gli stessi angoli delle frecce relative agli istanti di emissione.

Ora dobbiamo sommarle. Congiungendole nell'ordine, da 1 a 6, si ottiene una specie di arco, o parte di un cerchio, la cui corda è appunto la freccia finale. Poiché maggior spessore di vetro significa più sezioni, cioè più frecce e perciò una porzione maggiore di cerchio, la lunghezza della corda aumenta con lo spessore del vetro finché si arriva a un semicerchio e a una freccia finale pari al diametro. Poi la sua lunghezza diminuisce con l'aumentare dello spessore, e quando il cerchio è completo si inizia un nuovo ciclo. Il quadrato della lunghezza della freccia finale dà la probabilità dell'evento e varia ciclicamente da zero al 16%.

Un trucco matematico permette di ottenere la stessa risposta in modo diverso (fig. 68 d): se dal centro del «cerchio» tracciamo due frecce, una fino alla coda della freccia 1 e l'altra alla punta della 6, otteniamo due raggi. Se la freccia radiale che va dal centro alla coda della 1 viene ruotata di 180° («cambiata di segno») e sommata all'altra freccia radiale, si ottiene la stessa freccia finale! Questo è quanto avevo fatto nella prima lezione: i due raggi del cerchio sono le frecce che rappresentavano la riflessione sulle superfici «frontale» e «posteriore». Ciascuna di esse ha la famosa lunghezza 0,2. ²⁴

Possiamo quindi ottenere la risposta corretta per la probabilità di riflessione parziale immaginando che tutta la riflessione avvenga solo sulle superfici frontale e posteriore (il che è falso). In questa analisi più intuitiva le frecce relative alla «superficie frontale» e alla «superficie posteriore» sono costruzioni fittizie che permettono di ottenere la risposta esatta, mentre l'analisi discussa adesso, usando un diagramma spaziotemporale dove le varie frecce formano un arco di cerchio, costituisce una rappresentazione più accurata di ciò che succede nella realtà: la riflessione parziale è dovuta alla diffusione della luce da parte degli elettroni interni al vetro.

Cosa accade, invece, alla luce che attraversa il vetro? Anzitutto c'è da considerare il percorso in cui il fotone attraversa il vetro senza interagire con alcun elettrone, e la relativa ampiezza (fig. 69 a).

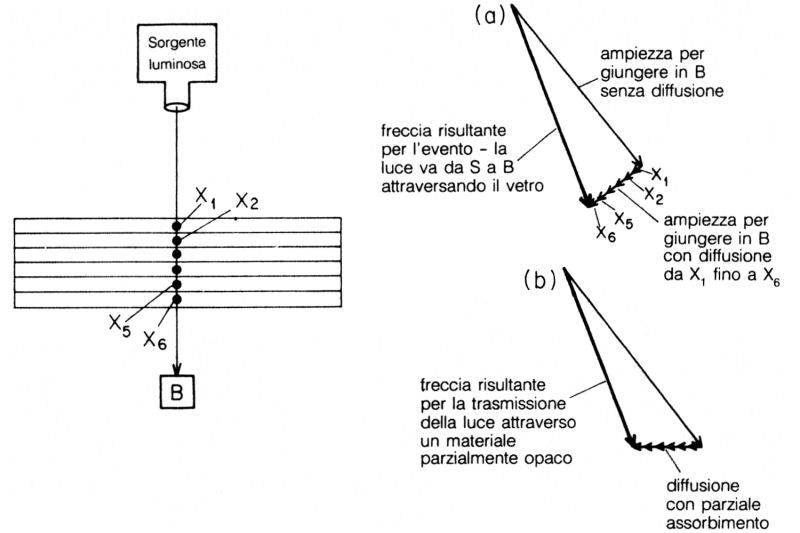
Fig. 69. Nella trasmissione della luce attraverso una lamina di vetro, fino al rivelatore in B, l'ampiezza dominante viene dalla propagazione senza diffusione da parte degli elettroni del vetro, come illustrato in (a). A questa freccia occorre aggiungere quelle più piccole corrispondenti alla diffusione da parte delle singole sezioni, rappresentate dai punti da X₁ a X₆. Queste sei frecce hanno tutte la stessa lunghezza, perché l'ampiezza di diffusione è la stessa in tutti i punti del vetro, e la stessa direzione, perché la lunghezza dei vari percorsi dalla sorgente al rivelatore in B è la stessa per tutti i punti X. Sommando queste frecce più piccole alla principale, si trova la freccia finale per la trasmissione della luce attraverso il vetro. Essa risulta più ruotata di quanto lo sarebbe se la luce si propagasse senza diffusione. Per questa ragione si ha l'impressione che la luce impieghi più tempo a viaggiare attraverso il vetro che attraverso il vuoto o l'aria. La rotazione della freccia risultante causata dagli elettroni del materiale è chiamata «indice di rifrazione».

Nei materiali trasparenti le frecce più piccole sono ad angolo retto rispetto alla principale (in realtà, includendo gli effetti della diffusione multipla, si vede che esse formano un trailo di curva così da evitare che la freccia finale risulti più lunga della principale: la Natura ha disposto le cose in modo che non esca mai più luce di quanta ne entri). Nei materiali parzialmente opachi, che assorbono leggermente la luce, le frecce secondarie sono inclinate verso la principale, dando luogo a una freccia risultante sensibilmente più corta, come mostrato in (b). La minore lunghezza di tale freccia rappresenta la ridotta probabilità di trasmissione di un fotone attraverso un materiale parzialmente opaco.

Questa costituisce la freccia più rilevante in termini di lunghezza. Ma ci sono altri sei modi in cui un fotone può giungere nel rivelatore sotto il vetro: il fotone emesso può urtare un elettrone in X₁ e il fotone diffuso finire in B, oppure l'urto può avvenire in X₂ e così via. Queste sei frecce hanno la stessa lunghezza di quelle che formavano l'arco di cerchio dell'esempio precedente, essendo tale lunghezza determinata ancora dall'ampiezza S relativa alla diffusione di un fotone da parte di un elettrone del vetro. Ma questa volta sono rivolte tutte e sei nella stessa direzione, perché i sei percorsi in cui si verifica un unico urto hanno tutti la stessa lunghezza. Per sostanze trasparenti, quali il vetro, la direzione delle frecce secondarie forma un angolo retto con la freccia principale. Sommando tali frecce, si ottiene una freccia risultante che ha la stessa lunghezza di quella principale ma è ruotata in una direzione leggermente diversa. Più spesso è il vetro più frecce secondarie vi sono e maggiore è la rotazione della freccia risultante. Su questo si basa appunto il funzionamento di una lente convergente: inserendo un opportuno spessore di vetro lungo percorsi più corti si ottengono per tutti i percorsi frecce che puntano nella stessa direzione.

Lo stesso effetto si avrebbe se i fotoni andassero più lentamente nel vetro che nell'aria: anche questo darebbe luogo a una maggior rotazione della freccia finale. Ecco perché, come ho detto prima, si ha l'impressione che la luce vada più lenta nel vetro, o nell'acqua, che nell'aria. In realtà, il «rallentamento» della luce non è altro che la maggior rotazione della freccia finale provocata dalla diffusione da parte degli atomi del vetro o dell'acqua. Il grado di rotazione in più della freccia finale, dovuto all'attraversamento di un materiale, viene detto «indice di rifrazione». ²⁵

Per le sostanze che assorbono la luce, le frecce secondarie formano con quella principale un angolo inferiore ai 90° (fig. 69 b). Ne consegue che la freccia risultante è più corta di quella principale, per cui la probabilità che un fotone attraversi un vetro opaco è minore della probabilità che attraversi un vetro trasparente.

In questo modo, a partire da soli tre eventi base, vengono spiegati tutti gli aspetti dei fenomeni dei quali si è parlato nelle prime due lezioni (la riflessione parziale della luce con ampiezza 0,2, il suo «rallentamento» nell'acqua e nel vetro, e così via). Gli stessi eventi elementari permettono altresì di spiegare tutti, o quasi, gli altri fenomeni.

Che l'enorme varietà della Natura sia il risultato di una monotona ripetizione dei tre eventi base in varie combinazioni non è un'idea facile da accettare. Ma è proprio così. Proverò a dare un'idea di come ha luogo tale varietà.

Inizierò dai fotoni (fig. 70).

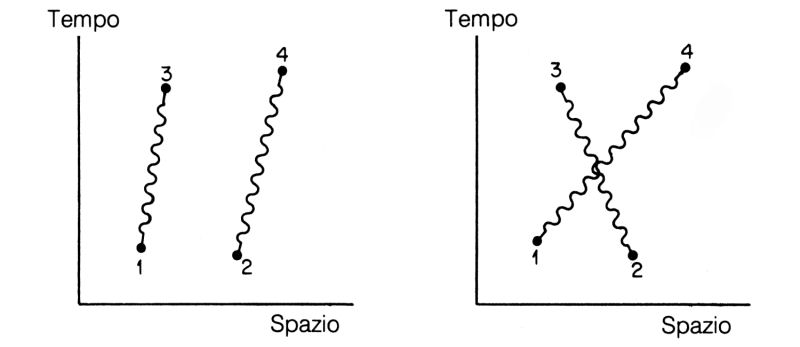
Fig. 70. Due fotoni nei punti 1 e 2 dello spazio-tempo hanno un'ampiezza per giungere nei punti 3 e 4 che può essere approssimata considerando i due modi principali in cui il fenomeno può accadere: F(da 1 a 3) × F(da 2 a 4) e F(da 1 a 4) × F(da 2 a 3). A seconda della posizione relativa dei punti 1, 2, 3 e 4, si producono diversi gradi di interferenza.

Qual è la probabilità che due fotoni dai punti 1 e 2 dello spazio-tempo arrivino in due rivelatori nei punti 3 e 4? Per questo fenomeno vi sono due modi principali, ciascuno dei quali dipende dal verificarsi concomitante di due fatti: i due fotoni possono andare direttamente, con ampiezza F(da 1 a 3) × F(da 2 a 4), oppure possono «incrociarsi», con ampiezza F(da 1 a 4) × F(da 2 a 3). Le due ampiezze vanno ora sommate e ciò produce interferenza (come si è visto nella seconda lezione), con conseguente variazione della lunghezza della freccia finale, in dipendenza della posizione relativa dei punti nello spazio-tempo.

Cosa succede se si portano a coincidere nello spazio-tempo i punti 3 e 4? (fig. 71). Supponiamo che entrambi i fotoni giungano nel punto 3, e vediamo come ciò influenzi le probabilità dell'evento. In questo caso F(da 1 a 3) × F(da 2 a 3) e F(da 2 a 3) × F(da 1 a 3) risultano ampiezze identiche; la loro somma ha quindi lunghezza doppia di quella di ciascuna, e il quadrato della freccia finale è quattro volte quello di ciascuna freccia separatamente. Le due frecce, essendo identiche, sono sempre «allineate». In altre parole, l'interferenza non fluttua al variare della separazione relativa tra i punti 1 e 2: è sempre positiva. Se non si tenesse presente questa interferenza sempre positiva tra i due fotoni, si sarebbe portati a pensare che in media si ha probabilità doppia. Invece la probabilità è sempre quadrupla. Se sono coinvolti parecchi fotoni la probabilità aumenta ulteriormente, rispetto a quanto ci si aspetterebbe.

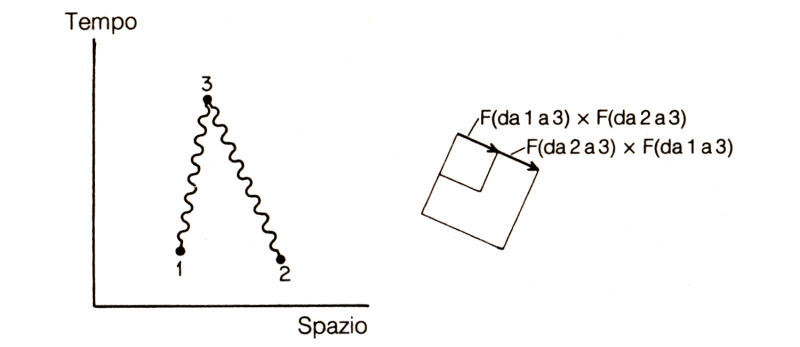
Fig. 71. Portando a coincidere i punti 3 e 4, le due frecce F(da 1 a 3) × F(da 2 a 3) e F(da 2 a 3) × F(da 1 a 3) diventano identiche in lunghezza e in direzione. Quando le si somma, essendo sempre «allineate», danno luogo a una freccia lunga il doppio di ciascuna di esse, il cui quadrato è quindi quattro volte maggiore. Pertanto i fotoni tendono a trovarsi nello stesso punto spaziotemporale. L'effetto è ancora più amplificato se sono coinvolti più fotoni. Questa proprietà sta alla base del funzionamento del laser.

Questo fatto ha numerose conseguenze pratiche. In linguaggio tecnico si dice che i fotoni tendono a stare nello stesso «stato», termine che indica in che modo l'ampiezza per trovare un fotone dipenda dalla posizione. La probabilità che un atomo emetta un fotone aumenta se è già presente qualche altro fotone (in uno stato nel quale l'atomo lo può emettere). Einstein scoprì questo fenomeno di «emissione stimolata» formulando il modello quantistico della luce basato sui fotoni. Il laser funziona sulla base di tale principio.

Ripetendo l'analogo conto per il nostro elettrone fittizio di spin zero, si troverebbe lo stesso comportamento. Ma con gli elettroni del mondo reale, che hanno polarizzazione, accade qualcosa di completamente diverso: le due frecce E(da 1 a 3) × E(da 2 a 4) e E(da 1 a 4) × E(da 2 a 3) vanno sottratte fra loro, cioè una di esse viene ruotata di 180" prima della somma. Se i punti 3 e 4 coincidono le due frecce hanno stessa lunghezza e direzione, per cui nella sottrazione si elidono (fig. 72). Ciò significa che, a differenza dei fotoni, gli elettroni non amano trovarsi nello stesso posto e si evitano l'un l'altro come la peste: due elettroni con la stessa polarizzazione non potranno mai stare nello stesso punto dello spazio-tempo. Tale proprietà è nota come «principio di esclusione».

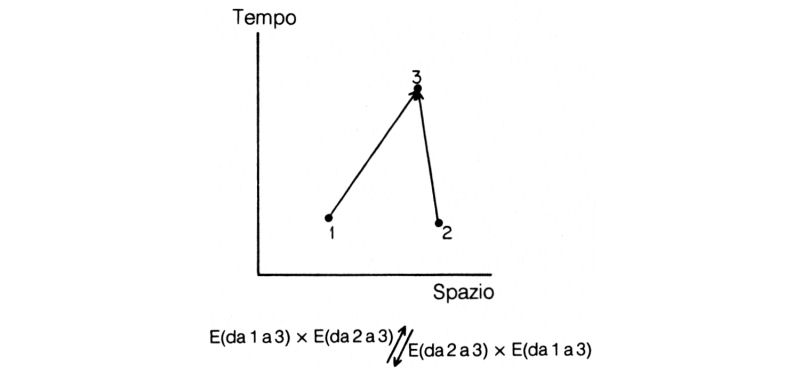
Fig. 72. Se due elettroni (con la stessa polarizzazione) tentano di andare nello stesso punto dello spazio-tempo, si ha sempre interferenza distruttiva per effetto della polarizzazione: le due frecce identiche E(da 1 a 3) × E(da 2 a 3) e E(da 2 a 3) × E(da 1 a 3) si sottraggono e si ottiene una freccia finale nulla. L'avversione degli elettroni a occupare la stessa posizione spaziotemporale viene chiamata «principio di esclusione» ed è la ragione della grande varietà degli atomi nell'universo.

Questo principio sta alla base dell'enorme varietà delle proprietà chimiche degli atomi. Un protone che scambia fotoni con un elettrone che gli danza intorno è chiamato atomo di idrogeno. Due protoni in uno stesso nucleo che scambiano fotoni con due elettroni di polarizzazione opposta vengono chiamati atomo di elio. I chimici hanno un loro modo speciale, e complicato, di contare: invece di dire «uno, due, tre, quattro, cinque protoni» dicono: «idrogeno, elio, litio, berillio, boro».

Vi sono solo due stati di polarizzazione possibili per l'elettrone, per cui in un atomo con tre protoni che scambiano fotoni con tre elettroni (situazione chiamata atomo di litio) il terzo elettrone si trova più lontano dal nucleo dei primi due (che si sono presi tutto lo spazio più vicino), e scambia meno fotoni. Perciò, sotto l'effetto di fotoni provenienti da altri atomi, esso si stacca con facilità dal proprio nucleo. Quando gli atomi di litio sono molti e vicini tra loro, questo terzo elettrone viene perduto facilmente e insieme con gli altri elettroni perduti forma un mare di elettroni fluttuante tra un atomo e l'altro e pronto a reagire a qualunque forza elettrica anche piccola (fotoni), producendo una corrente di elettroni: questa è la descrizione del metallo litio, buon conduttore elettrico. Gli atomi di idrogeno e quelli di elio non cedono i loro elettroni ad altri atomi, e sono «isolanti».

Tutti gli atomi, più di un centinaio di tipi diversi, sono fatti da un certo numero di protoni che scambiano fotoni con un egual numero di elettroni. Essi si dispongono secondo configurazioni complesse che determinano un'enorme gamma di proprietà: alcuni materiali sono metalli, altri isolanti; alcuni sono gassosi, altri cristallini; vi sono materiali morbidi e materiali duri, sostanze colorate e sostanze trasparenti; una meravigliosa ed entusiasmante cornucopia di varietà dovuta al principio di esclusione e alla ininterrotta ripetizione di tre semplicissimi eventi: F(da A a B), E(da A a B) e j. (Se gli elettroni reali non avessero polarizzazione, tutti gli atomi avrebbero proprietà molto simili: gli elettroni si addenserebbero insieme, vicini al nucleo del proprio atomo, e non sarebbero attratti facilmente dagli altri atomi per dare luogo a reazioni chimiche).

Vi chiederete come è possibile che tre eventi così semplici portino a un mondo così complesso. Il fatto è che i fenomeni che vediamo intorno a noi sono il risultato del complicatissimo intrecciarsi di un immenso numero di scambi e di interferenze di fotoni. La conoscenza dei tre eventi elementari costituisce solo un primo piccolissimo passo nello studio di qualunque fenomeno reale, dove gli scambi di fotoni sono tali e tanti da rendere impossibile ogni tentativo di calcolo; occorre rendersi conto tramite l'esperienza di quali siano le possibilità dominanti. Perciò si introducono grandezze quali «indice di rifrazione», «compressibilità», «valenza», che permettono di fare calcoli approssimati trascurando un'enorme quantità di dettagli. È un po' come conoscere solo le regole del gioco degli scacchi, che sono semplici e fondamentali, rispetto al saper giocare bene, che significa comprendere l'importanza di ogni posizione e la natura delle varie situazioni, ed è molto più difficile e complesso.

I settori della fisica che cercano di scoprire come mai il ferro (che ha 26 protoni) è magnetico mentre il rame (che ne ha 29) non lo è, o perché un gas è trasparente e un altro no, sono chiamati «fisica dello stato solido» o «fisica dello stato liquido», o semplicemente «vera fisica». Il settore che ha trovato quei tre piccoli eventi semplici (la parte più facile) viene chiamato «fisica fondamentale», nome di cui ci siamo impadroniti per mettere a disagio gli altri fisici! I problemi oggi più interessanti, e certamente più rilevanti da un punto di vista pratico, sono ovviamente quelli dello stato solido. Ma è stato detto che non c'è niente di più pratico di una buona teoria, e l'elettrodinamica quantistica è decisamente una buona teoria!

Per finire, torniamo al numero 1,00115965221, così scrupolosamente calcolato e misurato, come vi ho detto nella prima lezione. Questo numero rappresenta la risposta di un elettrone a un campo magnetico esterno, ed è chiamato «momento magnetico». Le leggi per calcolarlo furono discusse per la prima volta da Dirac, il quale, in base all'espressione di E(da A a B), ottenne un risultato molto semplice che, in opportune unità, si può porre uguale a 1. A questo calcolo approssimato del momento magnetico dell'elettrone corrisponde un diagramma molto semplice: nell'andare da un punto a un altro dello spazio-tempo un elettrone interagisce con un fotone dovuto a un magnete (fig. 73).

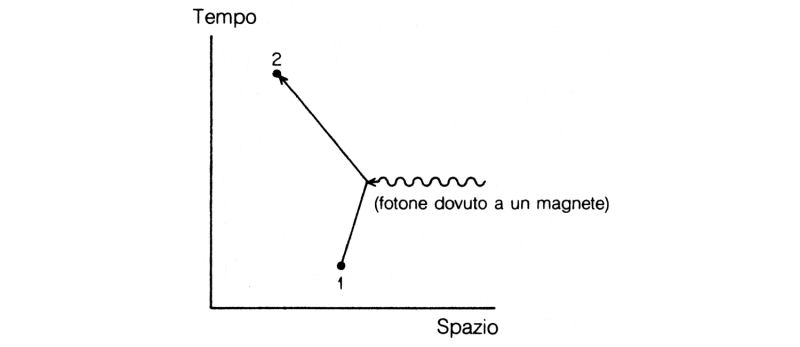
Fig. 73. Il diagramma che rappresenta il calcolo di Dirac del momento magnetico dell'elettrone è molto semplice. Il risultato dei conto rappresentato da questo diagramma verrà posto uguale a 1.

In seguito a esperimenti più precisi si trovo che il valore sperimentale non è esattamente 1, ma leggermente maggiore, vicino a 1,001116. Il valore teorico della correzione venne calcolato per la prima volta nel 1948 da Schwinger, che ottenne j × j diviso 2π prendendo in considerazione un secondo modo in cui l'elettrone può andare da un punto a un altro: invece di andarvi direttamente, l'elettrone si propaga per un tratto, poi all'improvviso emette un fotone e infine (orrore!) assorbe il fotone da lui stesso emesso (fig. 74): comportamento forse «immorale», ma assolutamente reale! Per calcolare l'ampiezza per questa seconda possibilità, si deve considerare una freccia per ogni punto dello spazio-tempo in cui il fotone può essere emesso e per ogni punto in cui può essere assorbito. Perciò l'espressione conterrà, come fattori moltiplicativi, due termini E(da A a B), un termine F(da A a B) e due termini j in più. Gli studenti di fisica imparano come fare questo semplice conto nel corso introduttivo di elettrodinamica quantistica al secondo anno di specializzazione.

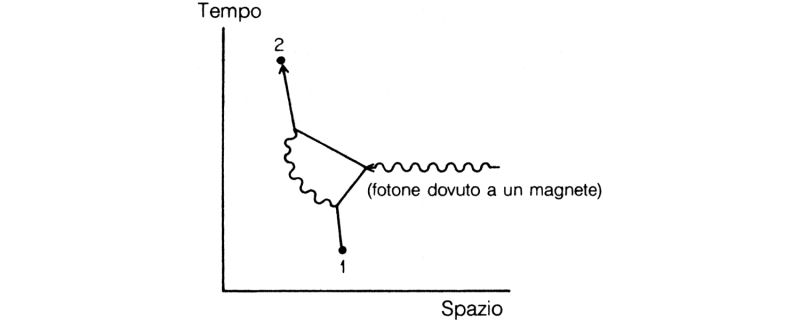
Fig. 74. Gli esperimenti di laboratorio mostrano che il valore reale del momento magnetico dell'elettrone non è 1, ma è leggermente maggiore. Ciò succede perché vi sono altre possibilità: ad esempio, l'elettrone può emettere un fotone e poi riassorbirlo, il che richiede due E(da A a B), una F(da A a B) e due j in più. La correzione che tiene conto di questa possibilità fu calcolata da Schwinger, che trovò j × j diviso 2π. Questa alternativa è sperimentalmente indistinguibile dal modo discusso prima, in cui l'elettrone va dal punto 1 al punto 2; pertanto le frecce per le due possibilità vanno sommate e si ha interferenza.

Ma non basta: il comportamento di un elettrone in campo magnetico è stato misurato così accuratamente che nel calcolo teorico si devono prendere in considerazione ancora altre possibilità, ad esempio tutti i modi in cui l'elettrone va da un punto a un altro con quattro ulteriori interazioni (fig. 75). Ci sono tre modi in cui l'elettrone può emettere e riassorbire due fotoni. C'è inoltre una nuova possibilità interessante, mostrata sulla destra della fig. 75: l'elettrone emette un fotone che si trasforma in una coppia elettrone-positrone, i quali (con buona pace delle vostre obiezioni «morali») successivamente si annichilano tra loro, dando luogo a un nuovo fotone che infine viene riassorbito dall'elettrone iniziale. Anche queste sono eventualità di cui tener conto!

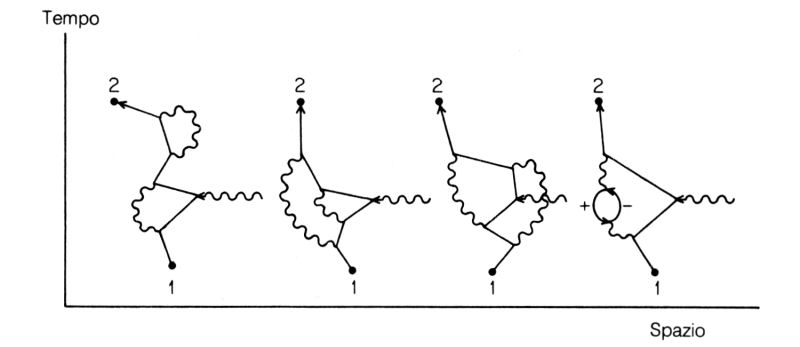
Fig. 75. Gli esperimenti di laboratorio sono diventati così accurati che si sono dovute prendere in considerazione anche alternative che comportano quattro interazioni in più (in tutti i possibili punti nello spazio-tempo). Alcune di queste alternative sono mostrate in figura: quella sulla destra riguarda un fotone che si disintegra in una coppia elettrone-positrone (come descritto alla fig. 64), i quali a loro volta si annichilano producendo un nuovo fotone che infine viene assorbito dall'elettrone.

Ci sono voluti due anni perché due gruppi «indipendenti» di fisici completassero il calcolo di quest'ultimo termine, e poi un altro anno per accorgersi che nel conto c'era un errore. Il valore misurato sperimentalmente risultava leggermente diverso da quello calcolato, e sembrò per un certo periodo che per la prima volta la teoria non fosse in accordo con gli esperimenti; invece si trattava di un semplice errore di aritmetica. Com'è possibile che due gruppi «indipendenti» facciano lo stesso errore? Il fatto è che verso la fine del calcolo i due gruppi confrontarono i propri appunti ed eliminarono le differenze tra i conti. Insomma, erano indipendenti per modo di dire.

L'ampiezza con sei j in più comporta il calcolo di un numero di modi ancora maggiore; alcuni sono disegnati alla fig. 76. Ci sono voluti venti anni per calcolare con questo livello di precisione il valore del momento magnetico dell'elettrone. Nel frattempo gli esperimenti continuavano, diventando più accurati e permettendo di aggiungere nuove cifre al valore sperimentale, che continuava ad andare d'accordo con quello teorico.

Per fare questo tipo di calcoli occorre dunque disegnare i relativi diagrammi, scrivere a che cosa equivalgono matematicamente e sommare le corrispondenti ampiezze: un procedimento molto lineare, da «ricetta di cucina».

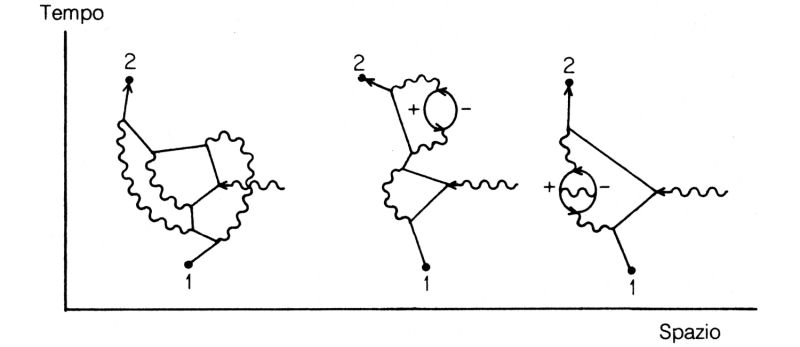
Fig. 76. Si stanno portando a termine i conti per rendere ancora più accurato il valore teorico del momento magnetico dell'elettrone. Il contributo successivo all'ampiezza, dovuto alle alternative con sei interazioni in più, comporta il calcolo di qualcosa come 10.000 diagrammi (ciascuno contenente 500 termini), tre dei quali vengono qui mostrati in figura. Nel 1983 il valore teorico era 1,00115965246, con un'incertezza di circa 20 sulle ultime due cifre, mentre il valore sperimentale era 1,00115965221, con un'incertezza di circa 4 sull'ultima cifra. Per avere un'idea di tale precisione, è come se la distanza tra New York e Los Angeles, di quasi 5.000 chilometri, fosse misurata con l'approssimazione di un capello umano.

Possiamo quindi farlo fare a una macchina. Con i fenomenali calcolatori di cui disponiamo oggi è stato iniziato il conto del termine con otto j in più. Attualmente il valore teorico è 1,00115965246, mentre quello sperimentale è 1,00115965221 con un'incertezza di più o meno quattro sull'ultima cifra decimale. Anche per il valore teorico c'è un'incertezza in parte dovuta all'arrotondamento dei numeri da parte del calcolatore, che produce un'indeterminazione di circa quattro sull'ultima cifra, ma la parte principale (circa 20) è dovuta alla imprecisa conoscenza del valore di j. Questo termine con otto j in più comporta il calcolo di circa diecimila diagrammi, ciascuno comprendente circa cinquecento termini: un conto davvero formidabile, e attualmente in corso.

Sono sicuro che fra alcuni anni il valore teorico e quello sperimentale del momento magnetico dell'elettrone saranno noti con precisione ancora maggiore. Naturalmente non so se i due valori saranno ancora in accordo tra loro. Questo non lo si può mai dire finché non viene fatto il conto e compiuto l'esperimento.

Siamo così tornati al punto da cui eravamo partiti. Avevo parlato di questo numero nella mia prima lezione per «fare colpo»; ora invece spero vi sia chiaro che cosa esso significhi: questo numero rappresenta l'estremo grado di accuratezza con cui abbiamo verificato e continuiamo a verificare l'esattezza della strana teoria dell'elettrodinamica quantistica.

In queste lezioni mi sono spesso divertito a far vedere come l'acquisizione di una teoria così precisa sia stata pagata con una erosione del comune buon senso e con la forzata accettazione di comportamenti molto bizzarri: l'aumento e la soppressione delle probabilità, la riflessione della luce in tutti i punti di uno specchio, la sua propagazione lungo percorsi che non sono linee rette, fotoni che si propagano con velocità maggiore o minore di quella convenzionale per la luce, elettroni che viaggiano all'indietro nel tempo, fotoni che scompaiono trasformandosi in coppie elettrone-positrone, e così via. Tutto ciò è necessario se si vuole capire quale sia il reale comportamento della Natura sotto la superficie di quasi tutti i fenomeni che vediamo intorno a noi.

Tranne che per il dettaglio tecnico della polarizzazione, ho descritto lo schema nel quale noi inquadriamo tutti questi fenomeni. Determiniamo le ampiezze per ogni modo in cui un evento può verificarsi e poi le sommiamo, laddove in circostanze ordinarie ci si sarebbe aspettati di sommare le probabilità; analogamente moltiplichiamo ampiezze, quando ci si sarebbe aspettati di moltiplicare probabilità. Pensare a qualunque fenomeno in termini di ampiezze può, all'inizio, causare qualche difficoltà dovuta al loro carattere astratto, ma dopo un po' ci si abitua alle stranezze di questo linguaggio. Alla base di un grandissimo numero di fenomeni quotidiani vi sono solo tre eventi fondamentali, uno dei quali è dato da un semplice numero, j, mentre gli altri due sono descritti dalle funzioni F(da A a B) e E(da A a B), molto simili tra loro. Da questi semplicissimi eventi elementari seguono tutte le altre leggi della fisica.

Ma prima di terminare questa lezione voglio fare alcune considerazioni. Per cogliere lo spirito e la fisionomia dell'elettrodinamica quantistica non è necessario includere la polarizzazione. Ma so che voi vi sentirete più tranquilli se vi dirò qualcosa anche su questo argomento. Orbene, i fotoni si presentano in quattro varietà differenti, chiamate polarizzazioni, e connesse da un punto di vista geometrico alle varie direzioni dello spazio-tempo. Ci sono cioè fotoni polarizzati lungo le direzioni X, Y, Z e T. (Avrete forse sentito dire che la luce ha solo due stati di polarizzazione; ad esempio, un fotone che viaggia lungo la direzione Z può essere polarizzato solo lungo le direzioni ortogonali, vale a dire X e Y. In situazioni in cui il fotone percorre lunghe distanze e sembra muoversi con la solita velocità della luce, le ampiezze relative alle polarizzazioni lungo Z e T, come avrete facilmente indovinato, si elidono esattamente tra loro. Ma per i fotoni virtuali, quali quelli scambiati tra un protone e un elettrone in un atomo, è proprio la componente T ad essere la più importante).

Analogamente un elettrone può trovarsi in uno tra quattro possibili stati, pure connessi alla geometria ma in modo alquanto più sottile. Chiamiamoli stati 1, 2, 3 e 4. Il calcolo dell'ampiezza per un elettrone che si propaga da un punto A a un punto B dello spazio-tempo diventa ora un po' più complesso, perché possiamo fare domande come: «Qual è l'ampiezza perché un elettrone partito dal punto A nello stato 2 arrivi nel punto B nello stato 3?». Le sedici possibili combinazioni, dovute ai quattro stati da cui l'elettrone può partire da A e ai quattro in cui può arrivare in B, sono correlate in modo semplice alla già vista formula per E(da A a B).

Per il fotone non è invece necessaria alcuna modifica, perché se parte da A polarizzato nella direzione X, arriverà in B ancora polarizzato lungo la stessa direzione con ampiezza F(da A a B).

La polarizzazione produce un gran numero di accoppiamenti diversi. Ad esempio, c'è un'ampiezza perché un elettrone nello stato 2 assorba un fotone polarizzato lungo X e passi nello stato 3. Non vi è accoppiamento tra tutte le possibili combinazioni della polarizzazione di elettroni e fotoni, ma quelle che si accoppiano lo fanno con ampiezza j, talvolta con un'ulteriore rotazione della freccia di un multiplo di 90°.

I diversi tipi di polarizzazione possibili e i relativi valori dell'accoppiamento possono essere ottenuti in maniera molto bella ed elegante dai princìpi dell'elettrodinamica quantistica più le seguenti due ipotesi addizionali: 1) il risultato di un esperimento non cambia se l'apparato viene complessivamente ruotato in una direzione differente; 2) analogamente, non fa alcuna differenza se l'apparato si trova su un'astronave in moto con velocità arbitraria uniforme (questo non è altro che il principio di relatività).

Questa elegante analisi generale mostra che ogni particella deve appartenere a una classe di polarizzazione. Le varie classi si comportano in modo differente e vengono chiamate spin 0, spin 1/2, spin 1, spin 3/2, spin 2 e così via. Il comportamento più semplice è quello delle particelle di spin 0 che hanno una sola componente, cioè non hanno alcuna polarizzazione. (Gli elettroni e i fotoni fittizi considerati in queste lezioni sono stati trattati come particelle di spin 0. Tuttavia finora non è stata trovata alcuna particella fondamentale di spin 0). L'elettrone reale costituisce un esempio di particella di spin 1/2 e il fotone reale un esempio di particella di spin 1. Le particelle di spin 1/2 e 1 hanno quattro componenti. Gli altri tipi ne avrebbero di più, ad esempio le particelle di spin 2 avrebbero 10 componenti.

La connessione tra relatività e polarizzazione è semplice ed elegante, come ho detto, qualità che certo non riuscirei a raggiungere nella mia spiegazione e che richiederebbe da sola un'altra conferenza. I dettagli legati alla polarizzazione, pur non essendo essenziali per cogliere lo spirito e la fisionomia dell'elettrodinamica quantistica, lo sono per il calcolo corretto di ogni processo reale e spesso hanno effetti rilevanti.

In queste lezioni ho parlato soprattutto di interazioni tra elettroni e fotoni a distanze molto piccole e in condizioni relativamente semplici, in cui intervengono solo poche particelle. Ma vorrei aggiungere qualche considerazione su come appaiono tali interazioni nel mondo macroscopico, dove avviene lo scambio di un numero estremamente elevato di fotoni. In queste situazioni il calcolo delle frecce diventa molto complicato.

Alcune situazioni non sono però particolarmente complesse da analizzare. Ad esempio, in alcuni casi l'ampiezza per l'emissione di un fotone da parte di una sorgente è indipendente dalla precedente emissione di altri fotoni. Ciò si verifica quando la sorgente è molto pesante (un nucleo atomico), o quando vi sono moltissimi elettroni che si muovono tutti nello stesso modo, come avviene nella corrente che va avanti e indietro nell'antenna di una stazione trasmittente o che circola nell'avvolgimento di un elettromagnete. In questi casi viene emesso un gran numero di fotoni, tutti dello stesso tipo. In tali condizioni l'ampiezza per l'assorbimento di un fotone da parte di un elettrone risulta indipendente dal fatto che vi sia stato o no assorbimento di altri fotoni da parte dello stesso o di altri elettroni. Perciò il comportamento dell'elettrone è completamente descritto dall'ampiezza per l'assorbimento di un fotone, che dipende solo dalla posizione spaziotemporale dell'elettrone. (Una situazione di questo genere viene descritta dai fisici usando parole comuni. Essi dicono che l'elettrone si muove in un campo esterno. La parola «campo» viene usata in fisica per descrivere grandezze il cui valore dipende dalla posizione spaziale e temporale. Un buon esempio è dato dalla temperatura dell'aria, che dipende da dove e da quando viene misurata). Se si tiene conto della polarizzazione, il campo può avere più componenti. (Così il campo della luce ha quattro componenti, corrispondenti alle ampiezze per assorbire un fotone con polarizzazione X, Y, Z o T, che in linguaggio tecnico sono chiamate potenziali, vettore e scalare. In fisica classica, a partire da questi potenziali, si introducono altre grandezze, di uso più comodo, chiamate campi elettrico e magnetico).

In presenza di campi elettrici e magnetici variabili lentamente nel tempo, l'ampiezza relativa alla propagazione di un elettrone tra due punti molto distanti dipende dal percorso seguito. Come si è già visto nel caso della luce, la traiettoria più importante risulta quella per la quale le ampiezze relative ai percorsi vicini hanno tutte quasi la stessa direzione. Di conseguenza la particella non viaggia necessariamente in linea retta.

Questo ci riporta alla fisica classica, secondo la quale l'elettrone si muove attraverso campi di forza seguendo il percorso che rende minima una certa quantità. (I fisici chiamano «azione» tale quantità ed esprimono questa legge col nome di «principio di minima azione»). Questo è un esempio di come le leggi dell'elettrodinamica quantistica descrivono i fenomeni su scala macroscopica. Da qui si potrebbe andare in moltissime direzioni, che purtroppo non avremo tempo di esplorare in questa sede. Ho voluto solo ricordare che i fenomeni osservati nel mondo macroscopico e i bizzarri effetti che avvengono su scala microscopica sono entrambi prodotti dalla interazione di fotoni ed elettroni e, in ultima analisi, sono tutti descritti dalla teoria dell'elettrodinamica quantistica.