II
I FOTONI: PARTICELLE DI LUCE

Questa è la seconda di una serie di conferenze sull'elettrodinamica quantistica, e poiché vedo che il pubblico è completamente diverso (evidentemente perché ho detto che non si sarebbe capito nulla), riassumerò in breve il contenuto della prima lezione.

Abbiamo parlato della luce. La prima caratteristica importante della luce è che si comporta come se fosse formata da particelle: quando una luce monocromatica (cioè di un solo colore) molto debole colpisce un rivelatore, questo emette un ticchettio che diventa meno frequente, ma conserva la stessa intensità, via via che la luce viene resa più fioca.

L'altro aspetto importante del comportamento della luce riguarda la riflessione parziale della luce monocromatica. In media viene riflesso il 4% dei fotoni che colpiscono una singola superficie di vetro. Questo è già un mistero, poiché risulta impossibile prevedere quali fotoni rimbalzeranno e quali passeranno. Se poi si inserisce una seconda superficie, i risultati sono decisamente strani: invece della riflessione dell'8% che ci si aspetterebbe dalle due superfici, la riflessione parziale può essere amplificata fino al 16% o eliminata del tutto, a seconda dello spessore del vetro.

Questo strano aspetto della riflessione parziale da due superfici può essere spiegato dalla teoria ondulatoria finché si considera luce abbastanza intensa, ma tale teoria non può spiegare come mai il rivelatore continui a ticchettare con la stessa intensità allorché la luce diventa molto fioca. L'elettrodinamica quantistica «risolve» questa dualità ondulatorio-corpuscolare asserendo che la luce è formata da particelle (come sosteneva Newton). Tuttavia questo enorme progresso della scienza ha avuto come prezzo una «ritirata» della fisica, che ora è in grado di calcolare solo la probabilità che un dato fotone colpisca il rivelatore, senza offrire un buon modello intuitivo di come ciò avvenga effettivamente.

Nella prima lezione ho descritto come fanno i fisici a calcolare la probabilità che un determinato evento si verifichi. Si disegnano delle frecce su un foglio di carta secondo le seguenti regole.

 

PRINCIPIO FONDAMENTALE: la probabilità che un evento si verifichi è data dal quadrato della lunghezza di una freccia detta «ampiezza di probabilità». Ad esempio, una freccia lunga 0,4 rappresenta una probabilità di 0,16, cioè del 16%.

 

REGOLA GENERALE per disegnare la freccia relativa a un evento che può prodursi in più modi alternativi: si tracci una freccia per ciascun modo, e poi si combinino le varie frecce (le si «sommi») unendo la coda di ciascuna alla punta della precedente. Si disegni infine una «freccia risultante», unendo la coda della prima freccia alla punta dell'ultima. Il quadrato di questa freccia finale dà la probabilità complessiva che l'evento considerato si verifichi.

 

Ho poi illustrato le regole specifiche per disegnare le frecce nel caso della riflessione parziale sul vetro (si veda il capitolo precedente alle pp. 42-44 [intorno alle figure 8-11 in questo eBook]).

Questo per quanto riguarda il contenuto della prima lezione.

Ora vi farò vedere come questo modello del mondo, così radicalmente diverso da ogni descrizione a voi nota (e appunto per questo, magari, preferireste non saperne più niente), è in grado di spiegare tutte le proprietà più conosciute della luce: ad esempio, perché la luce viene riflessa da uno specchio con un angolo di riflessione uguale a quello di incidenza; perché si piega passando dall'aria all'acqua; perché in un mezzo omogeneo si propaga in linea retta; perché viene focalizzata dalle lenti e così via. La teoria descrive correttamente anche proprietà meno conosciute. In effetti, la difficoltà maggiore che ho incontrato nel preparare queste lezioni è stata di resistere alla tentazione di discutere tutte le proprietà della luce che di solito vengono faticosamente studiate a scuola, come il comportamento della luce quando penetra nella zona d'ombra al di là di uno spigolo netto (fenomeno noto come diffrazione). Ma poiché la maggior parte di voi non avrà mai fatto molta attenzione a tali fenomeni, li lascerò perdere. Vi garantisco però (altrimenti gli esempi che sto per fare sarebbero fuorvianti) che tutti i fenomeni osservati in cui interviene la luce possono essere spiegati dall'elettrodinamica quantistica; io qui mi limiterò a quelli più semplici e più comuni.

Fig. 19. Secondo la fisica classica, uno specchio riflette la luce solo nel punto in cui l'angolo di riflessione è uguale a quello di incidenza, anche quando sorgente e rivelatore sono a distanze diverse dallo specchio, come nel caso (b).

Comincerò dal problema di determinare come la luce si riflette su uno specchio (fig. 19). In S è situata una sorgente che emette luce monocromatica (mettiamo ancora rossa) di bassissima intensità: un fotone alla volta. In P si trova un fotomoltiplicatore che rivela i fotoni, e poiché è più facile tracciare le frecce se la configurazione è simmetrica, poniamolo, rispetto allo specchio, alla stessa distanza della sorgente. Si vuole calcolare la probabilità che il rivelatore faccia un «clic» in seguito all'emissione di un fotone dalla sorgente. Poiché c'è anche la possibilità che un fotone vada direttamente nel rivelatore, interponiamo uno schermo in Q.

Ci aspetteremmo che tutta la luce che arriva al rivelatore sia stata riflessa dalla parte centrale dello specchio, perché solo in tale zona l'angolo di incidenza è uguale a quello di riflessione, mentre le parti dello specchio vicine alle estremità dovrebbero essere completamente estranee a tutta la faccenda. Giusto?

Così parrebbe, ma vediamo che cosa dice la teoria quantistica. Principio fondamentale: la probabilità che un evento si verifichi è data dal quadrato della freccia risultante ottenuta tracciando una freccia per ciascun modo in cui l'evento può avvenire e poi combinando («sommando») le varie frecce. Nell'esperimento in cui si considerava la riflessione parziale della luce da due superfici, un fotone poteva arrivare dalla sorgente al rivelatore in due modi. Nell'esperimento che stiamo discutendo ora ci sono invece milioni di percorsi che un fotone può seguire: può andare a colpire l'estremità sinistra dello specchio, ad esempio in A o in B, e di lì rimbalzare fino al rivelatore (fig. 20); può rimbalzare nel punto che voi vi aspettereste, cioè al centro, in G; oppure andare fino all'estremità destra dello specchio, in K o in M, e di lì al rivelatore. Forse penserete che sono diventato matto, perché per la maggior parte di questi percorsi gli angoli di incidenza e di riflessione non sono uguali. Nossignori, non sono matto: la luce si propaga proprio così! Ma come può essere?

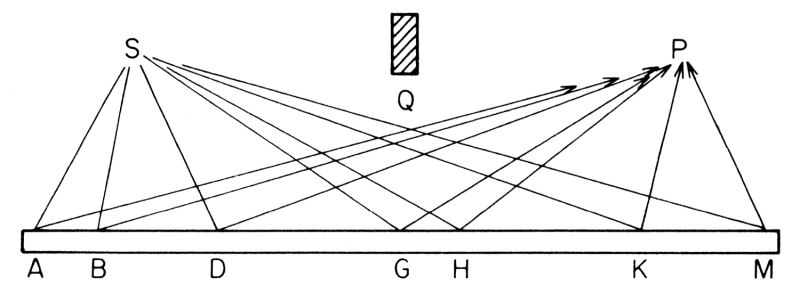
Fig. 20. Secondo l'elettrodinamica quantistica, la luce ha la stessa ampiezza di probabilità di riflettersi in ogni punto dello specchio, da A a M.

Per facilitare le cose, supponiamo che lo specchio sia costituito semplicemente da un lunga striscia che va da sinistra a destra, dimenticando per un momento che esso si estende anche fuori dal piano della carta (fig. 21). Inoltre, mentre la luce può riflettersi in un numero immenso di punti, facciamo per ora l'approssimazione di suddividere lo specchio in un numero finito di piccoli quadrati e di considerare un solo percorso per ciascun quadrato; più piccoli sono i quadrati, e più numerosi quindi sono i percorsi presi in considerazione, più il calcolo diventa accurato, ma anche complicato.

Fig. 21. Per calcolare più facilmente come si propaga la luce, si consideri momentaneamente solo una striscia di specchio divisa in tanti piccoli quadrati e un solo percorso per ciascun quadrato. Questa semplificazione non pregiudica in alcun modo l'accuratezza dell'analisi.

Per ogni possibile percorso della luce si disegni ora una piccola freccia, che avrà una certa lunghezza e una certa direzione. Cominciamo con la lunghezza. Si potrebbe pensare che la freccia corrispondente al percorso che passa per il punto centrale dello specchio, G, sia decisamente la più lunga, poiché sembra esservi un'elevatissima probabilità che un fotone che arriva nel rivelatore abbia seguito tale cammino, mentre le frecce relative a cammini che passano per le estremità dello specchio dovrebbero essere molto piccole. E invece no: tale regola sarebbe completamente arbitraria. La regola corretta, che descrive ciò che realmente accade, è molto più semplice: la probabilità che ha un fotone di giungere nel rivelatore è quasi la stessa qualunque sia il percorso seguito, per cui le nostre frecce hanno tutte quasi la stessa lunghezza. (Vi sono, a dire il vero, alcune piccole differenze dovute alla diversità di angolo e di distanza, ma sono talmente secondarie che le trascurerò). Tutte le frecce avranno dunque la stessa lunghezza arbitraria: scegliamola molto piccola perché le frecce sono molte, corrispondenti a moltissimi percorsi possibili (fig. 22).

Fig. 22. Nei calcoli che verranno discussi, ogni percorso che la luce può seguire sarà rappresentato da una freccia di lunghezza arbitraria fissata, come in figura.

Mentre si può tranquillamente assumere che la lunghezza di tutte le frecce sia più o meno la stessa, le loro direzioni sono chiaramente diverse, essendo diverso il tempo impiegato a seguire i vari percorsi; si ricordi che, come ho spiegato nella prima lezione, la direzione di una data freccia è determinata dalla posizione di arrivo di un'immaginaria lancetta di cronometro, che ruota mentre il fotone segue il suo percorso. Un fotone che vada prima all'estremità sinistra dello specchio, in A, impiega chiaramente più tempo per arrivare nel rivelatore di un altro fotone che si rifletta nella zona centrale dello specchio, in G (fig. 23).

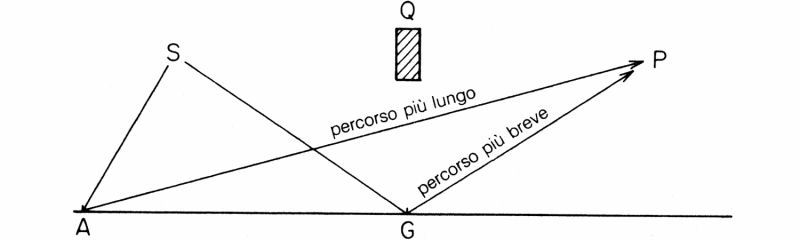
Fig. 23. Mentre la lunghezza delle varie frecce è essenzialmente la stessa, la loro direzione è diversa perché sono diversi i tempi impiegati da un fotone per seguire percorsi diversi. È evidente che occorre più tempo per andare da S in A e poi in P che non da S in G e poi in P.

Immaginate di avere fretta e di dover correre dalla sorgente allo specchio e poi di lì al rivelatore: capireste subito che non è il caso di andare prima fino in A e poi risalire fino al rivelatore; si fa molto prima a toccare lo specchio in un punto della zona centrale.

Per facilitare il calcolo della direzione delle varie frecce, disegnerò un grafico sotto la raffigurazione schematica dello specchio (fig. 24).

Fig. 24. Nella parte superiore della figura sono mostrati i percorsi che la luce può seguire (nella nostra situazione semplificata), mentre i punti corrispondenti nel grafico sottostante indicano il tempo che un fotone impiega per andare dalla sorgente a quel punto e di lì al fotomoltiplicatore. Subito sotto il grafico sono rappresentate le direzioni delle varie frecce e, sotto ancora, il risultato della loro somma. È evidente che il contributo principale alla lunghezza della freccia finale proviene dalle frecce comprese tra È ed I, le cui direzioni sono quasi le stesse, perché i tempi relativi ai corrispondenti percorsi sono quasi gli stessi. Questa è anche la zona in cui il tempo impiegato è minimo. E perciò approssimativamente corretto dire che la luce segue il percorso che richiede il minimo tempo.

In corrispondenza di ciascun punto dello specchio è indicato, lungo la verticale, il tempo impiegato dalla luce per giungere nel rivelatore seguendo il percorso che passa per quel punto. Quanto maggiore è questo tempo, tanto più in alto nel grafico sarà il punto corrispondente. Incominciamo da sinistra: un fotone che si riflette in A impiegherà un tempo piuttosto lungo, cosicché il punto corrispondente nel grafico sarà piuttosto in alto. Spostandosi verso il centro dello specchio, il tempo impiegato diminuisce, e i punti sul grafico sono via via più in basso. Superato il centro, il tempo necessario a seguire un percorso ricomincia a crescere, e il punto corrispondente nel grafico verrà a trovarsi sempre più in alto. Per aiutare l'occhio, congiungiamo i vari punti: otterremo una curva simmetrica che inizia dall'alto, scende e poi risale.

Che cosa significa ciò per la direzione delle nostre frecce? La direzione di ciascuna di esse è in corrispondenza col tempo impiegato da un fotone a percorrere un determinato percorso. Disegniamo le varie frecce cominciando da sinistra. Il percorso A richiede il tempo maggiore e la freccia corrispondente sarà orientata in una certa direzione. La freccia per il percorso B sarà orientata lungo una direzione diversa perché il tempo impiegato è diverso. Le frecce relative ai percorsi F, G ed H, che passano per la zona centrale dello specchio, avranno invece direzione pressoché identica perché i tempi corrispondenti sono quasi gli stessi. Superato il centro dello specchio, si vede che ad ogni percorso sul lato destro dello specchio corrisponde un percorso sul lato sinistro che ha lo stesso tempo di percorrenza (questa è una conseguenza della decisione di porre sorgente e rivelatore alla stessa distanza dallo specchio e simmetrici rispetto al suo centro). La freccia per il percorso J, ad esempio, avrà la stessa direzione di quella per il percorso D.

Adesso sommiamo le varie frecce, partendo dalla freccia A e agganciando la coda di ciascuna alla punta della precedente. Se volessimo fare una passeggiata usando le frecce come passi, all'inizio non ci allontaneremmo gran che dal punto di partenza, perché ogni passo porta in una direzione molto diversa dal precedente. Dopo un po', però, le frecce cominciano a rivolgersi tutte pressappoco nella stessa direzione, e allora si progredisce decisamente. Verso la fine della passeggiata ciascun passo è di nuovo in una direzione del tutto diversa dal precedente, per cui non si avanza più.

Non resta che tracciare la freccia risultante. Si congiunge la coda della prima freccia alla punta dell'ultima e si ottiene lo spostamento complessivo della passeggiata. E notate bene che la freccia finale ha lunghezza non trascurabile! L'elettrodinamica quantistica predice che la luce effettivamente si riflette su uno specchio!

Questo risultato richiede alcune considerazioni. Che cosa determina la lunghezza della freccia finale? Vediamo anzitutto che le estremità dello specchio non hanno nessuna importanza: le frecce relative a questi contributi puntano in tutte le direzioni, ma non producono alcuno spostamento complessivo. Se si tagliassero queste estremità, che a voi saranno subito apparse, istintivamente, di nessunissimo interesse, la lunghezza della freccia finale non risulterebbe quasi per niente modificata.

Quale parte dello specchio dà dunque a tale freccia la sua lunghezza apprezzabile? Chiaramente quella le cui frecce hanno tutte quasi la stessa direzione, perché il tempo corrispondente è quasi lo stesso. Osservando il grafico in cui sono riportati i tempi relativi ai vari percorsi (fig. 24), si vede che le variazioni da un percorso al successivo sono molto ridotte nella zona più bassa della curva, dove il tempo impiegato è minimo.

Riassumendo, la zona per cui il tempo è minimo è anche quella per cui tempi relativi a percorsi vicini sono quasi gli stessi; le frecce relative a questa zona sono orientate tutte pressappoco nella stessa direzione e si sommano dando un contributo apprezzabile; questa è la zona che determina la probabilità con cui un fotone si riflette su uno specchio. Ed è per questo che, approssimando, possiamo prendere per buona la descrizione del mondo, piuttosto rozza, secondo la quale la luce segue soltanto il percorso che richiede il minimo tempo. (È facile dimostrare che per tale percorso l'angolo d'incidenza è uguale all'angolo di riflessione, ma per brevità non lo faremo).

L'elettrodinamica quantistica fornisce dunque la risposta corretta: la zona centrale dello specchio è quella rilevante nel determinare la riflessione; ma questa risposta è stata ottenuta al prezzo di dover credere che la luce si riflette in tutti i punti dello specchio e di dover sommare un gran numero di piccole frecce il cui solo effetto è di cancellarsi tra loro. Tutto ciò può sembrare una perdita di tempo, un giochino stupido buono solo per i matematici. Non sembra «fisica vera» dover introdurre qualcosa solo per poi cancellarlo.

Per verificare se davvero c'è riflessione in tutti i punti dello specchio, facciamo un altro esperimento. Cominciamo con l'eliminare gran parte dello specchio, lasciandone circa un quarto, all'estremità sinistra. 11 pezzo rimasto è ancora abbastanza grande, ma è nel posto sbagliato. Si è appena visto (fig. 24) che le frecce relative ai contributi dell'estremità sinistra dello specchio hanno direzioni molto diverse tra loro a causa della notevole differenza di tempo tra percorsi adiacenti. Facciamo adesso un calcolo più accurato, suddividendo la parte rimasta dello specchio in intervalli molto più piccoli, tali che non ci sia molta differenza di tempo tra percorsi vicini (fig. 25).

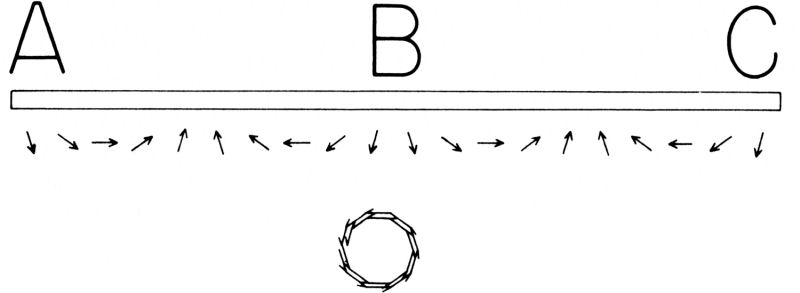
Fig. 25. Per verificare che la riflessione ha luogo effettivamente anche alle estremità dello specchio (anche se poi si elide nella somma finale), si può fare un esperimento con un grande pezzo di specchio disposto in posizione errata per dar luogo alla riflessione da S a P. Si consideri questo pezzo di specchio suddiviso in tratti molto più piccoli, così che il tempo impiegato differisca di poco da un percorso al successivo. Quando tutte le frecce vengono sommate il risultato è nullo: le varie frecce sono disposte in cerchio e la loro somma è praticamente zero.

In questa rappresentazione più dettagliata vediamo che alcune frecce puntano più o meno verso destra mentre le altre puntano più o meno verso sinistra. Quando si sommano tutte le frecce si vede che esse sono disposte sostanzialmente lungo una circonferenza, e che quindi non si arriva da nessuna parte. Ma supponiamo di raschiar via per bene dallo specchio le zone a cui corrispondono frecce dirette prevalentemente in una data direzione, ad esempio verso sinistra, in modo che rimangano solo le zone le cui frecce puntano prevalentemente nella direzione opposta (fig. 26).

La somma delle frecce dirette tutte più o meno verso destra darà una serie di semicerchi e produrrà una freccia risultante apprezzabile; in base alla teoria adesso si dovrebbe osservare una riflessione notevole! E infatti così è: la teoria è corretta! Uno specchio del genere viene chiamato reticolo di diffrazione e funziona a meraviglia.

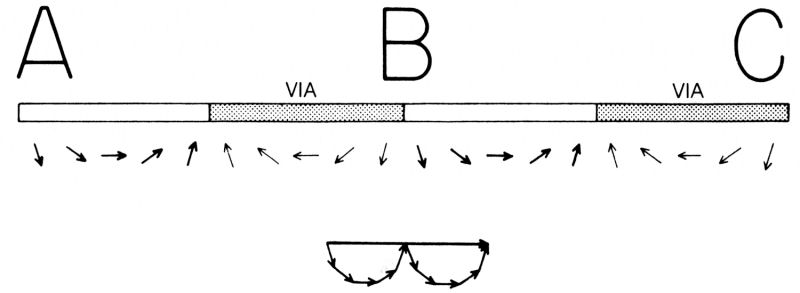
Fig. 26. Se si sommano solo le frecce inclinate verso una particolare direzione, ad esempio verso destra, e si eliminano le altre raschiando il vetro nei punti corrispondenti, si osserva che una notevole quantità di luce viene riflessa dal pezzo di specchio situato nel posto sbagliato. Uno specchio opportunamente raschiato è chiamato reticolo di diffrazione.

Non è fantastico? Si prende un pezzo di specchio su cui non ci si aspetterebbe alcuna riflessione, se ne raschia via una parte ed ecco che lo specchio riflette!⁶

Questo particolare reticolo è fatto su misura per la luce rossa, e non funzionerebbe con luce blu, per la quale occorre invece un reticolo in cui i tratti eliminati siano più vicini tra loro, perché, come ho detto nella prima lezione, la lancetta del cronometro immaginario deve girare più velocemente quando segue un fotone blu che quando ne segue uno rosso. Le strisce opache adatte per la velocità di rotazione del rosso non si trovano nei posti giusti per il blu; le frecce si ingarbugliano e il reticolo non funziona bene. Il caso vuole però che se si sposta il rivelatore in modo che formi un angolo leggermente diverso, il reticolo adatto alla luce rossa diventa adatto a quella blu. Si tratta solamente di un caso fortunato, dovuto alla particolare configurazione geometrica del sistema (fig. 27).

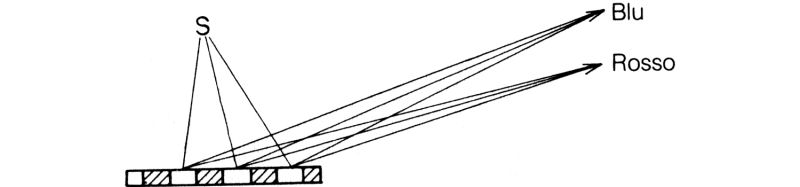
Fig. 27. Un reticolo di diffrazione i cui solchi sono distanziati correttamente per la luce rossa funziona anche per gli altri colori se si pone il rivelatore in posizione differente. Pertanto, a seconda dell'angolo di osservazione, è possibile vedere diversi colori riflessi da una superficie rigata, ad esempio quella di un disco di grammofono.

Illuminando il reticolo con luce bianca, il rosso emergerà ad un certo angolo, l'arancione a un angolo leggermente maggiore, poi verranno il giallo, il verde e il blu, e tutti i colori dell'arcobaleno. Succede comunemente di vedere riflessa luce di vari colori quando si guarda sotto l'angolo giusto un oggetto, illuminato con luce bianca, su cui è incisa una serie di solchi sufficientemente vicini tra loro, ad esempio un disco di grammofono o ancor meglio un videodisco. Avrete certo visto quei meravigliosi adesivi argentati che qui, nell'assolata California, vengono spesso incollati sul retro delle automobili: quando l'automobile si muove si vedono vivaci colori cangianti dal rosso al blu. Adesso sapete da dove vengono: a causarli è un reticolo di diffrazione, uno specchio raschiato nei punti giusti. Il sole è la sorgente di luce e gli occhi sono i rivelatori. A questo punto potrei spiegare in termini facili come funzionano i laser e gli ologrammi, ma so che non tutti ne hanno conoscenza diretta, e poi ci sono molte altre cose di cui voglio parlare.⁷

Fig. 28. La Natura ha prodotto molti tipi di reticoli di diffrazione sotto forma di cristalli. Un cristallo di sale riflette solo per alcuni angoli i raggi X, che sono luce per la quale la lancetta del cronometro immaginario ruota a grandissima velocità, anche 10.000 volte maggiore che per la luce visibile. Dagli angoli di riflessione si può risalire all'esatta disposizione spaziale dei singoli atomi.

Un reticolo di diffrazione dimostra quindi che non si possono trascurare le parti di uno specchio che non sembrano contribuire alla riflessione; manipolandolo opportunamente si può mettere in evidenza la realtà della riflessione da tutti i suoi punti e produrre, alcuni fenomeni ottici sorprendenti.

Ma ancor più importante è il fatto che, dimostrando la realtà del contributo di tutte le parti dello specchio alla riflessione, si dimostra che c'è un'ampiezza (una freccia) per ciascun modo in cui un evento può accadere. E per calcolare correttamente la probabilità di un tale evento nelle diverse circostanze, occorre sommare le frecce relative a tutti i modi in cui esso può verificarsi, e non solo a quelli che si ritengono rilevanti!

Parlerò adesso di un fenomeno più familiare dei reticoli di diffrazione, cioè del passaggio della luce dall'aria all'acqua. Immaginiamo che un fotomoltiplicatore possa essere immerso nell'acqua, e collochiamolo nella posizione D, mentre la sorgente si trova nell'aria, in S (fig. 29).

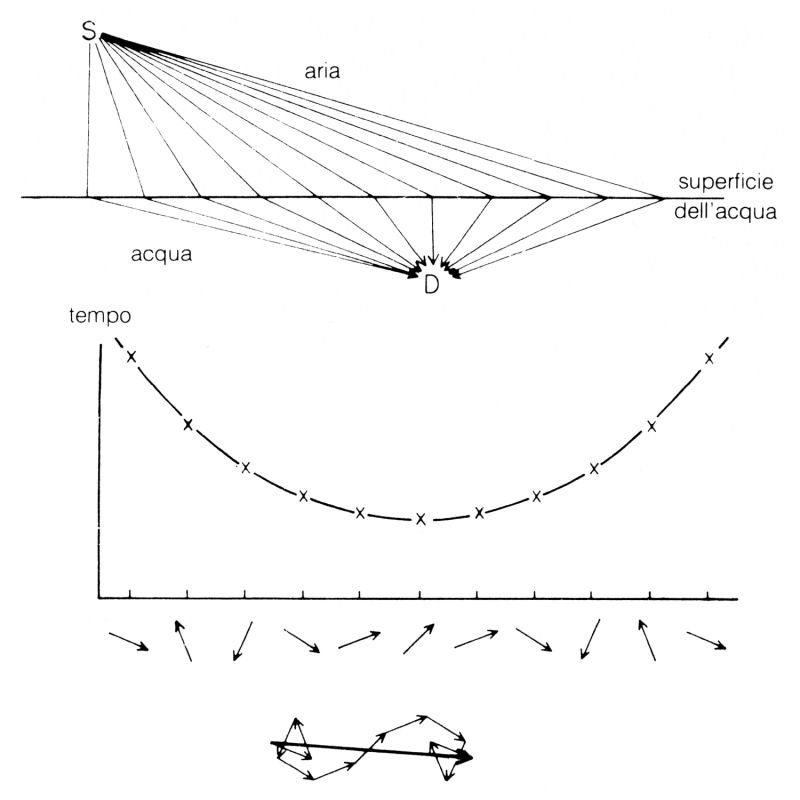
Fig. 29. Secondo la teoria quantistica, la luce può andare da una sorgente nell'aria a un rivelatore nell'acqua seguendo molti percorsi. Se si semplifica il problema, come nel caso dello specchio, si può riportare in un grafico il tempo relativo ai valori percorsi, e sotto di esso tracciare la direzione delle relative frecce. Anche questa volta i contributi maggiori alla lunghezza della freccia risultante vengono da quei percorsi le cui frecce puntano pressappoco nella stessa direzione, perché i tempi corrispondenti sono quasi gli stessi, e anche questa volta ciò avviene quando il tempo impiegato è minimo.

Anche in questo caso vogliamo calcolare la probabilità che un fotone arrivi dalla sorgente al rivelatore. Per farlo dobbiamo prendere in considerazione tutti i possibili percorsi della luce. Ciascuno di questi percorsi aggiunge una piccola freccia e, come nell'esempio precedente, tutte queste frecce hanno quasi la stessa lunghezza. Se facciamo un grafico del tempo necessario a un fotone per compiere ciascuno dei possibili percorsi, la curva che si ottiene è molto simile a quella che si aveva per la luce riflessa da uno specchio: parte dall'alto, scende e poi sale di nuovo; il contributo più importante viene dai luoghi per i quali le frecce puntano pressappoco nella stessa direzione, cioè per i quali il tempo di percorrenza varia poco tra percorsi vicini, ossia dalla parte più bassa della curva. Questa è anche la zona per cui il tempo è minimo, sicché in realtà basta trovare il percorso di minimo tempo.

Ora, la luce sembra propagarsi più lentamente nell'acqua che nell'aria (il perché lo spiegherò nella prossima lezione), e ciò rende il percorso attraverso l'acqua più ‘dispendioso’, per così dire, di quello attraverso l'aria. Non è difficile individuare quale percorso richieda il minimo tempo: immaginate di essere un bagnino seduto in S, e che in D ci sia una bella ragazza che sta per affogare (fig. 30). Poiché correre sulla terra è più veloce che nuotare, in che punto entrereste in acqua per raggiungere la bagnante che annega nel più breve tempo possibile?

Fig. 30. Trovare il percorso di minimo tempo per la luce è come trovare il percorso che richiede meno tempo a un bagnino che deve attraversare di corsa una spiaggia e poi nuotare per salvare una persona che affoga: lungo il percorso più corto c'è troppa acqua, mentre lungo quello con meno acqua c'è troppa spiaggia; il percorso che richiede il minimo tempo è un compromesso tra i due.

Entrereste in acqua al punto A, per poi mettervi a nuotare come forsennati? Naturalmente no. Ma anche correre direttamente verso la ragazza in pericolo, entrando nell'acqua in J, non è il percorso più rapido. È chiaro che un bagnino non si ferma a fare simili analisi in circostanze d'emergenza, ma è possibile calcolare quale percorso richiede il minimo tempo: si tratta di un compromesso tra il percorso diritto, che passa per J, e quello con meno acqua, che passa per N. La stessa cosa succede per la luce: il percorso che richiede il minimo tempo entra nell'acqua in un punto tra J ed N, ad esempio in L.

Un altro fenomeno cui voglio accennare brevemente è quello del miraggio. Guidando su una strada molto calda, si ha a volte l'impressione di vederla piena di pozzanghere. In realtà quello che si vede è il riflesso del cielo; però quando si vede il cielo sulla strada è perché ci sono delle pozzanghere (riflessione parziale su una singola superficie!). Come mai allora si vede il cielo riflesso sulla strada quando non c'è la minima traccia d'acqua? Bisogna sapere che la luce viaggia più lentamente attraverso l'aria fredda che attraverso quella calda, e per poter vedere il miraggio, l'osservatore deve trovarsi nella zona d'aria più fredda che è sopra lo strato d'aria calda immediatamente vicino alla superficie della strada (fig. 31).

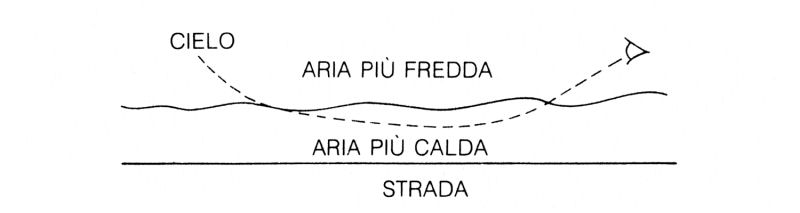
Fig. 31. Trovare il percorso di minimo tempo spiega anche come si produce un miraggio. La luce viaggia più velocemente nell'aria calda che in quella fredda. Quando si vede il riflesso del cielo sulla strada è perché parte della luce del cielo che arriva nell'occhio proviene dalla strada. Poiché l'unica altra situazione in cui si vede il cielo sulla strada si verifica quando c'è acqua che lo riflette, il miraggio viene attribuito alla presenza di acqua.

Come sia possibile vedere il cielo guardando in giù può essere compreso trovando il percorso di minimo tempo. Provate a pensarci da soli: è un problema divertente e abbastanza facile.

Negli esempi finora discussi (riflessione della luce su uno specchio o il suo passaggio dall'aria all'acqua) ho fatto un'approssimazione: per semplicità ho disegnato i percorsi seguiti dalla luce come due tratti rettilinei che formano un angolo tra loro. Ma non c'è bisogno di assumere che la luce si propaghi in linea retta quando viaggia attraverso un materiale omogeneo come l'acqua o l'aria; anche questo può essere spiegato in base al principio generale della teoria quantistica: la probabilità di un evento si trova sommando le frecce relative a tutti i modi in cui quell'evento può accadere.

Perciò, sommando freccette, farò vedere nel prossimo esempio come si possa avere l'impressione che la luce si propaghi in linea retta. Disponiamo una sorgente e un rivelatore rispettivamente in S e in P (fig. 32) e consideriamo tutti i percorsi, comunque contorti, che la luce può seguire per andare dalla sorgente al fotomoltiplicatore. Disegniamo la freccetta relativa a ciascun cammino, e vediamo se si è imparata la lezione!

Per ogni percorso contorto, ad esempio A, c'è un percorso vicino un po' più diritto e decisamente più breve, che cioè prende molto meno tempo. Ma se si considerano percorsi quasi rettilinei, come C, quelli vicini e leggermente più diritti richiedono quasi lo stesso tempo. Per questi ultimi percorsi le frecce si sommano invece di elidersi ed essi sembrano i soli seguiti dalla luce.

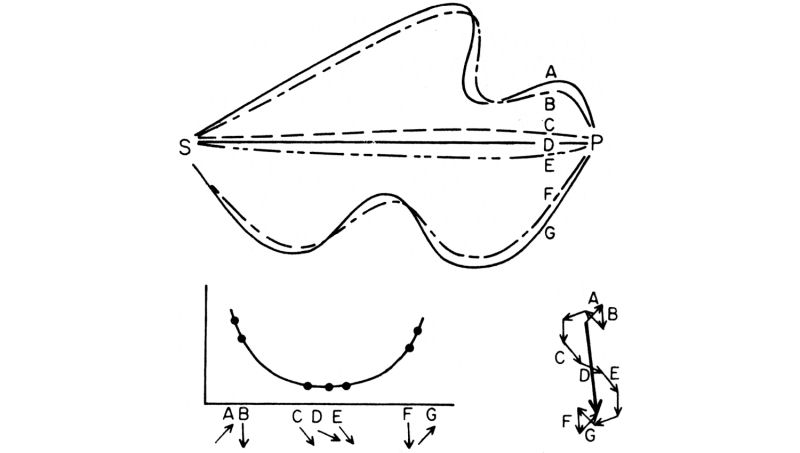
Fig. 32. Usando la teoria quantistica, si può capire perché la luce sembra viaggiare in linea retta. Se si prendono in considerazione tutti i percorsi possibili, si vede che per ogni percorso contorto ce n'è uno vicino di lunghezza notevolmente inferiore, che richiede perciò molto meno tempo e la cui freccia ha una direzione notevolmente diversa. Solo i percorsi vicini a quello rettilineo che passa per D hanno frecce che puntano tutte quasi nella stessa direzione, perché i tempi relativi sono quasi gli stessi. Soltanto tali frecce risultano importanti, perché sono le uniche a dar luogo a una freccia finale apprezzabile.

È importante osservare che la freccia relativa al solo percorso diritto, quello che passa per D, non è sufficiente a dar conto della probabilità con cui la luce arriva dalla sorgente al rivelatore. Anche i percorsi quasi diritti e vicini, attraverso C o E, per esempio, danno contributi importanti. Per cui la luce non viaggia realmente lungo una linea retta: essa ‘annusa’ i percorsi vicini e usa una piccola zona di spazio tutt'attorno. (Analogamente uno specchio deve avere dimensioni abbastanza grandi per dar luogo alla normale riflessione; se è troppo piccolo per poter riflettere tutto il fascio di percorsi importanti, diffonderà la luce in tutte le direzioni dovunque lo si metta).

Per esaminare meglio il comportamento di questo fascio di luce, mettiamo una sorgente in S, un fotomoltiplicatore in P e interponiamo tra loro due blocchi per evitare che i percorsi della luce si allontanino troppo da quello più breve (fig. 33).

Fig. 33. La luce non segue solo il percorso rettilineo, ma anche tutto il fascio dei percorsi vicini. Se due blocchi sono abbastanza separati da lasciar passare questo fascio, i fotoni vanno normalmente in P e quasi mai in Q.

Collochiamo anche un secondo fotomoltiplicatore in Q, sotto P, e assumiamo di nuovo, per semplicità, che la luce possa andare da S a Q solo seguendo percorsi fatti da due tratti rettilinei. Che cosa osserviamo? Se lo spazio tra i blocchi è sufficiente a permettere molti percorsi vicini, le frecce dei percorsi che arrivano in P si sommano, perché tali percorsi richiedono quasi lo stesso tempo, mentre quelle relative ai percorsi fino a Q si elidono, perché tra di essi vi sono sensibili differenze di tempo. Il fotomoltiplicatore in Q, perciò, non ticchetta.

Ma se avviciniamo i blocchi tra loro, a un certo punto il fotomoltiplicatore in Q inizia a ticchettare! Quando la fenditura tra i due blocchi tende a chiudersi, e vi sono perciò solo pochi percorsi vicini, anche le frecce dei percorsi in direzione di Q cominciano a sommarsi, perché tra loro non vi è quasi più differenza di tempo (fig. 34).

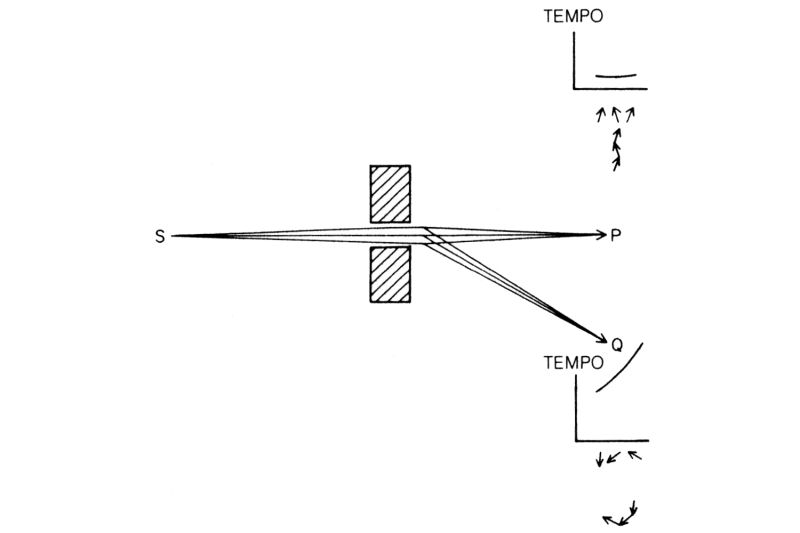
Fig. 34. Se si avvicinano i blocchi in modo che solo pochi percorsi diventino possibili, attraverso la stretta fenditura arriva in Q quasi altrettanta luce che in P, perché non ci sono abbastanza frecce che rappresentano i percorsi fino a Q per elidersi a vicenda.

Naturalmente tutt'e due le frecce risultanti saranno piccole, perché non passa molta luce, essendo la fenditura tanto stretta, ma il rivelatore in Q ticchetta quasi come quello in P! Ecco quindi che se si comprime troppo la luce, per essere sicuri che segua una linea retta, essa rifiuta di collaborare e comincia ad allargarsi.⁸

L'idea che la luce si propaghi in linea retta è dunque solo una comoda approssimazione per descrivere il suo comportamento in situazioni usuali, analoga a quella che si fa dicendo che, quando la luce si riflette su uno specchio, l'angolo di riflessione è uguale a quello di incidenza.

Ho mostrato prima un abile trucco con cui far vedere che la luce si riflette sotto molti angoli da uno specchio. Usando un sistema assai simile, possiamo costringere la luce ad andare da un punto a un altro seguendo parecchi percorsi.

Per semplificare, traccerò prima una linea tratteggiata verticale (fig. 35) tra la sorgente e il rivelatore (linea che non ha alcun significato, è solo artificiale!) e considererò soltanto i percorsi costituiti da due tratti rettilinei. Il tempo relativo a ciascun percorso lo riporto su un grafico simile a quello del caso dello specchio (solo che lo disegno rotato di 90 gradi): la linea dei tempi parte da A, all'estremità superiore, curva verso valori più piccoli, perché i percorsi nella zona centrale sono più corti e richiedono meno tempo, e infine si allontana nuovamente.

Fig. 35. L'analisi di tutti i possibili percorsi da S a P è più semplice se si considerano solo i percorsi fatti da due tratti rettilinei (in un solo piano). Il risultato è lo stesso che nel caso reale, più complicato: c'è sempre una curva dei tempi con un minimo, da cui proviene il contributo maggiore alla freccia finale.

Adesso divertiamoci un po' e proviamo a ‘imbrogliare la luce’, facendo in modo che tutti i percorsi richiedano lo stesso tempo. Ma come? Come si può ottenere che il percorso più corto, che passa per M, richieda lo stesso tempo del percorso più lungo che passa per A?

Si ricordi che la luce si muove più lentamente nell'acqua che nell'aria; altrettanto succede nel vetro (che però è molto più facile da lavorare!). Quindi, basterà inserire uno spessore adatto di vetro lungo il percorso più breve, che passa per M, e il tempo richiesto per tale percorso sarà esattamente uguale a quello necessario a passare per A. I percorsi vicini a M, che sono un pochino più lunghi, richiederanno un vetro un po' meno spesso (fig. 36).

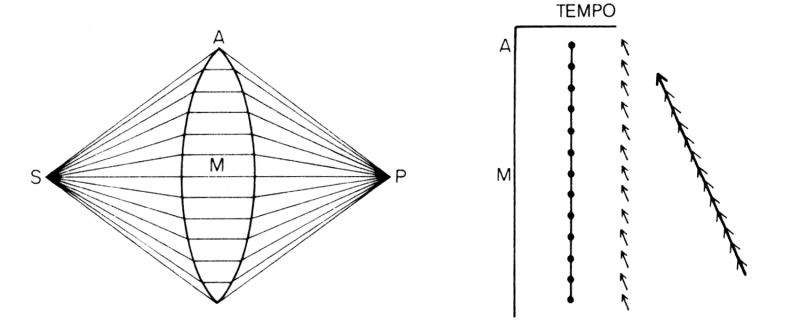
Fig. 36. Si può «imbrogliare» la Natura rallentando la luce che segue i percorsi più brevi: inserendo uno spessore adatto di vetro si fa in modo che tutti i percorsi richiedano lo stesso tempo. Allora tutte le frecce hanno la stessa direzione e si ottiene una freccia risultante favolosa — un'enorme quantità di luce! Un siffatto pezzo di vetro costruito in modo da aumentare la probabilità che la luce arrivi dalla sorgente a un dato punto viene detto lente convergente.

Più ci si avvicina ad A, meno vetro occorre inserire per rallentare la luce. Interponendo lungo ciascun percorso lo spessore di vetro appropriato a compensare il ritardo, si possono rendere uguali tra loro tutti i tempi di percorrenza. Disegnando le frecce per i vari possibili percorsi della luce, si trova adesso che si è riusciti ad allinearle tutte (e pensare che sono milioni!), per cui il risultato finale è spettacolare: una freccia risultante di lunghezza sorprendente! Naturalmente avrete capito che sto descrivendo una lente convergente. Sistemando le cose in modo che tutti i tempi siano uguali, si può focalizzare la luce, cioè sì può rendere molto elevata la probabilità che essa arrivi in un punto determinato e molto bassa la probabilità che arrivi in qualsiasi altro punto.

Questi esempi mostrano come l'elettrodinamica quantistica, che a prima vista sembra una teoria assurda, priva di causalità, senza un funzionamento chiaro, senza alcuna concretezza, riproduce fenomeni ben noti, quali la riflessione su uno specchio, la curvatura dei raggi luminosi nel passaggio dall'aria all'acqua, la focalizzazione delle lenti. Essa prevede anche altri fenomeni forse non altrettanto familiari, come il funzionamento del reticolo di diffrazione, e moltissimi altri. In breve, questa teoria descrive con successo qualunque fenomeno in cui interviene la luce.

Gli esempi discussi illustrano come calcolare la probabilità di un evento che può verificarsi in più modi alternativi tra loro: si disegna una freccia per ciascun modo e si sommano le frecce. «Sommare le frecce» vuol dire sovrapporre una coda alla punta precedente e tracciare poi la «freccia risultante». Il quadrato di questa freccia finale rappresenta la probabilità dell'evento.

Per farvi sentire meglio il «gusto» quantistico di questa teoria, vi farò vedere ora come i fisici calcolano la probabilità di un evento composto, cioè di un evento che può essere diviso in una serie di passi o che consiste di vari fatti che accadono indipendentemente.

Un esempio di evento composto lo si ottiene modificando il primo esperimento discusso, in cui alcuni fotoni rossi venivano inviati su una superficie di vetro per misurare la riflessione parziale. Al posto del fotomoltiplicatore (fig. 37) mettiamo uno schermo con un foro che lasci passare i fotoni che giungono in A. Mettiamo poi uno strato di vetro in B e piazziamo il fotomoltiplicatore in C. Come si calcola la probabilità che un fotone partito dalla sorgente arrivi in C?

Fig. 37. Un evento composto può essere analizzato come una successione di passi. In questo esempio il percorso seguito da un fotone per andare da S a C può venire diviso in due passi: 1) il fotone va da S ad A; 2) il fotone va da A a C. Ogni passo, analizzato separatamente, dà luogo a una freccia che può essere considerata da un punto di vista nuovo: come una freccia unitaria (cioè di lunghezza I e che segna le 12) che ha subito una contrazione e una rotazione. In questo esempio il passo 1 comporta una contrazione a 0,2 e una rotazione fino alle 2; il passo 2 una contrazione a 0,3 e una rotazione fino alle 5. L'ampiezza per due passi consecutivi si ottiene contraendo e ruotando in successione: la freccia unitaria iniziale viene ridotta e ruotata in modo da ottenere una freccia di lunghezza 0,2 che segna le 2, la quale viene a sua volta ridotta a 0,3 e ruotata dalle 12 alle 5, come se fosse la freccia unitaria; si ottiene così una freccia di lunghezza 0,06 diretta verso le 7 sul quadrante dell'orologio. Questo procedimento di contrazioni e rotazioni successive viene chiamato «moltiplicazione» delle frecce.

Questo evento può essere considerato come una successione di due passi. Primo passo: un fotone va dalla sorgente fino al punto A, riflettendosi sull'unica superficie del blocco di vetro. Secondo passo: il fotone va da A fino al fotomoltiplicatore in C, riflettendosi sullo strato di vetro in B. A ciascun passo corrisponde una freccia risultante o, come si dice in linguaggio tecnico, una «ampiezza» (d'ora in avanti userò indifferentemente l'uno o l'altro dei due termini), che può essere calcolata sulla base delle regole già note. L'ampiezza relativa al primo passo ha lunghezza 0,2 (il cui quadrato è 0,04, la probabilità di riflessione su una singola superficie di vetro) ed è orientata secondo una certa direzione, poniamo come una lancetta che segni le 2.

Per calcolare l'ampiezza relativa al secondo passo, poniamo provvisoriamente la sorgente di luce in A in modo che i fotoni vengano diretti verso lo strato di vetro B. Disegniamo le frecce per la riflessione frontale e posteriore e sommiamole, ottenendo (mettiamo) una freccia risultante di lunghezza 0,3 diretta verso le 5 sul quadrante dell'orologio.

Come si devono combinare le due frecce per calcolare l'ampiezza per l'evento complessivo? Consideriamole da un punto di vista nuovo: come istruzioni per una contrazione e una rotazione.

Nel presente esempio la prima ampiezza ha lunghezza 0,2 ed è diretta verso le 2. Se si inizia con una «freccia unitaria», cioè con una freccia di lunghezza 1 diretta verso l'alto, la si deve accorciare da 1 a 0,2 e ruotare dalle 12 alle 2. L'ampiezza relativa al secondo passo la si può pensare come una contrazione della freccia unitaria da 1 a 0,3 e una sua rotazione dalle 12 alle 5.

Per combinare le ampiezze relative a entrambi i passi si deve procedere ad accorciare e ruotare in successione. Dapprima si accorcia la freccia unitaria da 1 a 0,2 e la si ruota dalle 12 alle 2, poi si accorcia la freccia così ottenuta da 0,2 a tre decimi di tale valore, e la si ruota dell'angolo compreso tra le 12 e le 5, cioè dalle 2 alle 7. La freccia risultante ha lunghezza 0,06 ed è diretta verso le 7. Essa rappresenta una probabilità data da 0,06 al quadrato, vale a dire 0,0036.

Osservando attentamente questo procedimento, si vede che il risultato di accorciare e girare in successione due frecce è lo stesso che sommare i rispettivi angoli (quello tra le 12 e le 2 + quello tra le 12 e le 5) e moltiplicare tra loro le lunghezze (0,2 × 0,3). È facile capire perché si sommino gli angoli: essi corrispondono alla rotazione della lancetta di un cronometro immaginario, e la rotazione per i due passi consecutivi è ovviamente la somma dell'angolo di cui la lancetta ha girato nel primo passo e di quello di cui ha girato nel secondo.

Soffermiamoci sul perché questo procedimento venga chiamato «moltiplicazione delle frecce»: è una spiegazione interessante. Proviamo per un momento a considerare la moltiplicazione dal punto di vista dei Greci (questa divagazione non ha nulla a che fare con l'argomento della lezione). Per poter usare numeri che non fossero interi i Greci li rappresentavano con dei tratti di linea. Ogni numero può essere espresso trasformando un tratto unitario mediante dilatazioni o contrazioni. Ad esempio, se la linea A rappresenta l'unità (fig. 38), la linea B rappresenta 2 e la linea C rappresenta 3.

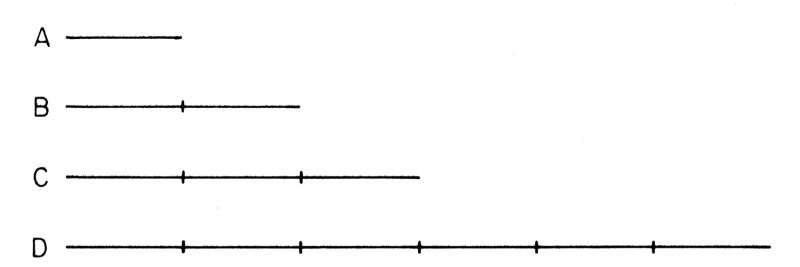
Fig. 38. Qualunque numero può essere ottenuto come trasformazione di un tratto unitario mediante contrazioni o dilatazioni. Se il tratto A rappresenta l'unità, B rappresenta 2 (dilatazione) e C rappresenta 3 (dilatazione). La moltiplicazione si ottiene tramite trasformazioni successive. Ad esempio, moltiplicare 3 per 2 significa dilatare la linea unitaria dapprima 3 volte e poi altre 2, ottenendo come risultato una dilatazione di 6 volte, rappresentata dalla linea D. Se si considera D come tratto unitario, il tratto C rappresenta 1/2 (contrazione) e il tratto B rappresenta 1/3 (contrazione). Moltiplicare 1/2 per 1/3 significa contrarre il tratto D prima a 1/2 e poi a 1/3 di tale risultato, ottenendo come risposta una contrazione a 1/6, rappresentata dal tratto A.

Come si fa a moltiplicare 3 per 2? Basta applicare le trasformazioni in successione: partendo dalla linea unitaria A, la si espande 2 volte e poi 3 volte (o 3 volte e poi 2 volte, l'ordine non fa alcuna differenza). Il risultato è la linea D, la cui lunghezza rappresenta 6. E per moltiplicare 1/3 per 1/2? Partendo da D come linea unitaria, la si accorcia prima a 1/2, ottenendo C, e poi a 1/3 di questa. Il risultato è la linea A, che rappresenta 1/6.

La moltiplicazione delle frecce funziona nello stesso modo (fig. 39). Si applicano trasformazioni in successione alla freccia unitaria, solo che le trasformazioni delle frecce coinvolgono due operazioni: contrazione e rotazione.

Fig. 39. I matematici hanno osservato che la moltiplicazione tra frecce può essere espressa come successione di trasformazioni di una freccia unitaria, nel nostro caso mediante contrazioni e rotazioni. Come nella comune moltiplicazione, l'ordine non è importante: si ottiene la stessa risposta, freccia X, moltiplicando la freccia V per W o W per V.

Per moltiplicare la freccia V per la freccia W, si contrae e si ruota la freccia unitaria dell'ammontare prescritto per V, poi si contrae e si ruota il risultato dell'ammontare prescritto per W; anche in questo caso l'ordine non fa differenza. Dunque la moltiplicazione delle frecce segue la stessa regola di trasformazione sequenziale che si applica ai soliti numeri.⁹

Torniamo al primo esperimento della prima lezione, la riflessione parziale su una singola superficie, avendo in mente questa idea dei passi successivi (fig. 40).

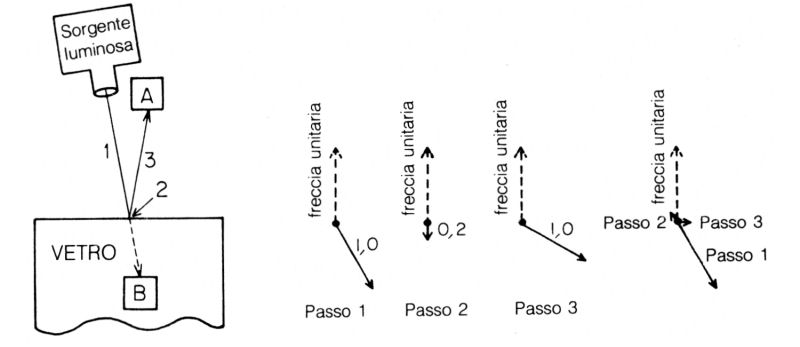
Fig. 40. La riflessione da una superficie singola può essere suddivisa in tre passi, ciascuno dei quali comporta una contrazione e/o una rotazione della freccia unitaria. Il risultato finale è lo stesso di prima: una freccia di lunghezza 0,2 che punta in una certa direzione, ma il nostro metodo di analisi risulta ora più dettagliato.

Possiamo dividere il percorso della luce in tre passi: 1) la luce va dalla sorgente al blocco di vetro, 2) è riflessa dal vetro, 3) va dal vetro al rivelatore. Ogni passo corrisponde a una determinata contrazione e rotazione della freccia unitaria.

Come ricorderete, però, in quella lezione non avevamo preso in considerazione tutti i percorsi che la luce può seguire nel riflettersi sul vetro. Ciò avrebbe richiesto di disegnare e sommare un'enorme quantità di piccole frecce e per evitare troppi dettagli ho dato l'impressione che la luce incida solo in un punto particolare, ossia che non si allarghi. In realtà, nel propagarsi da un punto a un altro, la luce si allarga (a meno che non si usi una lente) e ciò comporta una certa contrazione della freccia unitaria iniziale. Per il momento, tuttavia, manterrò il punto di vista semplificato secondo il quale la luce non si allarga, ed è quindi giustificato trascurare tale contrazione. È anche giustificato ammettere che, non essendovi allargamento, ogni fotone che parte dalla sorgente termina in A o in B.

Dunque, nel primo passo non c'è contrazione ma c'è rotazione, corrispondente all'angolo di cui ruota la lancetta del cronometro immaginario mentre il fotone viaggia dalla sorgente alla superficie frontale del vetro. Dopo il primo passo si ha pertanto una freccia di lunghezza 1 diretta, ad esempio, verso le 5.

Il secondo passo consiste nella riflessione del fotone da parte del vetro. In questo caso c'è una notevole contrazione, da 1 a 0,2 e una rotazione di mezzo giro. (Questi numeri sembrano per ora del tutto arbitrari: essi dipendono dal materiale su cui si riflette la luce, e nella terza lezione si vedrà da dove vengono). Il secondo passo è rappresentato da una freccia di lunghezza 0,2 che segna le 6 (mezzo giro).

Nel terzo passo il fotone viaggia dal vetro al rivelatore. Come nel primo passo, non c'è contrazione ma solo rotazione; supponiamo che la distanza percorsa sia leggermente più breve che nel primo passo e che la freccia si porti sulle 4.

Ora «moltiplichiamo» in successione le frecce 1, 2 e 3 (cioè sommiamo gli angoli e moltiplichiamo le lunghezze). Il risultato finale di questi tre passi, ossia l) rotazione, 2) contrazione e rotazione di mezzo giro, 3) rotazione, è lo stesso di quello trovato nella prima lezione: la rotazione dovuta ai passi 1 e 3 (dalle 12 alle 5 più dalle 12 alle 4) è la stessa di quella trovata lasciando che il cronometro seguisse il fotone per l'intera distanza (dalle 12 alle 9); il mezzo giro in più del passo 2 fa sì che la freccia punti nel verso opposto alla lancetta del cronometro, come accadeva nella prima lezione; infine la contrazione a 0,2 nel secondo passo produce una freccia il cui quadrato rappresenta una probabilità del 4% di riflessione parziale su una superficie singola.

In questo esperimento c'è un problema su cui non ci eravamo soffermati durante la prima lezione: che succede ai fotoni che vanno in B, cioè che attraversano la superficie del vetro? L'ampiezza per questo processo deve avere lunghezza circa 0,98, poiché 0,98 × 0,98 = 0,9604, che è ragionevolmente vicino al 96%. Anche questa ampiezza può essere analizzata riducendo il percorso in vari passi (fig. 41).

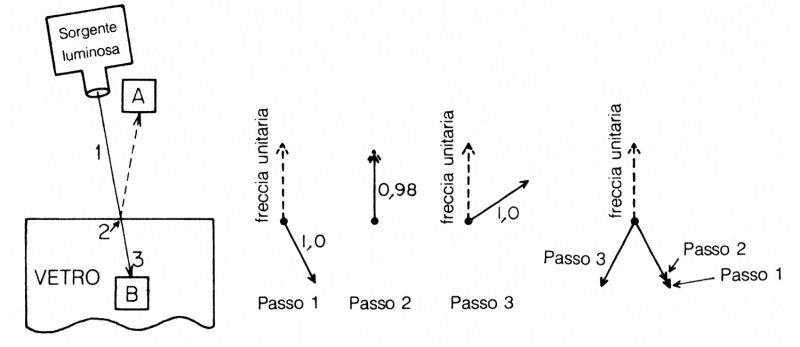
Fig. 41. Anche la trasmissione attraverso una singola superficie può essere suddivisa in tre passi, ciascuno dei quali comporta una contrazione e/o una rotazione. Il quadrato di una freccia di lunghezza 0,98 vale circa 0,96 e rappresenta una probabilità di trasmissione del 96% (che combinata con la probabilità di riflessione del 4% dà conto del 100% della luce).

Il primo di questi è uguale a quello del percorso che finisce in A: il fotone va dalla sorgente al vetro, e la freccia unitaria viene ruotata verso le 5.

Nel secondo passo il fotone attraversa la superficie del vetro: non vi è rotazione associata con tale passo, ma una piccola contrazione a 0,98.

Il terzo passo, la propagazione del fotone all'interno del vetro, comporta una ulteriore rotazione, ma nessuna contrazione.

Il risultato finale consiste in una freccia di lunghezza 0,98, con una direzione imprecisata, il cui quadrato, pari a 0,96, dà la possibilità che il fotone arrivi in B.

Consideriamo adesso nuovamente la riflessione parziale da due superfici. La riflessione sulla superficie frontale è la stessa che per una superficie singola, per cui i tre passi coincidono con quelli appena visti (fig. 40).

La riflessione sulla superficie posteriore può invece essere suddivisa in sette passi (fig. 42).

Fig. 42. La riflessione dalla superficie posteriore di una lamina di vetro può essere suddivisa in sette passi. I passi 1, 3, 5 e 7 consistono soltanto in una rotazione; i passi 2 e 6 consistono in una contrazione a 0,98 mentre il 4 consiste in una contrazione a 0,2. Come risultato si ha una freccia di lunghezza 0,192 (approssimata a 0,2 nella prima lezione) ruotata di un angolo corrispondente alla rotazione complessiva della lancetta del cronometro immaginario.

Essi comportano una rotazione pari alla rotazione totale della lancetta del cronometro che segue il fotone lungo l'intero percorso (passi 1, 3, 5 e 7), una contrazione a 0,2 (passo 4) e due riduzioni a 0,98 (passi 2 e 6). La freccia risultante avrà direzione corrispondente alla rotazione totale, come prima, e lunghezza circa 0,192 (= 0,98 × 0,2 × 0,98), arrotondata a 0,2 nella prima lezione.

Riassumendo, le regole che descrivono la riflessione e la trasmissione della luce da parte del vetro sono: 1) la riflessione dall'aria all'aria (sulla superficie frontale) comporta una contrazione a 0,2 e mezzo giro di rotazione; 2) la riflessione dal vetro nel vetro (sulla superficie posteriore) comporta anch'essa una contrazione a 0,2 ma nessuna rotazione; 3) il passaggio dall'aria al vetro o viceversa comporta una contrazione a 0,98 ma nessuna rotazione.

A rischio di farvi fare indigestione, non so resistere alla tentazione di discutere un altro bellissimo esempio di come si procede all'analisi di un fenomeno mediante tale suddivisione in passi successivi. Spostiamo il rivelatore sotto la lamina di vetro, e consideriamo un fatto non discusso nella prima lezione: la probabilità di trasmissione attraverso due superfici di vetro (fig. 43).

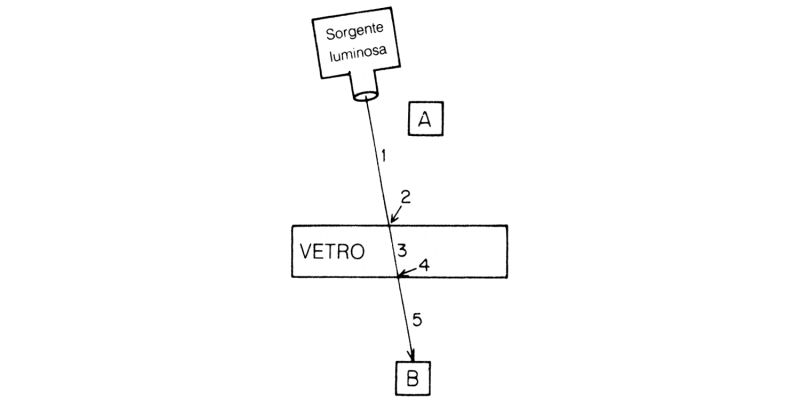
Fig. 43. La trasmissione attraverso due superfici può essere suddivisa in cinque passi. Il passo 2 provoca una contrazione a 0,98 della freccia unitaria, mentre il 4 fa contrarre al 98% la freccia lunga 0,98, ottenendo 0,96; i passi 1, 3 e 5 comportano solo rotazioni. Il quadrato della freccia risultante, lunga 0,96, vale 0,92 e rappresenta una probabilità di trasmissione attraverso due superfici del 92%, corrispondente all'8% di probabilità di riflessione che risulta corretto «due volte al giorno». Allorché lo spessore della lamina è tale da dar luogo a una probabilità di riflessione del 16%, col 92% come probabilità di trasmissione si ottiene il 108% della luce! Deve esserci qualcosa di sbagliato in questa analisi!

Naturalmente la risposta la sapete già: la probabilità che un fotone ha di arrivare in B è semplicemente il 100%, meno quella di arrivare in A, calcolata in precedenza. Così, se si fosse trovata una probabilità del 7% di arrivare in A, quella di arrivare in B sarebbe del 93%. Poiché la probabilità di arrivare in A varia da zero al 16%, a seconda dello spessore del vetro, quella di arrivare in B deve variare dal 100% all'84%.

Questa, certamente, è la risposta corretta, ma deve essere possibile calcolare qualunque probabilità come quadrato di una freccia risultante. Come si calcola la freccia della probabilità per la trasmissione attraverso uno strato di vetro? Come si accorda la sua lunghezza con quella della freccia per la riflessione verso A, così che la probabilità di finire in A più quella di finire in B sommino in ogni caso esattamente al 100%? Discutiamo la cosa un po' più in dettaglio.

Il percorso di un fotone che va dalla sorgente al rivelatore sotto il blocco di vetro, in B, può essere suddiviso in cinque passi. Vediamo come ruota e si contrae la freccia unitaria iniziale mentre il fotone procede.

I primi tre passi sono identici a quelli dell'esempio precedente: il fotone va dalla sorgente al vetro (rotazione ma non contrazione); attraversa la superficie frontale (nessuna rotazione e una contrazione al 98%); si propaga all'interno del vetro (rotazione ma non contrazione).

Il quarto passo, cioè l'attraversamento della superficie posteriore, è analogo al secondo: niente rotazione e ulteriore riduzione al 98%. A questo punto la freccia ha lunghezza 0,96.

Infine il fotone viaggia nuovamente nell'aria fino al rivelatore, e ciò comporta ancora rotazione ma nessuna contrazione. Il risultato finale è una freccia di lunghezza 0,96 diretta nella direzione determinata dalle varie rotazioni della lancetta del cronometro.

Una freccia lunga 0,96 rappresenta una probabilità di circa il 92% (0,96 al quadrato), il che significa una media di 92 fotoni che giungono in B su 100 che partono dalla sorgente. Ciò significa anche che l'8% dei fotoni sono riflessi dalle due superfici e arrivano in A. Ma nella prima lezione si era trovato che la riflessione dell'8% da due superfici si verifica solo in certi casi («due volte al giorno») e che in realtà essa oscilla ciclicamente da zero al 16%, al variare dello spessore della lamina di vetro. Cosa succede quando questo spessore è tale da produrre una riflessione del 16%? Su 100 fotoni emessi dalla sorgente 16 arrivano in A e 92 in B, sicché ci si ritrova col 108% della luce emessa — orrore! È chiaro che c'è qualcosa che non va.

Abbiamo dimenticato di tener conto di tutti i percorsi con cui la luce può giungere in B! Ad esempio, può rimbalzare sulla superficie posteriore, ripercorrere il vetro come per andare in A, ma poi riflettersi sulla superficie anteriore e tornare indietro verso B (fig. 44). Questo percorso richiede nove passi. Vediamo cosa accade alla freccia unitaria via via che la luce li compie (niente paura: si tratta solo di contrazioni e rotazioni!).

Fig. 44. Per rendere i calcoli più accurati occorre tener conto di un secondo modo in cui la luce può attraversare una lamina con due superfici Il percorso corrispondente comporta due contrazioni a 0,98 (passi 2 e 8) e due contrazioni a 0,2 (passi 4 e 6) e dà luogo a una freccia di lunghezza 0,0384 (arrotondata a 0,04).

Primo passo: il fotone viaggia nell'aria, si ha rotazione ma non contrazione. Secondo passo: il fotone attraversa la superficie del vetro, niente rotazione ma contrazione al 98%. Terzo: il fotone viaggia nel vetro, rotazione ma non contrazione. Quarto: riflessione sulla superficie posteriore, niente rotazione ma la freccia si contrae allo 0,2 di 0,98, cioè a 0,196. Quinto: il fotone torna indietro nel vetro, solo rotazione. Sesto: il fotone rimbalza sulla superficie frontale, che si comporta come superficie «posteriore», poiché il fotone arriva dall'interno del vetro, per cui non si ha rotazione ma una contrazione allo 0,2 di 0,196 cioè a 0,0392. Settimo: il fotone ripercorre il vetro, ancora rotazione. Ottavo: il fotone attraversa la superficie posteriore, niente rotazione ma ulteriore contrazione al 98% di 0,0392 cioè a 0,0384. Infine, nono passo: il fotone si propaga nell'aria e arriva al rivelatore, ancora rotazione ma nessuna contrazione.

Il risultato di tutte queste contrazioni e rotazioni è una freccia di lunghezza 0,0384 (che si può porre uguale a 0,04) orientata nella direzione dell'immaginaria lancetta di cronometro che ha seguito il fotone in questo lungo viaggio. Questa freccia corrisponde a un secondo modo in cui la luce può arrivare dalla sorgente al rivelatore. Avendo due percorsi, per trovare la freccia finale si devono ora sommare le ampiezze corrispondenti al percorso più diretto, la cui lunghezza è 0,96, e a quello più lungo, che ha lunghezza 0,04.

Le due frecce di solito non hanno la stessa direzione, e il cambiare lo spessore del vetro modifica la loro direzione relativa. Ma si osservi come tutto torna: la rotazione della lancetta che segue il fotone durante i passi 3 e 5 del percorso verso A è esattamente uguale a quella corrispondente ai passi 5 e 7 del percorso verso B. Ciò comporta che quando le due frecce relative alla riflessione si cancellano, dando luogo a una freccia finale che rappresenta riflessione nulla, le frecce relative alla trasmissione si rinforzano dando una freccia finale di lunghezza 0,96 + 0,04 = 1; quando la probabilità di riflessione è nulla, quella di trasmissione è del 100% (fig. 45).

Viceversa, quando le frecce per la riflessione si rinforzano dando un'ampiezza di 0,4, quelle della trasmissione sono dirette in versi opposti, dando una freccia di lunghezza 0,96—0,04 = 0,92; calcolando le probabilità (cioè i quadrati), si ottiene 16% per la riflessione e 84% per la trasmissione. E così la Natura, con le sue regole intelligenti, dà sempre ragione del 100% dei fotoni!¹⁰

 

Fig. 45. La Natura fa sempre in modo di dar conto del 100% della luce. Quando lo spessore è tale che le frecce relative alla trasmissione si addizionano, quelle relative alla riflessione si elidono; se le frecce relative alla riflessione si addizionano, quelle della trasmissione sono opposte tra loro.

Fig. 46. Per fare un conto ancora più accurato bisognerebbe prendere in considerazione ancora altri percorsi che la luce può seguire per riflettersi. In quello mostrato in figura si ha una contrazione a 0,98 nei passi 2 e 10, e a 0,2 nei passi 4, 6 e 8. Come risultato si ha una freccia lunga circa 0,008 relativa a un possibile percorso che produce riflessione, e che va quindi sommata alle altre frecce relative alla riflessione (quella «frontale», lunga 0,2, e quella «posteriore», lunga 0,192).

Prima di terminare questa lezione, voglio far osservare che la regola sulla moltiplicazione delle frecce deve essere generalizzata; si devono moltiplicare tra loro le frecce non solo per i fenomeni che consistono di vari passi, ma anche per i fenomeni formati da più eventi che avvengono in modo indipendente e contemporaneo. Supponiamo, ad esempio, di avere in X e in Y due sorgenti e in A e in B due rivelatori (fig. 47), e di voler calcolare la probabilità del seguente fenomeno: X e Y emettono entrambe un fotone e A e B ne acquistano entrambi uno.

I fotoni viaggiano liberamente fino ai rivelatori, senza riflessioni o trasmissioni da un mezzo a un altro; perciò questo è il momento adatto per prendere finalmente in considerazione il fatto che la luce si allarga mentre si propaga. Discuterò pertanto la regola completa che descrive la propagazione della luce monocromatica nello spazio vuoto, senza più approssimazioni o semplificazioni. A parte la polarizzazione, questa regola è tutto ciò che occorre sapere sulla luce monocromatica che viaggia nello spazio vuoto. Essa afferma che la direzione della freccia è quella dell'immaginaria lancetta di cronometro che ruota un certo numero di volte per centimetro percorso (a seconda del colore del fotone), mentre la sua lunghezza è inversamente proporzionale alla distanza percorsa dalla luce, in altre parole la freccia si accorcia man mano che la luce si propaga.¹¹

Supponiamo che la freccia per andare da X ad A abbia lunghezza 0,5 e segni le 5, e che lo stesso valga per la freccia per andare da Y a B (fig. 47). Moltiplicandole tra loro si ottiene una freccia risultante di lunghezza 0,25 orientata verso le 10.

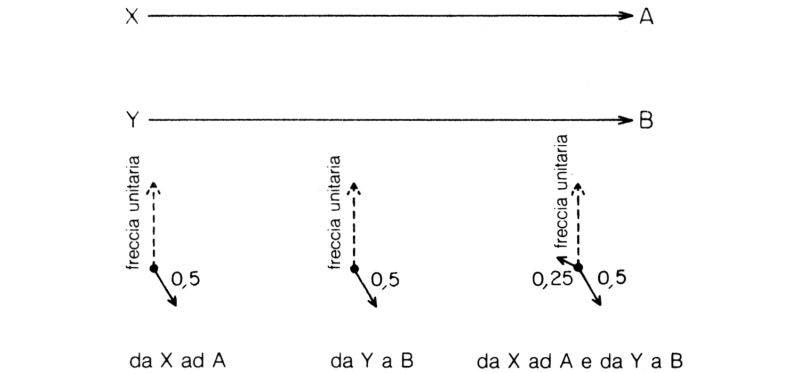
Fig. 47. Se un determinato fenomeno può verificarsi in un modo che dipende da un insieme di eventi indipendenti, l'ampiezza relativa a tale modo va calcolata moltiplicando tra loro le frecce relative ai singoli eventi indipendenti. Nella figura è illustrato il seguente fenomeno: dopo che ciascuna delle due sorgenti X e Y ha emesso un fotone, entrambi i fotomoltiplicatori in A e in B scattano. Tale fenomeno può verificarsi se un fotone va da X ad A mentre un altro va da Y a B (due eventi indipendenti). La probabilità relativa a questo «primo modo» va calcolata moltiplicando tra loro le frecce per ciascun evento indipendente (un fotone da X ad A e uno da Y a B), ottenendo così l'ampiezza relativa a questo modo specifico (l'analisi continua con la fig. 48).

Un momento! Questo fenomeno può avvenire anche in un altro modo: il fotone di X va in B, mentre quello di Y va in A. Ciascuno di questi eventi ha una propria ampiezza, e le relative frecce vanno moltiplicate tra loro per ottenere l'ampiezza corrispondente a questo altro modo (fig. 48). Le lunghezze delle singole frecce sono molto vicine al caso precedente, essendo le distanze percorse quasi uguali, cioè le frecce per andare da X a B e da Y ad A hanno praticamente lunghezza 0,5; molto diversa da prima sarà invece la loro direzione: la lancetta del cronometro compie 14.000 giri al centimetro per la luce rossa, per cui anche una piccola differenza nel tragitto comporta una notevole differenza nella direzione della freccia.

Le ampiezze relative a questi due modi vanno ora sommate per ottenere la freccia finale. Avendo essenzialmente la stessa lunghezza, le due frecce si cancellano tra loro se hanno direzioni opposte. La loro direzione relativa può essere modificata cambiando la distanza tra le sorgenti o tra i rivelatori: allontanare o avvicinare tra loro un pochino i rivelatori può aumentare la probabilità dell'evento o viceversa renderla nulla, proprio come nel caso della riflessione parziale su due superfici.¹²

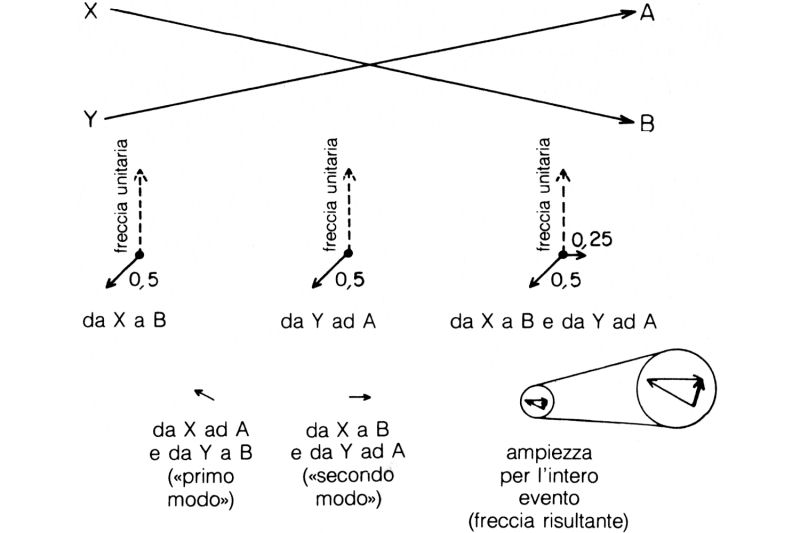
Fig. 48. L'altro modo in cui può verificarsi il fenomeno descritto alla fig. 47: il fotone di X va in B, mentre quello di Y va in A. Anche questo modo dipende dal verificarsi contemporaneo dì due eventi indipendenti, per cui anche l'ampiezza relativa a questo «secondo modo» va calcolata moltiplicando tra loro le frecce relative ai due eventi indipendenti. Le frecce per il «primo» e per il «secondo» modo vanno poi sommate tra loro, per avere la freccia risultante per il fenomeno considerato. La probabilità di un evento è sempre rappresentata da una singola freccia finale, indipendentemente dal numero delle frecce tracciate, moltiplicate e sommate per ottenerla.

In questo esempio si sono prima moltiplicate delle frecce tra loro, poi si sono sommati i risultati per ottenere la freccia finale (l'ampiezza dell'evento) il cui quadrato dà la probabilità dell'evento.

Occorre sottolineare che qualunque sia il numero di frecce tracciate, moltiplicate o sommate, l'obiettivo finale è sempre quello di calcolare una sola freccia risultante relativa al fenomeno. Gli studenti di fisica fanno spesso degli errori all'inizio, perché non tengono presente questo punto fondamentale. Passano tanto di quel tempo ad analizzare eventi in cui interviene un singolo fotone, che cominciano a pensare che la freccia sia in qualche modo associata al fotone. Ma le frecce sono solo ampiezze di probabilità, e il loro quadrato dà la probabilità di un evento completo.¹³

Con la prossima lezione comincerò il processo di semplificazione e spiegazione delle proprietà della materia, in modo da mostrare l'origine dei vari fenomeni discussi: la contrazione a 0,2, il fatto che la luce sembra andare più lenta nel vetro e nell'acqua che nell'aria, eccetera. Perché finora io ho barato: i fotoni in realtà non rimbalzano sulla superficie del vetro, ma interagiscono con gli elettroni al suo interno. Farò vedere che i fotoni non fanno altro che viaggiare da elettrone a elettrone e che riflessione e trasmissione altro non sono che il risultato di tante interazioni in cui un elettrone prende un fotone, ‘si gratta la testa’, per così dire, ed emette un nuovo fotone. Questa semplificazione di tutti i fenomeni di cui ho parlato finora è veramente molto bella.