-
Alignments are hypotheses of positional homologies between nucleotides or amino acids of sequences.
-
The Needleman and Wunsch algorithm finds the optimal pairwise alignments of two sequences, which can contain matches, mismatches and gaps.
-
Local alignments optimize the positional homology for substrings of sequences and are widely used in database searches.
-
Multiple sequence alignments can only be retrieved using heuristic approaches, e.g. progressive alignments.
-
Alignment masking is the exclusion of unreliably aligned positions to improve the signal-to-noise ratio of the data.
-
Mapping of sequence reads to reference sequences is a special case of alignments; most mapping algorithms are either based on a seed-and-extend approach or Burrows-Wheeler transform-related methods.
6.1 Pairwise Alignment
Homology is broadly defined as a
character that arises as a result of common ancestry (Thornton and
DeSalle 2000). Homologies can be
hypothesized at different levels. For phylogenomics it is important
to establish the homology of genes (or genomic regions), but also
the homology of nucleotide or amino acid positions within genes (or
genomic regions). Alignments are hypotheses of positional
homologies between the nucleotides or amino acids of sequences
(Rosenberg 2009) and can be either
global or local (Phillips et al. 2000). In a global alignment, positional
homology across all positions of two aligned sequences is
determined. Global alignments are used for phylogenetic analyses or
to detect patterns of selection. In contrast, for local alignments
positional homology is optimized only for fragments (substrings) of
two sequences. Local alignments are widely used for database
searches as, for example, implemented in the BLAST algorithm (see
below). In general, it is possible to align any two sequences and
there are many possibilities to do this. To compare different
sequence alignments, it is necessary to use a metric to estimate
the quality of each alignment.
In an alignment the horizontal rows
are sequences, whereas the vertical rows represent characters which
refer to positions in a sequence. The residues of the sequence
itself are used as character states. There are four different
character states for nucleotide sequences and 20 different
character states for amino acid sequences. If a character of two
aligned sequences shows the same character state, it is called a
match, whereas the presence of different character states within a
character is called mismatch (◘ Fig. 6.1). Additionally it is
possible that gaps are inserted into alignments (◘ Fig.
6.1). These
gaps represent either events of insertions in one sequence or a
deletion in the other sequence. Often it is neither simple nor
necessary to determine which of the events took place, and they are
together summarized as indels (Simmons and Ochoterena
2000).


Fig.
6.1
Global alignment of two sequences. Matched
base pairs, mismatches and gaps are exemplified. Scoring matches
with +1 and mismatches and gaps with −1 results in a total score of
+3
To estimate the quality of a pairwise
alignment, a simple score can be developed, where the number of
matched base pairs is scored as a benefit, whereas the number of
mismatches and gap positions induces costs. Generally, the goal is
to maximize the benefits while minimizing the costs. For example,
scores could be arbitrarily set as follows: match +1, mismatch −1
and gap −1. The alignment in ◘ Fig. 6.1 has ten matches, five
mismatches and two gap positions, which results into a score of +3.
An alternative alignment of the same two sequences is given in
◘ Fig. 6.2.
This alignment only contains matches and gap positions. Even though
the number of matches is higher than the alignment given in ◘ Fig.
6.1, the total
score of 0 is lower. Comparing these two alignments, the
alternative in ◘ Fig. 6.1 would be chosen as the better one, as it has
the higher score given our introduced scoring system.


Fig.
6.2
A different pairwise sequence alignment
with the same sequences as in ◘ Fig. 6.1. Scores for matches
and gaps are given below each sequence position; the combined score
is 0
Of course the used scoring system is
arbitrary, and a different one may support the choice of an
alternative alignment. Especially the scoring of gap characters has
been debated (Giribet and Wheeler 1999). Gaps have obviously to be introduced when
aligning two sequences of different lengths. Gaps are resulting
from a different biological process than mismatches. Whereas
mismatches (mostly) trace back to mutations, gaps are the result of
indels. Possible mechanism for indels are errors during DNA
replication (e.g. slipped-strand mispairing), unequal crossing over
during recombination or introduction of mobile elements (McGuffin
2009; Levinson and Gutman
1987). All these mechanisms
usually result in the simultaneous insertion (or deletion) of
sequences, which implies that multiple neighbouring gaps stem from
a single event. Using a scoring system that treats all gaps
independently would therefore introduce an over-penalization for
them, as implicitly separate events would be assumed for their
origin (McGuffin 2009). As a
solution to this problem, the use of affine gap costs has been
introduced. This type of penalty differentiates between opening a
gap and extending it. For example, using gap opening costs of −1
and gap extension costs of 0.1 for ◘ Fig. 6.2 would result in a
total score of +5.4, whereas the alignment in ◘ Fig. 6.1 remains at +3.
Similarly, it is possible to introduce different scores for
mismatches. For example, in case of aligning protein sequences,
scores are usually based on matrices that incorporate the
evolutionary preferences for certain substitutions over other kinds
of substitutions. Widely used matrices are BLOSUM and PAM (Henikoff
and Henikoff 1992). ◘ Figure
6.3 shows the
BLOSUM62 matrix (Henikoff and Henikoff 1992), which is used by all BLAST searches (see
below) on an amino acid level. Scores in these matrices are given
as log-odds, which can be directly used as parameters of alignment
scoring schemes. Positive scores mean that we find amino acid
pairings more often than expected by chance (conservative
substitutions); negative values indicate those occurring less often
as expected (non-conservative substitutions) (Eddy 2004). Alternatively, a matrix counting the
steps for amino acid substitutions inferred from the genetic code
can be implied. In this case, costs are either −1 (one change in
the codon triplet needed), −2 (two changes needed) or −3 (three
changes needed). Obviously, choice of the scoring function and its
parameters has a huge influence on selecting the best pairwise
alignment.


Fig.
6.3
BLOSUM62 matrix giving log-odd scores for
each possible amino acid substitution derived from pairwise
sequence alignments of at least 62% identity
To find the best optimal alignment, it
would be necessary to compare all possible pairwise alignments,
which can be a giant number given that it grows faster than
exponentially with increasing sequence length. However, a simple
solution finding the optimal pairwise global alignment was
published by Needleman and Wunsch (1970). This method is a dynamic programming
approach, where to solve a complex problem is broken down into more
simple and thereby easy-to-solve subproblems (Cooper and Cooper
1981). The Needleman and Wunsch
algorithm consists of three steps: matrix initialization, matrix
filling and traceback. In the first step, a matrix is initialized,
containing the two sequences along an axis (◘ Fig. 6.4). Additionally, an
empty row is added to the top and an empty column to the left of
the matrix. Next, a zero is placed in the upper left corner, and
the top row and the left column are filled with increasing
multiples of the costs for a gap. Moreover, arrows are introduced
into each of these cells, pointing to the zero in the upper left.


Fig.
6.4
Initialization of a matrix for the
Needleman and Wunsch (1970) global
alignment algorithm. The first row and column are filled with
increasing multiples of the gap cost and arrows pointing to 0
The second step is filling the matrix.
Given the chosen scoring system, three values are calculated for
every single cell (◘ Fig. 6.5): match/mismatch score, vertical gap score
and horizontal gap score. The match/mismatch cost (M) equals the
sum of the value of the cell that is diagonally to the upper left
plus costs for a match or mismatch (whatever applies). The
horizontal gap score equals the sum of the value of the cell to the
left plus the gap score. The vertical gap score equals the sum of
the value of the cell above it plus the gap score. The highest
value is chosen to fill the box, and an arrow indicates where it
comes from. In the case of equally high values, multiple arrows can
be introduced or one of the solutions is chosen randomly.


Fig.
6.5
Filling of the matrix. Using the chosen
scoring system, three values are calculated for each box. The
match/mismatch cost (M) is the sum of the value of the cell that is
diagonally to the upper left (0) plus costs for a match (in this
example, it can be also mismatch) (+1) which totals +1. The
horizontal gap score is the sum of the value of the cell to the
left (−1) plus the gap score (−1), which totals −1. The vertical
gap score is the sum of the value of the cell above it (−1) plus
the gap score (−1). The highest value is chosen to fill the box,
and an arrow indicates
where it comes from
The last step is the traceback, where
starting with field in the bottom right, the path of the arrows is
followed to the upper left (◘ Fig. 6.6). Following a diagonal
arrow means that residues from the row and the column of this field
should be aligned. In case of following a vertical arrow, a residue
of the vertical (upper sequence) is aligned with a gap, whereas in
the case of following a horizontal arrow, the gap is placed in the
other sequence. If multiple arrows were introduced during the
filling, equally optimal alignments can be retrieved.


Fig.
6.6
The traceback uncovers the (or one) optimal
alignment. Starting with field in the bottom right, the path of the
arrows is followed to the upper left. The arrows indicate if bases
should be matched (diagonal
arrows), gaps should be included in the upper sequence
(arrow pointing upwards) or
gaps should be introduced in the sequence to the left (arrow pointing left)
The dynamic programming for global
alignments can be formalized (when using linear gap costs) as a
recursion, where the maximal score F(i,j) is calculated between the first
i residues of sequence
X and the first
j residues of sequence
Y. The recursion of the
Needleman and Wunsch (1970) algorithm looks as follows:

First, the score for the last
alignment column is calculated, which is either s(Xi,Yj) in case of matching
(mismatching) base pairs or –g when a gap is included in either of
the sequences. The score of each of the remaining alignment columns
is F(i,j), F(i-1,j) or F(i,j-1), depending on which of the
alternatives applies. The score of the optimal alignment is the sum
of the scores of the alignment columns (Morgenstern 2009). Many computational tools for pairwise
sequence alignment are available. For example, an online tool for
DNA and protein alignments based on this algorithm can be found on
the website of the EMBL-EBI (► http://www.ebi.ac.uk/Tools/psa/)
(Rice et al. 2000).
6.2 Local Alignment and BLAST Searches
Local alignments can be used to find
similarities (and putative homologies) between fragments
(substrings) of two sequences. Typical applications are database
searches to retrieve most similar sequences (sequence fragments)
for the input sequence. At the beginning, the task for a local
pairwise alignment looks to be more complex as for global pairwise
alignments, as it basically means performing many different global
alignments for different starts and ends of the compared
substrings. Fortunately, Smith and Waterman (1981) proposed a computationally easy solution
for this problem based on an adaptation of the Needleman and Wunsch
(1970) algorithm (NWA). Similarly
to the latter algorithm, a matrix is created based on the length of
the sequences, and all cells are filled based on a scoring system
(◘ Fig. 6.7).
However, the extra row and column directly at the upper and left
border of the matrix are now filled with zeros. During the fill-in,
the cells of the matrix are filled with the same rules as in the
NWA, with the exception that always when a negative value is
calculated, the cell is filled with a zero instead. Moreover,
arrows are only assigned in case they point towards a positive
value. The final traceback starts at the highest values within the
matrix, following the arrows till a zero is reached (◘ Fig.
6.7).


Fig.
6.7
Completed matrix using the Smith and
Waterman (1981) algorithm. The
traceback starts at the highest value of the matrix and only
substrings of the sequences are aligned
The computation time of the Smith and
Waterman (1981) algorithm (SWA)
grows linearly with the product of the length of the two compared
sequences (Cristianini and Hahn 2007). While this is a relatively fast approach,
it is still computationally too resource intensive for standard
database search applications. For example, a common task is to find
the most similar sequences of a given query in a public database.
Usually, all published sequence data are stored in one of the three
main databases: NCBI GenBank, EMBL-Bank of the European Molecular
Biology Laboratory or in the DNA Data Bank of Japan (DDBJ) (Pevsner
2015). All these databases share
their data daily. NCBI GenBank is hosted by the National Institutes
of Health (NIH) in the USA, which keeps an annotated collection of
all publicly available DNA sequences (Benson et al. 2013). In February 2016 (Release 212.0), GenBank
comprised 207,018,196,067 bases from 190,250,235 reported sequences
in its sequence database. Additionally, billions of sequences from
NGS high-throughput platforms are stored in the sequence read
archive. Faster database search algorithms are needed to handle
these huge numbers of sequences. Two prominent algorithms which
have been developed are FASTA and BLAST. Both methods use
heuristics to identify regions of high similarity before
calculating pairwise alignment scores. FASTA (Lipman and Pearson
1985) is nowadays mostly known for
the underlying sequence format, which became a standard in
molecular sequence analyses. However, the by far most popular
method to search in extremely large databases is the BLAST
algorithm (Altschul et al. 1990).
BLAST is an acronym for Basic Local Alignment Search Tool. In
contrast to dynamic programming, it does not guarantee to find the
optimal alignment, as it uses a heuristic approach. However, it is
by two orders of magnitudes faster than the Smith and Waterman
algorithm, which is achieved by only searching within the sequence
space of high similarity.
BLAST searches start by finding all
words (k-mers) of a length
k (typically 3 for amino
acids and 11 for nucleotides), which exist in the query sequence
(◘ Fig. 6.8a).
Additionally, based on a substitution matrix, similar high-scoring
words (neighbourhood words) are listed for each word of the query
matrix. For example, in the example in ◘ Fig. 6.8, the word LEH is
derived from the query sequence. Similar words from its
«neighbourhood» are aligned (e.g. LKH, CEH, QEH, etc.) and ordered
according to its alignment score as calculated by using a
substitution matrix. For amino acid substitutions, the BLOSUM62
matrix (◘ Fig. 6.3) is usually used. A list of all words
retrieved by this procedure is stored, and exact matches of these
words in the database sequences are searched for (◘ Fig.
6.8b). Every
match is called a «high-scoring sequence pair» (HSP), which is used
as «seed» for local sequence alignment (◘ Fig. 6.8c). The alignment is
extended to the left and the right of the seed, and the alignment
score is calculated after every extension based on the substitution
matrix. The algorithm stops extending the alignment once the score
decreases by a fixed value X from the maximum score found at any
point during alignment. The final score for each local alignment is
kept, and all alignments with a score below a threshold value S are
discarded. BLAST has been initially developed for un-gapped
alignments (Altschul et al. 1990),
but is also available for alignments including gaps (Altschul et
al. 1997).


Fig.
6.8
Schematic representation of the workflow of
the BLAST algorithm. a A list
of words is derived from a query sequence. Additionally, for each
word high-scoring similar words based on a distance matrix (e.g.
BLOSUM62 for amino acids) are stored. b The complete list of words is used to
find exact matches in the database sequences. c Starting from the exact match, the
alignment is extended (in both directions) to find alignments with
scores above a given threshold
Based on the type of query sequence
and the type of chosen database, there are five variations of BLAST
searches. BLASTN uses nucleotide sequences as query to search
within a nucleotide database. BLASTP uses amino acid sequences as
query to search within a protein database. For BLASTX a nucleotide
query is translated in all six possible reading frames to be
compared with a protein database. TBLASTN compares a protein query
against a nucleotide database which is translated in all six
reading frames. And TBLASTX uses a nucleotide query translated in
all six reading frames to compare it on the amino acid level
against a nucleotide database, which is also translated in all six
reading frames. When targeting protein-coding genes, it is in most
cases advisable to use a BLAST algorithm that compares sequences on
an amino acid level. The BLAT algorithm is an alignment tool
similar to BLAST (Kent 2002). It
can be used to search genome assemblies for sequences of high
similarity. BLAT of DNA is designed to quickly find sequences with
a similarity greater than 95% and of a length of 40 bases or more.
Therefore it is commonly used to identify the location of a
sequence in the genome or determine the exon structure of an
mRNA.
Hits retrieved from BLAST searches can
be ordered according to their alignment score or using an
expectation value (e-value). The alignment score is calculated
based on pairwise alignments of the retrieved similar sequence
fragments. The e-value describes the number of hits we would expect
to find by chance (Cristianini and Hahn 2007). The lower the number, the more
significant is the hit. For example, an e-value of 1 means that at
least one hit of similar sequence length and sequence similarity is
to be expected by chance. Because the size of the database itself
is included in the calculation, very short sequences will always
have quite high e-values, even if there are 100% identical hits in
the database. BLAST searches can be performed by stand-alone
software using a command line or in a browser by several web
applications (e.g. ► http://blast.ncbi.nlm.nih.gov/Blast.cgi).
The output of BLAST searches are lists of sequences, ordered by
similarity. Typical output formats are pairwise outputs including
alignments (◘ Fig. 6.9a) or tabular outputs (◘ Fig. 6.9b). The latter are more
practical for phylogenomic applications, as all relevant
information can be easily parsed using scripts or command line
tools.
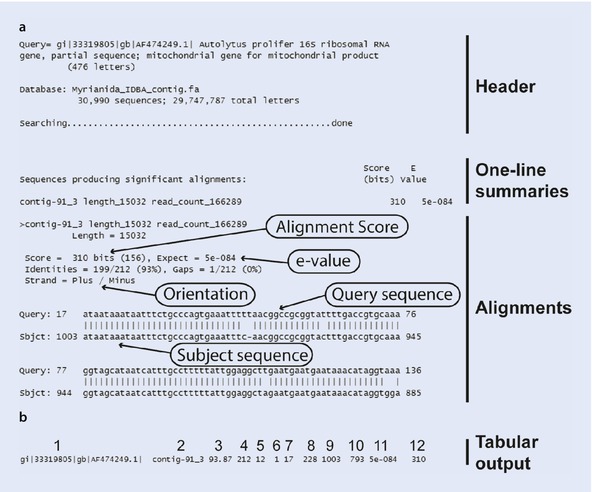

Fig.
6.9
Typical output of local BLAST searches.
a Pairwise output consisting
of header, one-line summary and alignments. b Tabular output in 12 columns: 1, query
sequence ID; 2, subject sequence ID; 3, percent identity; 4,
alignment length; 5, mismatches; 6, gaps; 7, query sequence
alignment start; 8, query sequence alignment end; 9, subject
sequence alignment start; 10, subject sequence alignment end; 11,
e-value; 12, alignment score
6.3 Multiple Sequence Alignment
Alignments of more than two sequences
are needed to resolve phylogenies of genes or species. Principally,
the Needleman and Wunsch algorithm introduced in 6.1 could be
extended to the problem of multiple sequence alignments (MSAs)
(Chan et al. 1992). In this case
the matrix would become multidimensional, and the algorithm would
work successively through each dimension. This approach is an
exhaustive method and would guarantee finding an optimal alignment.
However, the costs in terms of computation time increase
exponentially with the number of sequences and sequence length,
thereby limiting the usefulness of such an approach to cases with
very few sequences (Edgar and Batzoglou 2006). Instead, heuristic approaches with
reduced computational time are normally used for MSA. The most
popular approach is known as progressive alignment, developed by
Feng and Doolittle (1987). This
approach decomposes MSA into a series of pairwise sequence
alignment operations. Using a phylogenetic guide tree (e.g. a
neighbour-joining tree based on the pairwise distances derived from
pairwise alignments), the MSA is constructed by adding sequences
individually. Each node of the guide tree represents a separate
pairwise alignment, and the most similar sequences are added first,
and more distant sequences are added gradually (Phillips et al.
2000). By using this approach,
incongruent placement of gaps in pairwise alignments can severely
affect the quality of the corresponding MSA. Several methods
performing an iterative refinement have been developed to correct
placement of inconsistent gap positions and other problems in the
final MSA.
A phylogeny-aware method treating
indels as evolutionary distinct events was developed to increase
alignment quality (Löytynoja and Goldman 2008). However, this method seems to be rarely
used for phylogenomic studies, and alignment lengths are usually
greatly inflated by excessively introducing gaps. Whereas recent
phylogenomic analyses are mostly based on protein-coding genes (and
therefore amino acid alignments), phylogenetic studies using single
genes are often performed using the small (eukaryotes) or large
(Bacteria and Archaea) ribosomal subunit, which are structural
genes exhibiting a secondary (and tertiary) structure (Cole et al.
2009). For this case, several
alignment programs using secondary structure models of ribosomal
genes to guide the alignment are available (Gardner et al.
2005).
The most widely used software for MSA
has been CLUSTAL W, which was introduced in the mid-1990s (Thompson
et al. 1994). However, several
newer alignment programs are not only faster, but often also more
accurate: MAFFT (Katoh and Standley 2013), MUSCLE (Edgar 2004) or T-COFFEE (Notredame et al.
2000), to name the most popular.
Some benchmark datasets based on alignments of different complexity
(domain organization, mixture of conserved and non-conserved
regions) have been constructed and used to test the speed and
accuracy of different aligners (Thompson et al. 2005; Thompson et al. 2011). Generally, the tested alignment programs
work well. However, often different programs excel for different
problems. For example, some programs are better suited to align
conserved sequence blocks, whereas others are better in aligning
strongly diverging sequences (Thompson et al. 2011).
6.4 Alignment Masking
For sequence alignments it is not
unusual that some regions are aligned with more confidence than
others. For example, protein-coding genes often comprise one or
more conserved domains which are easier to align than flanking
regions. In the case of ribosomal genes, conserved regions and more
variable expansion regions differ in their degree of variability
and thereby in the confidence how regions can be aligned. Different
alignments mean different hypotheses of positional homology, and it
is long known that this can affect the resulting phylogenies
(Morrison and Ellis 1997; Thorne
and Kishino 1992). Likewise, also
other estimates as, for example, model parameters or inference of
positive selection might be heavily influenced by the accuracy of
the underlying alignment (Privman et al. 2012; Wong et al. 2008). As already mentioned every set of
characters can be aligned somehow. Alignments of random data have
been shown to bear phylogenetic signal resulting in supported tree
topologies (Hillis and Huelsenbeck 1992). Moreover, different alignment methods
seem to differ in their bias of creating artificial phylogenetic
resolution from random sequence data (Simmons et al. 2010). Furthermore, several similar optimal
solutions to the recovered alignment exist. In case of multiple
alignments using heuristics, it is not even guaranteed to find the
optimal solution. Not surprisingly, the most used alignment
algorithms differ in ~20% of the aligned positions when aligning
the same set of sequences in normal and reverse order (Landan and
Graur 2007). In summary, difficult
sequence alignments will usually always contain parts of ambiguous
positions and random similarity. As a solution to all these
problems, several studies proposed to mask and exclude unreliably
aligned positions of sequence alignments and thereby improve the
signal-to-noise ratio of the data.
Initially, alignment masking has been
often performed manually, which, however, has been strongly
criticized as irreproducible (Landan and Graur 2007) and is also not possible when dealing with
hundreds of genes. Several programs for automatic and reproducible
alignment masking have been published, and some of the most widely
used are GBLOCKS (Castresana 2000;
Talavera and Castresana 2007),
SOAP (Löytynoja and Milinkovitch 2001), AL2CO (Pei and Grishin 2001), MUMSA (Lassmann and Sonnhammer
2005), ALISCORE (Misof and Misof
2009), GUIDANCE (Penn et al.
2010a) and ZORRO (Wu et al.
2012).
GBLOCKS was one of the first available
alignment maskers and is still widely used. By calculating the
degree of conservation of every single alignment position,
conserved «blocks» are identified. These «blocks» are retained for
further analyses based on a set of rules that can be modified by
the user. For example, a higher number of gap positions are allowed
or poorly conserved regions which are flanked by conserved ones can
be kept. Even though GBLOCKS has been criticized for using
arbitrary rules without theoretical justification, comparisons with
other alignment maskers based on simulated datasets show that this
software works well when parameters are carefully chosen (Kück et
al. 2010; Talavera and Castresana
2007). In contrast, other
alignment maskers explicitly use hidden Markov models or resampling
techniques to identify noisy alignment positions for exclusion.
ALISCORE uses parametric Monte Carlo resampling to identify
positions with random signal in multiple sequence alignments.
Therefore, an expected similarity score is generated for pairwise
alignments of randomized sequences within a sliding window. In the
case of nucleotide data, a scoring function based on matches and
mismatches is used to generate the similarity score, whereas for
amino acid, data scores of randomized sequences are derived from an
empirical matrix (e.g. BLOSUM62, see above). For nucleotide
sequences scores are adapted to varying base composition along
sequences and among sequences, whereas for amino acid data, this is
only calculated once based on the composition of the original data.
For the defined sliding window (e.g. 5 bps) of the original
alignment, the observed score is calculated as the sum of all
single-position comparisons, thereby calculating scores for all
sequence pairs. Finally, the observed score of the selected window
of the sequence alignment is compared with the expected score from
randomized sequences. For this comparison a frequency distribution
of random scores is generated, where randomness is assumed if the
observed score fails to be better than 95% of the scores from the
random sequences, generated by Monte Carlo resampling (Kück et al.
2010; Misof and Misof
2009). ZORRO measures the quality
of each individual alignment position by using a pair-hidden Markov
model (pair-HMM) (Wu et al. 2012).
Using this approach the quality of two aligned residues is
estimated in the context of all possible pairwise alignments. The
rational of the ZORRO algorithm is that if two residues are truly
homologous, they should also align in most of the alternative
pairwise alignments. Using pair-HMM (Bradley et al. 2009), the posterior probability of two positions
being aligned in all possible alignments is calculated. If the
posterior probability is close to 1, the alignment of this position
is highly reliable, whereas a posterior probability close to 0
identifies ambiguous positions. To assess confidence for positions
of multiple sequence alignments, a weighted sum of pairs scheme to
sum up the posterior probability of all pairs in the column is
calculated (Wu et al. 2012). All
alignment positions with a confidence score under a certain
threshold (e.g. >0.95) are excluded. GUIDANCE is a method where
alignment uncertainty is calculated by comparing alignment
positions across bootstrapped guide trees (Penn et al.
2010a; Penn et al. 2010b). This is based on the idea that the guide
tree, which is used by progressive alignment methods (see above),
introduces uncertainty. For example, different guide trees will
lead to different multiple sequence alignments. By using a simple
bootstrapping approach, multiple guide trees are generated and used
for alignment. Finally, the occurrence of every single position of
the original alignment is inspected in the alignments from the
perturbated trees. As more often a position occurs in the
alternative alignments, it is regarded to be more reliable.
According to a user-defined value, unreliable positions are
discarded. Alignments seem to be especially unreliable for sequence
regions containing many gaps. In an updated version called
GUIDANCE2, different gap opening costs are used to create further
alternative alignments which are inspected regarding consistency of
every single alignment position (Sela et al. 2015). Simulation studies comparing the here
described alignment maskers show that all of them improve the
accuracy of subsequent phylogenetic analyses based on the masked
alignment. Based on the analysed datasets, ZORRO and GUIDANCE
outperform ALISCORE and GBLOCKS, resulting in more significant
improvements of the alignment quality (Wu et al. 2012). This might be due to the fact that both
ZORRO and GUIDANCE calculate scores for every single position,
whereas «blocks» or «windows» of ambiguously aligned positions are
identified by ALISCORE and GBLOCKS. Finally, GUIDANCE2 seem to
outperform all here discussed methods (Sela et al. 2015).
6.5 Mapping Sequence Reads
A specific alignment application is
the mapping of sequence reads to already known reference sequences
(e.g. genomes, transcripts). Mapping is widely used to study gene
expression, DNA-protein interaction, RNA splicing, SNP detection,
or genome resequencing (Li et al. 2009b; Mortazavi et al. 2008; Nagalakshmi et al. 2008). Furthermore, mapping of sequence reads
has been successfully used for the discovery and genotyping of
transposable elements (Ewing 2015). The typical problem of read mapping is to
resolve the exact origin (location) of a sequence read in a given
reference sequence. This problem is complicated due to the
occurrence of repetitive sequences (and thereby several equally
likely locations), sequencing errors and genetic variation. Even
more challenging is the mapping of mRNA transcripts onto reference
genomes for the discovery of introns and splice variants, as huge
gaps are expected separating the ends of the sequencing read. The
BLAST algorithm described above could basically be used for read
mapping, but as the output of next-generation sequencing
technologies literally produce billions of short reads, more
efficient and less time- and memory-consuming methods have to be
explored. Nowadays several read mappers are available that are able
to map millions of sequence reads onto large genomes within
reasonable time using standard desktop computer resources.
Most mapping algorithms are either
based on a seed-and-extend approach (hash table indexing) or are
using methods based on the Burrows-Wheeler transform and specific
indexing forms (Li and Homer 2010). The seed-and-extend approach is basically
the same algorithm as used for BLAST searches. These approaches
trace the position of each k-mer (or word) of a predefined length
(e.g. 11 bps) of a query sequence and store them in a so-called
hash table. By referring to the hash table, the reference sequence
is scanned for exact matches of these k-mers, which are called seed, which
are then attempted to be elongated (► see 6.2). Retrieving all
k-mers of a sequence and
storing them in a table is called indexing. Several modified
versions of this approach enhancing speed and sensitivity are
implemented in read mapping software. For example, the software MAQ
uses spaced speed indexing, where every read is divided into four
segments which are used as seeds (Li et al. 2008a). By aligning all possible pairs of seeds
against the reference sequence the list of possible locations where
the full read maps can be limited quickly. The sensitivity of the
mapping can be controlled by defining the number of possible
mismatches of the seeds (spaced seeds). Other programs applying
this strategy are indexing the reference sequence instead of the
sequence reads, e.g. as implemented in SOAP (Li et al.
2008b) or BFAST (Homer et al.
2009). BFAST is first indexing the
reference sequence, and in a second step, all candidate alignment
locations are identified by using the stored k-mers. In a last step, a local
alignment allowing gaps is performed. However, seed-and-extend
approaches are intensive in the use of memory and computational
time.
Much more memory-efficient and less
time-consuming approaches of read mapping use an indexing scheme of
the reference sequence based on Burrows-Wheeler transform (BWT) and
FM-index (Ferragina and Manzini 2001), as, for example, implemented in the
software BOWTIE (Langmead et al. 2009; Langmead and Salzberg 2012) and BWA (Li and Durbin 2009). BWT has been initially developed for data
compression, e.g. to create zip files (Burrows and Wheeler
1994). Using BWT, a character
string (in our case a sequence) is transformed by sorting all
permutations of the string into lexical order and using the last
column of this table as output (◘ Fig. 6.10). Due to the lexical
ordering, transformed outputs will possess many repeated
characters, which make them easily compressible. Without any extra
information, it is possible to reverse the transformation of this
output into the original string (sequence) (◘ Fig. 6.11).



Fig.
6.10
Burrows-Wheeler transform of the string
>BONOBO*. The original sequence is permutated in all possible
orders, the rows are alphabetically ordered and last column is used
as output. > denotes the beginning of the sequence, * denotes
the end

Fig.
6.11
Inverse transformation of the output from
◘ Fig. 6.10
using Burrows-Wheeler transform. Starting with the output column,
columns are added and lexically ordered. These steps are cyclically
repeated till the original size of the string is recovered. The row
with the symbol (*) denoting the sequence end at its end represents
the original sequence (shaded)
The FM-index is a compressed
suffix-array-like index based on BWT. It was created as a data
structure that allows to locate and find a pattern within
compressed text (Ferragina and Manzini 2000). To create the FM-index, the lexically
sorted BWT of the sequence data is used. The transformed matrix can
be used for so-called last first (LF) mapping. This means the
ith occurrence of a character in the last column
corresponds to the ith occurrence of the same character
in the first column (Langmead et al. 2009). Using this lookup, exact matches of a
read in the reference can be traced by subsequently tracing
(aligning) the position of successively growing suffixes of the
read starting from its end. For example, a read AGCT would be
located along the rows of the BWT matrix in the order T, CT, GCT
and AGCT (Trapnell and Salzberg 2009). Whereas exact matches are working well to
find occurrences of words in a compressed book, it might be
problematical to locate sequence reads, as they may not match
exactly due to genetic variation or sequencing errors.
Consequently, an algorithm implementing so-called backtracking is
used to find inexact matches. This search is similar to that for
exact matches and calculates matrix locations (ranges of possible
rows) for successively longer suffixes of the query read. However,
in case a suffix is not found in the text, an already matched
suffix position is chosen and a substitution of a different base is
introduced, thereby allowing a mismatch in the alignment (Langmead
et al. 2009). Using a BWT approach
for mapping has some key advantages. First, BWT approaches are
memory efficient. The index for the complete human genome can be
stored into less than 2 Gb of RAM memory (usually available for
desktop computers), whereas by using a spaced seed approach, more
than 50 Gb RAM is needed (access to a high-performance computer
cluster necessary) (Trapnell and Salzberg 2009). Second, BWT approaches are also more time
efficient. For example, the BWT-based BOWTIE runs around 30 times
faster than MAQ, which uses a seed-and-extend approach.
Alternatively, alignment-free
approaches are available for read mapping, e.g. as implemented in
the software KALLISTO (Bray et al. 2016). In this case only the target sequence
where a read is originating from is stored – but not the exact
alignment position. In a first step, a de Bruijn graph of the
reference sequences (e.g. transcriptome data) is created as index,
where the nodes represent k-mers. Then, intersecting sets of
k-mer matches of the reads
are searched for in the graph to create pseudoalignments of the
reads. By doing this, the information of the order of all
k-mers of each single read
remains intact. A similar approach described as «lightweight
alignment» is used by the software SALMON (Patro et al.
2016). The advantage of these
approaches is that they are order of magnitudes faster than
alignment-based read mapping software, while being as accurate.
Both methods are especially useful for RNA-Seq quantification,
where only the information how many reads map on a specific
transcript is important, but not its exact position.
Fonseca et al. (2012) counted more than 60 available read
mappers in their review and even more have been published since
then. These programs differ not only in the underlying algorithms,
speed or memory efficiency but also in the ability to perform
specific mapping problems. As such it is possible to map DNA on
DNA, RNA on DNA or microRNAs back to the genome. For the detection
of methylation patterns, it is possible to map reads from
sequencing of bisulphite-treated DNA, where unmethylated C’s are
converted to T’s (Chen et al. 2010). Another typical read mapping problem is
the detection of splice junctions by mapping RNA-Seq reads onto a
reference genome. A commonly used pipeline for this application is
TOPHAT (Trapnell et al. 2009),
which combines two of the above discussed methods. First, all reads
are mapped onto the genome using BOWTIE. All reads that
successfully map are used to generate consensus assemblies of
possible exons, whereas reads which do not map onto the genome are
collected for a second step. The exact limits of the identified
exon regions are further refined based on the knowledge that most
introns of eukaryotic genes begin with GT (splice donor) and end
with AG (splice acceptor) (Mount 1982). Less frequent splice donor and acceptor
pairs are also recognized, e.g. GC-AG and AT-AC introns. Identified
exons represent possible splice sites. In a second step, the
remaining reads are mapped onto these splice site candidates by a
seed-and-extend approach using MAQ to find possible splices.
Recently, with HISAT (Kim et al. 2015), a replacement of TOPHAT has been
published. However, RNAs which are products of gene fusion,
circularization or trans-splicing are difficult to detect with this
approach. The read mapping software SEGEMEHL uses specific
algorithms to find these more unusual RNAs (Hoffmann et al.
2014). Several read mappers for
RNA-Seq data have been published, and their performance was
evaluated by Engström et al. (2013).
The output of read mapping is usually
stored in SAM- or BAM-format. The SAM-format consists of two
sections: a header section and an alignment section. Every line of
the header section starts with the character «@», whereas lines in
the alignment section do not have this characteristic (Li et al.
2009a). The SAM-format can store
plenty of information, e.g. quality scores, parameters of the used
software, etc. (◘ Fig. 6.12). The BAM-format is the binary equivalent
of the SAM-format, making it more compressed and less memory
intensive. BAM-files are not only used to store alignment
information but also in the submission of raw-sequencing data to
NCBI GenBank. Conversion of SAM-files to BAM-files and vice versa
can be conducted by SAM-TOOLS (Li et al. 2009a). As SAM/BAM-files contain sequence and
quality data, they can be easily converted into FASTQ- or
FASTA-format, which are widely used formats for assembly or
multiple sequence alignments.


Fig.
6.12
Example of the SAM-format. The first four
rows comprise the header section (HEADER) in this case including a
header line (@HD), a reference sequence dictionary (@SD) and
information about the used program (@PG). The next rows are the
alignment section, always starting with the name of the read to map
(QNAME), followed by the FLAG containing information about the
sequence read. RNAME denotes the name of the reference sequence and
the first position where the read starts to align in the reference
(POS). The quality of the mapping can be indicated (MAPQ), and the
CIGAR describes how the read maps. For example, 97M1D3M means that
the first 97 bases are matching the reference, 1D describes a
deletion in the reference, and the last 3 bases of the read match
again. RNEXT gives information about the next mapping read (e.g.
reverse read) and its starting position (PNEXT), TLEN describes the
length of the template (e.g. read pair). This is followed by a
string of characters which represent the actual mapped sequence
(SEQ) and a string with its according quality values (QUAL).
Additional information can be given as optional tags
6.6 Whole-Genome Alignments
For many comparative genomic analyses,
it is necessary to align complete genomes. By comparing two
genomes, differences can be found locally, but also at large scale
(Darling et al. 2010; Feuk et al.
2006). For example, at local
scales mutations will occur between two compared genome sequences,
but also insertions and deletions. These are basically the same
processes that have to be resolved as in alignments of sequences.
However, at the genome level, also large-scale changes have to be
taken into account, as genes or genomic regions can be either
gained or lost. Some regions will be completely missing, whereas
for duplicated regions, homology has to be inferred. Moreover, the
order of genes or genomic regions can be massively rearranged.
Local mutations do not change the order of sequence positions and
can be inferred by collinear alignment methods as introduced in
this chapter. In contrast, large-scale changes can lead to
noncollinear changes and need to be addressed by alignment
approaches that focus on many different kinds of evolutionary
changes of the genome. Whereas in collinear alignments, positional
homology is inferred, the detection of noncollineary changes is
basically the prediction of orthology of genes or larger genomic
regions (Dewey 2012; Dewey and
Pachter 2006).
Most whole-genome alignment methods
can be broadly classified into hierarchical and local approaches
(Dewey 2012). Using the
hierarchical approach, collinear and homologous (ideally
orthologous) segments are identified first. In a second step,
global sequence alignments on a nucleotide level of these collinear
segments are conducted. A widely used software implementing such an
approach is progressiveMAUVE (Darling et al. 2010). Local approaches firstly conduct large
sets of nucleotide alignments of genomic regions, which in
subsequent steps are filtered and merged to produce alignments of
homologous (ideally orthologous) genomic regions. MUMMER (Delcher
et al. 1999) is among the most
frequently used software solutions based on this approach.
Preservation of the order of genes or
genomic regions along the chromosomes is called synteny (Bentley
and Parkhill 2004). By conducting
whole-genome alignments, syntenic regions across compared genomes
can be identified and visualized. Synteny is used to identify
conserved regions across compared genomes which are often
interpreted as functional regions. Synteny of large regions of
vertebrate genomes was already noticed in the pre-genomic era of
molecular biology and interpreted as «frozen accidents» (Ohno
1973). It was first assumed that
chromosomal rearrangements, which are able to break up larger
syntenic regions, are randomly distributed within the genome of
eukaryotes (Nadeau and Taylor 1984). Based on this idea, syntenic regions are
basically relicts in the eukaryote genome (Kikuta et al.
2007). However, the increasing
availability of completely sequenced genomes led to the discovery
of syntenic blocks across deeply diverged lineages, which clearly
suggest evolutionary conservation of these genomic regions.
Earliest known examples are represented by clustering of Hox-genes
among most investigated Metazoa (Ferrier and Holland 2001). However, as this gene family arose by
tandem duplication, it might be an exception. Interestingly,
large-scale genomic studies revealed that co-expressed genes are
statistically more often clustered within the genome than expected,
which has been demonstrated for all major eukaryotic lineages
(Hurst et al. 2004). Furthermore,
large genomic regulatory blocks including developmental regulatory
genes and highly conserved non-coding sequences have been
identified in vertebrate and insect genomes (Kikuta et al.
2007; Engström et al.
2007). Synteny is even more
pronounced across bacterial and archaeal genomes, where
co-expressed genes under the control of the same promoter are
organized in operons.
References
Altschul SF, Madden TL,
Schäffer AA, Zhang J, Zhang Z, Miller W, Lipman DJ (1997) Gapped
BLAST and PSI-BLAST: a new generation of protein database search
programs. Nucleic Acids Res 25:3389–3402CrossRefPubMedPubMedCentral
Bradley RK, Roberts A, Smoot
M, Juvekar S, Do J, Dewey C, Holmes I, Pachter L (2009) Fast
statistical alignment. PLoS Comput Biol 5:e1000392CrossRefPubMedPubMedCentral
Burrows M, Wheeler DJ (1994)
A block-sorting lossless data compression algorithm. Digital
Equipment Corporation Technical Report 124, Palo Alto
Chen P-Y, Cokus SJ,
Pellegrini M (2010) BS seeker: precise mapping for bisulfite
sequencing. BMC Bioinformatics 11:203CrossRefPubMedPubMedCentral
Cooper L, Cooper MW (1981)
Introduction to dynamic programming. Pergamon Press, New York
Cristianini N, Hahn MW
(2007) Introduction to computational genomics. Cambridge University
Press, Cambridge, UK, A case studies approach
Darling AE, Mau B, Perna NT
(2010) progressiveMauve: multiple genome alignment with gene gain,
loss and rearrangement. PLoS One 5:e11147CrossRefPubMedPubMedCentral
Delcher AL, Kasif S,
Fleischmann RD, Peterson J, White O, Salzberg SL (1999) Alignment
of whole genomes. Nucleic Acids Res 27:2369–2376CrossRefPubMedPubMedCentral
Dewey CN (2012) Whole-genome
alignment. In: Anisimova M (ed) Evolutionary genomics: statistical
and computational methods, vol 1. Humana Press, Totowa, pp
237–257
Edgar RC (2004) MUSCLE: a
multiple sequence alignment method with reduced time and space
complexity. BMC Bioinformatics 5:1–19CrossRef
Engström PG, Ho Sui SJ,
Drivenes Ø, Becker TS, Lenhard B (2007) Genomic regulatory blocks
underlie extensive microsynteny conservation in insects. Genome Res
17:1898–1908CrossRefPubMedPubMedCentral
Engström PG, Steijger T,
Sipos B, Grant GR, Kahles A, The RC, Ratsch G, Goldman N, Hubbard
TJ, Harrow J, Guigo R, Bertone P (2013) Systematic evaluation of
spliced alignment programs for RNA-seq data. Nat Methods
10:1185–1191CrossRefPubMedPubMedCentral
Ewing AD (2015) Transposable
element detection from whole genome sequence data. Mob DNA
6:24CrossRefPubMedPubMedCentral
Ferragina P, Manzini G
(2000) Opportunistic data structures with applications. In: 41st
annual symposium on Foundations of Computer Science, Washington,
DC
Ferragina P, Manzini G
(2001) An experimental study of an opportunistic index. Paper
presented at the proceedings of the twelfth annual ACM-SIAM
symposium on Discrete Algorithms, Washington, DC
Gardner PP, Wilm A, Washietl
S (2005) A benchmark of multiple sequence alignment programs upon
structural RNAs. Nucleic Acids Res 33:2433–2439CrossRefPubMedPubMedCentral
Henikoff S, Henikoff JG
(1992) Amino acid substitution matrices from protein blocks. Proc
Natl Acad Sci U S A 89:10915–10919CrossRefPubMedPubMedCentral
Hoffmann S, Otto C, Doose G,
Tanzer A, Langenberger D, Christ S, Kunz M, Holdt L, Teupser D,
Hackermuller J, Stadler P (2014) A multi-split mapping algorithm
for circular RNA, splicing, trans-splicing and fusion detection.
Genome Biol 15:R34CrossRefPubMedPubMedCentral
Homer N, Merriman B, Nelson
SF (2009) BFAST: an alignment tool for large scale genome
resequencing. PLoS One 4:e7767CrossRefPubMedPubMedCentral
Katoh K, Standley DM (2013)
MAFFT multiple sequence alignment software version 7: improvements
in performance and usability. Mol Biol Evol 30:772–780CrossRefPubMedPubMedCentral
Kent WJ (2002) BLAT—the
BLAST-like alignment tool. Genome Res 12:656–664CrossRefPubMedPubMedCentral
Kikuta H, Laplante M,
Navratilova P, Komisarczuk AZ, Engström PG, Fredman D, Akalin A,
Caccamo M, Sealy I, Howe K, Ghislain J, Pezeron G, Mourrain P,
Ellingsen S, Oates AC, Thisse C, Thisse B, Foucher I, Adolf B,
Geling A, Lenhard B, Becker TS (2007) Genomic regulatory blocks
encompass multiple neighboring genes and maintain conserved synteny
in vertebrates. Genome Res 17:545–555CrossRefPubMedPubMedCentral
Kim D, Langmead B, Salzberg
SL (2015) HISAT: a fast spliced aligner with low memory
requirements. Nat Methods 12:357–360CrossRefPubMedPubMedCentral
Kück P, Meusemann K, Dambach
J, Thormann B, von Reumont BM, Wägele JW, Misof B (2010) Parametric
and non-parametric masking of randomness in sequence alignments can
be improved and leads to better resolved trees. Front Zool
7:10CrossRefPubMedPubMedCentral
Langmead B, Salzberg SL
(2012) Fast gapped-read alignment with bowtie 2. Nat Methods
9:357–359CrossRefPubMedPubMedCentral
Langmead B, Trapnell C, Pop
M, Salzberg S (2009) Ultrafast and memory-efficient alignment of
short DNA sequences to the human genome. Genome Biol
10:R25CrossRefPubMedPubMedCentral
Lassmann T, Sonnhammer ELL
(2005) Automatic assessment of alignment quality. Nucleic Acids Res
33:7120–7128CrossRefPubMedPubMedCentral
Levinson G, Gutman GA (1987)
Slipped-strand mispairing: a major mechanism for DNA sequence
evolution. Mol Biol Evol 4:203–221PubMed
Li H, Durbin R (2009) Fast
and accurate short read alignment with burrows-wheeler transform.
Bioinformatics 25:1754–1760CrossRefPubMedPubMedCentral
Li H, Homer N (2010) A
survey of sequence alignment algorithms for next-generation
sequencing. Brief Bioinform 11:473–483CrossRefPubMedPubMedCentral
Li H, Ruan J, Durbin R
(2008a) Mapping short DNA sequencing reads and calling variants
using mapping quality scores. Genome Res 18:1851–1858CrossRefPubMedPubMedCentral
Li H, Handsaker B, Wysoker
A, Fennell T, Ruan J, Homer N, Marth G, Abecasis G, Durbin R,
Subgroup GPDP (2009a) The Sequence Alignment/Map format and
SAMtools. Bioinformatics 25:2078–2079CrossRefPubMedPubMedCentral
Li R, Li Y, Fang X, Yang H,
Wang J, Kristiansen K, Wang J (2009b) SNP detection for massively
parallel whole-genome resequencing. Genome Res
19:1124–1132CrossRefPubMedPubMedCentral
McGuffin L (2009) Insertion
and deletion events, their molecular mechanisms, and their impact
on sequence alignments. In: Rosenberg M (ed) Sequence alignment:
methods, models, concepts and strategies. Universtiy of California
Press, Berkeley, pp 23–38
Morgenstern B (2009) Local
versus global alignments. In: Rosenberg M (ed) Sequence alignment:
methods, models, concepts and strategies. Universtiy of California
Press, Berkeley, pp 39–53
Mount SM (1982) A catalogue
of splice junction sequences. Nucleic Acids Res
10:459–472CrossRefPubMedPubMedCentral
Nadeau JH, Taylor BA (1984)
Lengths of chromosomal segments conserved since divergence of man
and mouse. Proc Natl Acad Sci U S A 81:814–818CrossRefPubMedPubMedCentral
Nagalakshmi U, Wang Z, Waern
K, Shou C, Raha D, Gerstein M, Snyder M (2008) The transcriptional
landscape of the yeast genome defined by RNA sequencing. Science
320:1344–1349CrossRefPubMedPubMedCentral
Ohno S (1973) Ancient
linkage groups and frozen accidents. Nature 244:259–262CrossRef
Patro R, Duggal G, Love MI,
Irizarry RA, Kingsford C (2016) Salmon provides accurate, fast, and
bias-aware transcript expression estimates using dual-phase
inference. bioRxiv. doi.org/10.1101/021592.
Penn O, Privman E, Ashkenazy
H, Landan G, Graur D, Pupko T (2010a) GUIDANCE: a web server for
assessing alignment confidence scores. Nucleic Acids Res
38:W23–W28CrossRefPubMedPubMedCentral
Penn O, Privman E, Landan G,
Graur D, Pupko T (2010b) An alignment confidence score capturing
robustness to guide tree uncertainty. Mol Biol Evol
27:1759–1767CrossRefPubMedPubMedCentral
Pevsner J (2015)
Bioinformatics and functional genomics, 3rd edn. Wiley-Blackwell,
Hoboken
Rosenberg M (2009) Sequence
alignment: concepts and history. In: Rosenberg M (ed) Sequence
alignment: methods, models, concepts and strategies. Universtiy of
California Press, Berkeley, pp 1–22
Sela I, Ashkenazy H, Katoh
K, Pupko T (2015) GUIDANCE2: accurate detection of unreliable
alignment regions accounting for the uncertainty of multiple
parameters. Nucleic Acids Res 43:W7–W14CrossRefPubMedPubMedCentral
Thompson JD, Higgins DG,
Gibson TJ (1994) CLUSTAL W: improving the sensitivity of
progressive multiple sequence alignment through sequence weighting,
position-specific gap penalties and weight matrix choice. Nucleic
Acids Res 22:4673–4680CrossRefPubMedPubMedCentral
Thompson JD, Koehl P, Ripp
R, Poch O (2005) BAliBASE 3.0: latest developments of the multiple
sequence alignment benchmark. Proteins: Structure, Function, and
Bioinformatics 61:127–136CrossRef
Thompson JD, Linard B,
Lecompte O, Poch O (2011) A comprehensive benchmark study of
multiple sequence alignment methods: current challenges and future
perspectives. PLoS One 6:e18093CrossRefPubMedPubMedCentral
Thorne JL, Kishino H (1992)
Freeing phylogenies from artifacts of alignment. Mol Biol Evol
9:1148–1162PubMed
Trapnell C, Salzberg SL
(2009) How to map billions of short reads onto genomes. Nat
Biotechnol 27:455–457CrossRefPubMedPubMedCentral
Trapnell C, Pachter L,
Salzberg SL (2009) TopHat: discovering splice junctions with
RNA-seq. Bioinformatics 25:1105–1111CrossRefPubMedPubMedCentral
Wu M, Chatterji S, Eisen JA
(2012) Accounting for alignment uncertainty in phylogenomics. PLoS
One 7:e30288CrossRefPubMedPubMedCentral