10
L’UNIFICATION DE LA PHYSIQUE
Comme je l’ai expliqué dans le premier chapitre, il serait très difficile de construire une théorie complètement unifiée valable pour tout dans l’univers. Mais à la place, nous avons fait des progrès en trouvant des théories partielles qui décrivent un enchaînement limité d’événements en négligeant d’autres effets ou en les approchant par certains nombres. (La chimie, par exemple, nous permet de calculer les interactions entre atomes sans rien connaître de la structure interne du noyau d’un atome.) En fin de compte, cependant, on peut espérer trouver une théorie complète, logique et unifiée, qui inclurait toutes ces théories partielles en tant qu’approximations et qu’il ne serait pas nécessaire d’adapter pour encadrer les faits en choisissant les valeurs de certains nombres arbitraires dans la théorie. La quête d’une telle théorie est connue aujourd’hui sous la dénomination d’« unification de la physique ». Einstein a passé sans succès le plus clair de ses dernières années à la recherche d’une théorie unifiée mais l’heure de celle-ci n’avait pas encore sonné : il y avait des théories partielles pour la gravitation et pour la force électromagnétique mais on ne savait que peu de chose sur les forces nucléaires. De plus, Einstein refusait de croire à la réalité de la mécanique quantique, en dépit du rôle important qu’il avait joué dans son développement. Cependant, le principe d’incertitude est une caractéristique fondamentale de l’univers dans lequel nous vivons. Une théorie unifiée valable doit nécessairement en tenir compte.
Comme je le décrirai par la suite, les perspectives de trouver une telle théorie semblent être bien meilleures aujourd’hui parce que nous en savons beaucoup plus sur l’univers. Mais nous devons nous garder de toute présomption – nous avons connu d’autres espoirs fallacieux auparavant ! Au début de ce siècle, par exemple, on pensait que tout pourrait être expliqué en termes de propriétés de la matière continue, comme l’élasticité ou la conduction calorifique. La découverte de la structure atomique et le principe d’incertitude mirent un point final à tout cela. Puis, en 1928, le prix Nobel de physique Max Born annonça à un groupe de visiteurs à l’université de Göttingen que « la physique, comme on le sait, sera terminée dans six mois ». Sa confiance se fondait sur la découverte récente faite par Dirac de l’équation qui gouvernait l’électron. On pensait qu’une équation similaire pourrait gouverner le proton, seule particule connue à l’époque, et que ce serait la fin de la physique théorique. La découverte du neutron et des forces nucléaires rabattit à nouveau cette belle confiance. Ayant dit cela, je crois encore qu’il y a quand même des bases d’optimisme prudent qui nous permettent d’espérer la fin prochaine de la quête des lois ultimes de la nature.
Dans les chapitres précédents, j’ai décrit la Relativité Générale, théorie partielle de la gravitation, et les théories partielles qui commandent aux forces électromagnétique, forte et faible. Les trois dernières peuvent être combinées dans ce que l’on appelle les théories de la grande unification, ou GUT, qui ne sont pas vraiment satisfaisantes parce qu’elles n’incluent pas la gravitation et parce qu’elles contiennent un certain nombre de quantités, comme les masses relatives de différentes particules, qui ne peuvent être prédites par la théorie mais qui doivent être choisies pour cadrer avec les observations. La principale difficulté pour trouver une théorie qui unifie la gravitation avec les autres forces est que la Relativité Générale est une théorie « classique », c’est-à-dire qu’elle ne contient pas le principe d’incertitude de la mécanique quantique. Par ailleurs, les théories partielles dépendent essentiellement de la mécanique quantique. Un premier pas nécessaire sera donc de combiner la Relativité Générale avec le principe d’incertitude. Comme nous l’avons vu, cela peut amener de remarquables conséquences, telles que les trous noirs qui ne sont pas noirs, ou l’univers sans singularité et sans bord. L’ennui c’est que, comme nous l’avons expliqué au chapitre 7, le principe d’incertitude signifie que même « vide », l’espace est rempli de paires de particules virtuelles et d’antiparticules. Ces paires devraient avoir une quantité infinie d’énergie et donc, par la célèbre équation d’Einstein E = mc², elles devraient avoir une masse infinie. Leur attraction gravitationnelle devrait alors courber l’univers jusqu’à une dimension infiniment petite.
Dans le même genre, des infinis absurdes à première vue interviennent dans les autres théories partielles, mais dans tous les cas ces infinis peuvent être annulés par un procédé appelé « renormalisation ». Bien que cette technique soit relativement douteuse sur le plan mathématique, elle semble marcher en pratique et elle a été appliquée à ces théories pour faire des prédictions qui collent aux observations avec un extraordinaire degré de précision. La renormalisation, cependant, a un sérieux inconvénient du point de vue de la recherche d’une théorie complète, parce que cela signifie que les valeurs réelles des masses et les intensités des forces ne peuvent être prédites par la théorie mais doivent être choisies de manière à coller aux observations.
En essayant d’incorporer le principe d’incertitude dans la Relativité Générale, on n’a que deux quantités à ajuster : l’intensité de la gravité et la valeur de la constante cosmologique. Mais les ajuster n’est pas suffisant pour ôter tous les infinis. On a donc une théorie qui semble prédire que certaines quantités, comme la courbure de l’espace-temps, sont réellement infinies, alors que ces mêmes quantités peuvent être observées et mesurées comme parfaitement finies ! Ce problème de combinaison de la Relativité Générale et du principe d’incertitude a été suspecté pendant un certain temps mais a finalement été confirmé par des calculs détaillés en 1972. Quatre ans plus tard, une solution possible, appelée « supergravité », a été proposée. Cette notion combinait une particule de spin 2 appelée graviton, qui sert de support à la force gravitationnelle, avec certaines autres nouvelles particules de spin 3/2, 1, 1/2 et 0. En un sens, toutes ces particules pouvaient être considérées comme des aspects différents de la même « superparticule », donc unifiant les particules de matière de spin 1/2 et 3/2 avec les particules supports-de-force de spin 0, 1 et 2. Les paires virtuelles de particules/anti-particules de spin 1/2 et 3/2 auraient une énergie négative et donc tendraient à annuler l’énergie positive des paires virtuelles de spin 2, 1 et 0. Cela serait la cause de beaucoup d’infinis possibles à annuler, mais on pensait que quelques infinis subsisteraient toujours. Cependant, les calculs qui permettraient de savoir s’il resterait des infinis ou non étaient si longs et si difficiles que personne n’était prêt à s’y engager. Même avec un ordinateur, on a calculé que cela prendrait au moins quatre ans et que les occasions seraient très grandes que l’on commette au moins une faute, si ce n’est plus. Et l’on sait que l’on n’aura la bonne réponse que si quelqu’un d’autre refait les calculs et arrive au même résultat, mais il n’y a pas grande chance que cela arrive !
En dépit de ces problèmes, et du fait que les particules dans les théories de supergravité ne semblaient pas se comporter comme les particules observées, la plupart des scientifiques pensaient que la supergravité était probablement la bonne réponse au problème de l’unification de la physique. Cela semblerait être le meilleur moyen d’unifier gravité et autres forces. Cependant, en 1984, il y eut un remarquable mouvement d’opinion en faveur de ce que l’on a appelé les « théories des cordes ». Dans ces théories, les objets de base ne sont pas des particules qui occupent un seul point dans l’espace, mais des entités qui ont une longueur mais pas d’autres dimensions, comme un morceau de corde infiniment mince. Ces cordes peuvent avoir des bouts (ce sont les cordes ouvertes) ou elles peuvent se refermer sur elles-mêmes en boucles fermées (cordes fermées) (fig. 10.1 et fig. 10.2). Une particule occupe un point de l’espace à chaque instant du temps ; aussi son chemin dans l’espace-temps est-il une ligne (sa « ligne d’univers »). Une corde, au contraire, occupe à chaque instant une ligne dans l’espace. Aussi sa trace dans l’espace-temps est-elle une surface bidimensionnelle appelée « feuille d’univers ». (Chaque point d’une telle feuille d’univers peut être décrit par deux nombres : l’un spécifiant le temps, et l’autre, la position du point sur la corde). La feuille d’univers d’une corde ouverte est une bande ; ses bords représentent les trajectoires dans l’espace-temps des bouts de la corde (fig. 10.1). La feuille d’univers d’une corde fermée est un cylindre ou un tube (fig. 10.2) ; une section du tube est un cercle, représentant la position d’une corde à un instant donné.
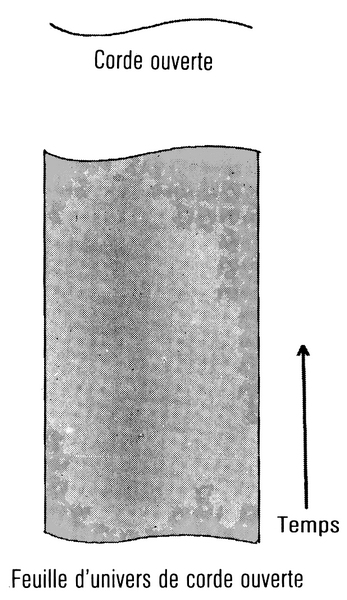
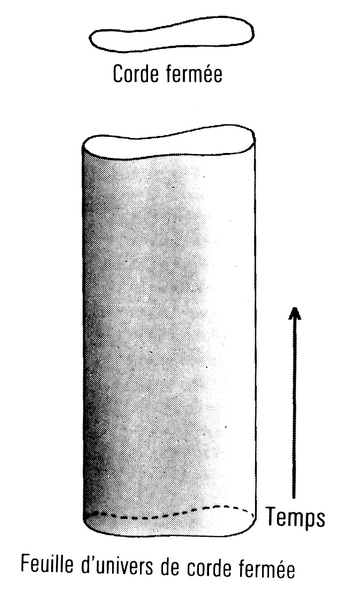
Figure 10.1 et 10.2
Deux morceaux de cordes peuvent s’ajouter pour former une seule corde ; dans le cas de cordes ouvertes, elles se joignent simplement à leurs bouts (fig. 10.3), alors que dans le cas de cordes fermées, c’est comme les deux jambes d’un pantalon (fig. 10.4). De même, un morceau de corde peut se diviser en deux cordes.
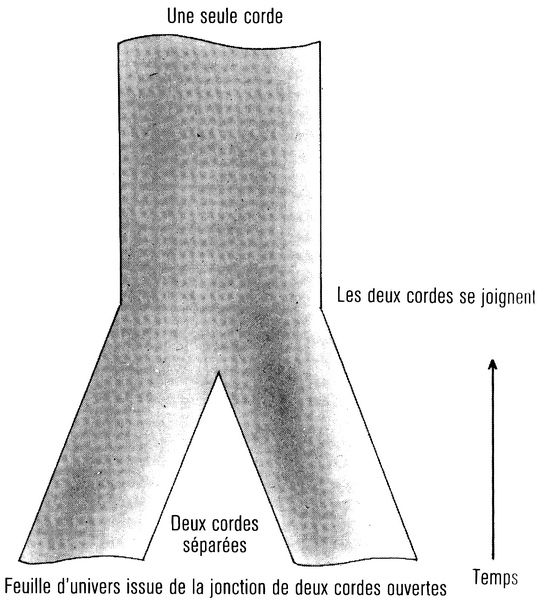
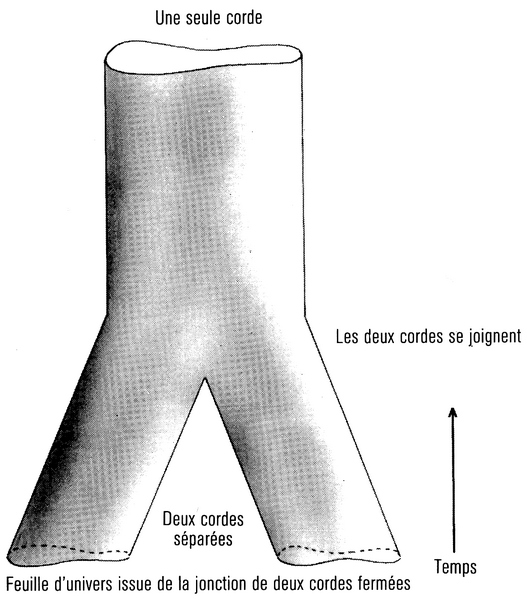
Dans les théories des cordes, ce que l’on pensait auparavant en termes de particules est maintenant représenté comme des ondes voyageant le long d’une corde, comme les ondes d’une corde de cerf-volant en vibration. L’émission ou l’absorption d’une particule par une autre correspond à la division ou à la jonction de cordes. Par exemple, la force gravitationnelle du Soleil sur la Terre est représentée, en théorie des particules, par l’émission d’un graviton par le Soleil et son absorption par une particule de la Terre (fig. 10.5). Dans la théorie des cordes, ce procédé correspond à un tube en forme de H (fig. 10.6) (la théorie des cordes est un peu comme de la plomberie, en quelque sorte). Les deux jambes du H correspondent aux particules du Soleil et de la Terre et la barre horizontale correspond au graviton qui voyage entre eux.
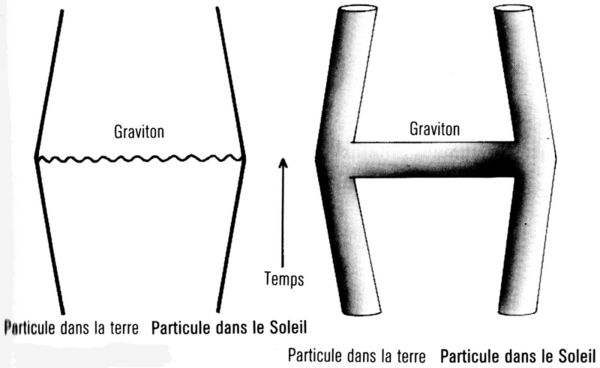
Figure 10.5 et 10.6
La théorie des cordes a une curieuse histoire. Elle fut inventée à la fin des années soixante dans l’intention de trouver une théorie qui décrive l’interaction forte. L’idée était que les particules comme le proton et le neutron pourraient être comparées à des ondes sur une corde. Les interactions fortes entre les particules correspondraient aux morceaux de corde qui joignent d’autres bouts de corde comme sur une toile d’araignée. Pour que cette théorie donne la valeur observée de l’interaction forte entre les particules, les cordes devaient être comme des élastiques supportant des tractions d’environ dix tonnes.
En 1974, Joël Scherk à Paris et John Schwarz au California Institute of Technology publièrent un article dans lequel ils montraient que la théorie des cordes décrivait la force gravitationnelle, mais seulement si la tension dans la corde était beaucoup plus grande, d’environ mille milliards de milliards de milliards de milliards de tonnes (un 1 avec 39 zéros derrière). Les prédictions de la théorie des cordes seraient exactement les mêmes que celles de la Relativité Générale, à des échelles de longueur normales, mais elles seraient différentes à de très petites distances, de moins d’un millionième de milliardième de milliardième de milliardième de centimètre (un centimètre divisé par 1 avec 33 zéros derrière). Leur travail ne fut pas très remarqué, cependant, parce que juste à ce moment, la plupart des gens abandonnèrent la théorie originale des cordes sur l’interaction forte en faveur d’une théorie basée sur les quarks et les gluons, qui semblait mieux correspondre aux observations. Scherk mourut dans de tragiques circonstances (il souffrait de diabète et entra dans le coma alors que personne ne se trouvait à proximité pour lui faire une injection d’insuline.) Aussi Schwarz resta-t-il seul pour soutenir la théorie des cordes mais maintenant, avec une valeur de tension beaucoup plus élevée.
En 1984, l’intérêt pour les cordes se réveilla soudain, pour deux raisons apparemment. L’une d’elles était que les gens ne faisaient pas vraiment de progrès pour montrer que la supergravité était vraie ou qu’elle expliquait les sortes de particules que nous observons. L’autre, ce fut la publication d’un article signé John Schwarz et Mike Green, du Queen Mary College à Londres, qui montrait que la théorie des cordes devait être capable d’expliquer l’existence de particules orientées à gauche, comme certaines des particules que nous observons.
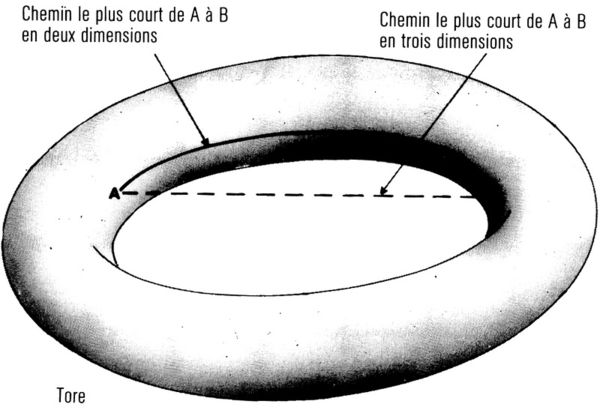
La théorie des cordes mène aussi à des infinis, mais l’on pense qu’ils seront annulés dans des versions comme celles des cordes dites « hétérotiques » (bien que cela ne soit pas encore certain). Les théories des cordes, cependant, rencontrent un gros problème : elles semblent n’être valables que si l’espace-temps a ou dix ou vingt-six dimensions au lieu de nos quatre habituelles ! Bien sûr, les dimensions supplémentaires d’espace-temps sont choses courantes en science-fiction ; même, elles sont presque une nécessité, alors qu’autrement le fait que la relativité implique qu’on ne peut voyager plus vite que la lumière signifie que cela demanderait trop de temps pour voyager entre les étoiles et les galaxies. L’idée de la science-fiction est que peut-être on pourrait prendre un raccourci par une autre dimension. On peut décrire cela de la façon suivante : imaginez que l’espace dans lequel nous vivons n’a que deux dimensions et est courbe comme la surface d’un anneau (fig. 10.7). Si vous êtes d’un côté du bord interne de l’anneau et que vous vouliez aller à un point de l’autre côté, vous devriez suivre le bord incurvé interne de l’anneau. Cependant, si vous pouvez voyager en trois dimensions, vous couperiez droit sur le point en face.
Pourquoi ne remarquons-nous pas toutes ces dimensions supplémentaires si elles existent réellement ? Pourquoi n’en voyons-nous que trois d’espace et une de temps ? On suppose que les autres dimensions sont courbes dans un espace de très petite taille, quelque chose comme le millième de milliardième de milliardième de milliardième de centimètre. C’est si petit que nous ne le remarquons tout simplement pas ; nous voyons seulement une dimension de temps et trois dimensions d’espace, dans lesquelles l’espace-temps est assez plat. C’est comme la surface d’une orange : si vous la regardez de près, elle est toute courbe et ridée, mais si vous la regardez de plus loin, vous ne verrez pas les inégalités et elle semblera lisse. Il en est de même pour l’espace-temps : à très petite échelle, il est à dix dimensions et très courbé, mais à plus grande échelle, vous ne voyez pas sa courbure ou ses dimensions supplémentaires. Si cette représentation est correcte, elle annonce de mauvaises nouvelles pour ceux qui voudraient voyager dans l’espace : les dimensions supplémentaires seraient par trop petites pour autoriser un voyage à travers elles. Cependant, cela soulève un autre problème majeur. Pourquoi est-ce que quelques-unes seulement des dimensions, et non toutes, sont enroulées comme à l’intérieur d’une balle ? On présume que dans l’univers très primitif, toutes les dimensions ont été ainsi très courbes. Pourquoi est-ce qu’une dimension de temps et trois dimensions d’espace se sont-elles « ouvertes », alors que les autres restaient fortement enroulées sur elles-mêmes ?
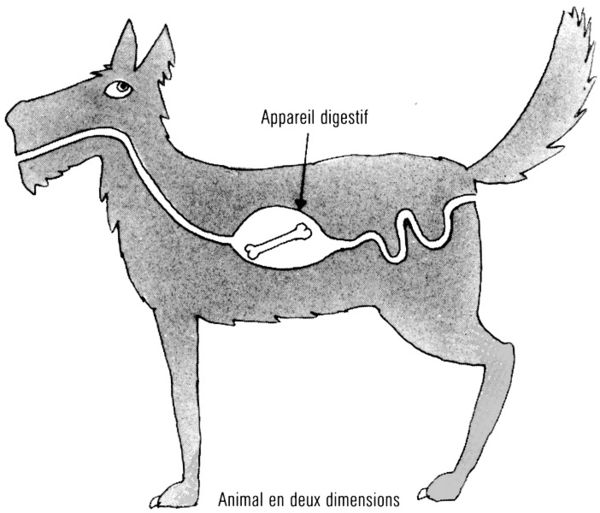
Une réponse possible est le principe anthropique. Deux dimensions dans l’espace ne semblent pas suffisantes pour permettre le développement d’êtres complexes comme nous. Par exemple, des animaux à deux dimensions vivant sur une Terre à deux dimensions devraient grimper l’un sur l’autre pour se dépasser. Si une créature à deux dimensions mangeait quelque chose qu’elle ne peut pas digérer complètement, elle devrait rendre les restes par le même chemin par lequel elle les a ingérés parce que s’il y avait eu un passage à travers son corps, cela aurait divisé la créature en deux moitiés séparées (fig. 10.8). De même, il est difficile de voir comment pourrait exister une quelconque circulation sanguine dans une créature à deux dimensions.
Il devrait aussi y avoir des problèmes avec plus de trois dimensions. La force gravitationnelle entre deux corps décroîtrait plus rapidement avec la distance qu’elle ne le fait en trois dimensions. (En trois dimensions, la force gravitationnelle tombe à 1 /4 si l’on va deux fois plus loin. En quatre dimensions, elle décroîtrait jusqu’à 1/8, en cinq dimensions, à 1/16, etc.). La signification de cela est que l’orbite des planètes, comme la Terre, autour du Soleil serait instable : la moindre perturbation sur une orbite circulaire (comme celle qui serait causée par l’attraction gravitationnelle des autres planètes) amènerait la Terre à spiraler loin ou vers le Soleil. Ou nous gèlerions ou nous serions carbonisés. En fait, le même comportement de la gravité avec la distance dans plus de trois dimensions de l’espace signifie que le Soleil ne serait pas capable d’exister dans un état stable avec la pression contrebalançant la gravité. Ou il se désagrégerait, ou il s’effondrerait en trou noir. Dans tous les cas, il ne serait pas de grande utilité en tant que source de chaleur et de lumière pour la vie sur Terre. À plus petite échelle, les forces électriques, qui font que les électrons tournent autour du noyau dans un atome, se comporteraient de la même façon que les forces gravitationnelles. Ainsi, les électrons pourraient s’échapper de l’atome ou spiraler jusqu’au noyau. Dans l’un ou l’autre cas, nous n’aurions pas d’atomes.
Il semble clair, alors, que la vie, telle que nous la connaissons, ne peut exister que dans les régions de l’espace-temps dans lesquelles une dimension de temps et trois dimensions d’espace ne sont pas fortement enroulées sur elles-mêmes. Cela signifie que l’on peut faire appel au principe anthropique pourvu que l’on puisse montrer que la théorie des cordes permet au moins qu’il y ait là de telles régions de l’univers – et il semble qu’elle le fasse effectivement. Il peut très bien y avoir d’autres régions de l’univers, ou d’autres univers (quoi que cela signifie), dans lesquels toutes les dimensions sont fortement enroulées ou dans lesquels plus de quatre dimensions sont près d’être plates, mais il ne pourrait pas y avoir d’êtres intelligents dans de telles régions pour observer les nombres différents de dimensions effectives.
Sans rapport avec la question du nombre de dimensions que l’espace-temps semble avoir, la théorie des cordes rencontre encore d’autres problèmes qui doivent être résolus avant qu’on la déclare théorie ultime d’unification de la physique. Nous ne savons pas encore si tous les infinis s’annuleront les uns les autres, ou comment exactement relier les ondes aux cordes pour des types particuliers de particules que nous observons. Néanmoins, il y a une chance que les réponses à ces questions apparaissent dans les quelques prochaines années et qu’avant la fin du siècle, nous sachions si la théorie des cordes est vraiment la théorie unifiée de la physique si longtemps recherchée.
Mais peut-il y avoir réellement une telle théorie ? Ou sommes-nous seulement en train de poursuivre un mirage ? Il semble qu’il y ait trois possibilités :
1) Il y a effectivement une théorie complètement unifiée, que nous découvrirons un jour si nous nous montrons assez malins pour cela.
2) Il n’y a pas de théorie ultime de l’univers, juste une suite infinie de théories qui décrivent l’univers plus ou moins précisément.
3) Il n’y a pas de théorie de l’univers ; les événements ne peuvent être prédits au-delà d’un certain point et arrivent au hasard et de manière arbitraire.
Certains soutiendront la troisième possibilité en se fondant sur le fait que s’il existait un ensemble complet de lois, cela enfreindrait la liberté de Dieu de changer d’avis et d’intervenir dans le monde. C’est un peu comme le vieux paradoxe : Dieu peut-il créer une pierre si lourde qu’il ne puisse la soulever ? Mais cette idée que Dieu puisse vouloir changer d’avis est un exemple de sophisme, remarqué par saint Augustin, d’imaginer Dieu comme un être existant dans le temps : le temps est seulement une propriété de l’univers que Dieu a créé. Il est probable qu’il savait ce qu’il voulait faire lorsqu’il le créa !
Avec l’avènement de la mécanique quantique, nous sommes amenés à reconnaître que les événements ne peuvent être prédits avec une complète exactitude et qu’il y a toujours un degré d’incertitude. Si l’on veut, on peut décrire ce hasard de l’intervention de Dieu, mais ce serait une très étrange sorte d’intervention : il n’y a aucune preuve qu’elle obéisse à un dessein. Si c’était vraiment le cas, ce ne serait pas du hasard, par définition. À l’époque moderne, nous avons effectivement effacé la troisième possibilité énoncée ci-dessus en redéfinissant le but de la science : notre vœu est de formuler un ensemble de lois qui soient capables de prédire les événements seulement dans les limites du principe d’incertitude.
La seconde possibilité, celle qui évoque une série infinie de théories de plus en plus raffinées, est en accord avec notre expérience. En plusieurs occasions, nous avons accru la sensibilité de nos mesures ou conduit une nouvelle classe d’observations seulement pour découvrir de nouveaux phénomènes qui n’étaient pas prédits par la théorie existante, et pour prendre en compte ceux-ci, nous avons eu à développer une théorie plus avancée. Ce ne serait donc pas très surprenant que la génération actuelle de théories de la grande unification ait tort en affirmant que rien d’essentiel ne pourra plus arriver entre l’énergie d’unification électrofaible d’environ 100 GeV et l’énergie de grande unification d’environ un million de milliards de GeV. Nous devrions vraiment nous attendre à trouver plusieurs nouvelles couches de structures plus fondamentales que les quarks et les électrons que nous appelons actuellement particules « élémentaires ».
Cependant, il semble que la gravité puisse fournir une limite à cette séquence de « poupées russes ». Si l’on avait une particule avec une énergie supérieure à l’énergie de Planck, dix milliards de milliards de GeV (un 1 suivi de 19 zéros), sa masse serait si concentrée qu’elle se retrancherait elle-même du reste de l’univers et qu’elle formerait un trou noir. Donc il semble vraiment que la séquence de théories de plus en plus raffinées doive connaître quelque limite au fur et à mesure que nous augmentons les énergies et qu’il devrait y avoir une théorie ultime de l’univers. Bien sûr, l’énergie de Planck représente un long chemin à partir des énergies d’environ une centaine de GeV qui sont ce que l’on peut produire de mieux au laboratoire aujourd’hui. Nous ne comblerons pas cette lacune avec les accélérateurs de particules dans les années à venir ! Les stades très primitifs de l’univers, cependant, sont une arène où de telles énergies ont pu se déployer. Je pense qu’il y a de bonnes chances pour que l’étude de l’univers primitif et les exigences de la logique mathématique nous amènent à une théorie complètement unifiée durant la vie de certains de ceux qui nous entourent aujourd’hui, à condition toutefois que nous n’explosions pas auparavant.
Qu’est-ce que cela signifierait si nous découvrions aujourd’hui la théorie ultime de l’univers ? Comme nous l’avons expliqué dans le chapitre 1, nous ne pourrions pas être tout à fait sûrs d’avoir trouvé vraiment la théorie correcte, puisque les théories ne peuvent être prouvées. Mais si la théorie est valable mathématiquement et donne des prédictions qui collent toujours aux observations, nous pourrions avoir raisonnablement confiance en elle. Cela mènerait à son terme un long et glorieux chapitre de l’histoire de la lutte intellectuelle de l’humanité pour comprendre l’univers. Mais cela révolutionnerait également pour chacun la compréhension ordinaire des lois qui gouvernent l’univers. À l’époque de Newton, il était possible pour l’honnête homme d’avoir un aperçu de l’ensemble du savoir humain, au moins dans ses grandes lignes. Mais depuis lors, l’allure du développement de la science a rendu cela impossible. Parce que les théories sont toujours modifiées pour tenir compte de nouvelles observations, elles ne sont jamais réellement digérées ou simplifiées de telle sorte que tout un chacun puisse les comprendre. Vous devez être spécialiste pour y arriver ; et encore, vous ne pourrez qu’espérer avoir votre propre aperçu d’une petite partie des théories scientifiques. Qui plus est, le rythme des progrès est si élevé que ce que vous aurez appris à l’école ou à l’université sera toujours un peu dépassé. Seules quelques personnes peuvent se maintenir à la frontière toujours mouvante du savoir, consacrer tout leur temps à cela et se spécialiser dans une petite zone. Le reste de la population a une bien petite idée des progrès accomplis ou de l’excitation qu’ils ont produite. Il y a soixante-dix ans, si l’on en croit Eddington, deux personnes seulement comprenaient la théorie de la Relativité Générale. De nos jours, des dizaines de milliers de diplômés de l’université l’apprennent et plusieurs millions de gens sont plus ou moins familiarisés avec cette notion. Si une théorie complètement unifiée est découverte, ce ne sera qu’une question de temps avant qu’elle soit digérée, simplifiée et enseignée, au moins dans ses grandes lignes. Nous serions alors tous capables d’avoir quelque compréhension des lois qui gouvernent l’univers et qui sont responsables de notre existence.
Même si nous découvrons une théorie complètement unifiée, cela ne signifierait pas que nous serions capables de prédire les événements en général, cela pour deux raisons. La première, c’est la limitation que le principe d’incertitude de la mécanique quantique confère à nos pouvoirs de prédiction. Dans la pratique, cependant, cette première limitation est moins restrictive que la seconde. Cela vient du fait que nous ne pouvons résoudre les équations de la théorie exactement, sauf dans des situations très simples. (Nous ne pouvons même pas résoudre exactement le mouvement de trois corps dans la théorie newtonienne de la gravitation, et la difficulté croît avec le nombre de corps et la complexité de la théorie.) Nous connaissons déjà les lois qui gouvernent le comportement de la matière dans les conditions presque les plus extrêmes. En particulier, nous connaissons les lois fondamentales qui sous-tendent toute la chimie et la biologie. Mais nous n’avons certainement pas réduit ces sujets au statut de problèmes résolus ; nous avons, comme toujours, peu de succès lorsque nous prédisons le comportement humain à partir d’équations mathématiques ! Aussi, même si nous trouvons un ensemble de lois fondamentales, il y aura toujours dans les années qui suivront un souci intellectuel de développer de meilleures méthodes d’approximation de telle sorte que nous puissions faire de meilleures prédictions concernant les conséquences probables des situations complexes et réelles. Une théorie complète, logique et unifiée n’est que le premier pas : notre but est une complète compréhension des événements autour de nous et de notre propre existence.