

МЕЖПЛАНЕТНЫЕ ПУТЕШЕСТВИЯ
полеты в мировое пространство и достижение небесных светил
с 15 рисунками
ИЗДАНИЕ ЧЕТВЕРТОЕ ПЕРЕРАБОТАННОЕ И ПОПОЛНЕННОЕ
АКАДЕМИЧЕСКОЕ ИЗДАТЕЛЬСТВО
ПЕТРОГРАД : 1923
Сочинения Я. И. Перельмана.
Занимательная физика. Книги 1-я и 2-я. 1922 г. 5-е изд. (55 — 70 тыс. экземпляров).
Физическая хрестоматия. Ч. 1-я. 1922. Ч. 2-я. 1923. (1 — 15 тыс. экз.).
Межпланетные путешествия. 1923. 4-е изд. (36—40 тыс.).
Далекие миры. Физическое описание планет. 1919. 2-е изд. (16 — 20 тыс. экземпляров).
Новый задачник по геометрии. 1923. (15 — 30 тыс.).
Реальное направление в шкальной геометрии. 1923.
Новые и старые меры. 1923. 3-е изд. (20—140 тыс. экз.).
Метрическая система. Обиходный справочник. 1923. (1 — 10 тыс. экземпляров).
Веселые задачи. 1919. 2-е изд. (5 — 45 тыс. экз.).
Загадки и диковинки в мире чисел. 1923.
Герберт Уэльс. „Первые люди на Луне" (обработанный перевод). 1923. 2-е изд.
ГРАФИЧЕСКИЕ МАСТЕРСКИЕ АКАДЕМИЧЕСКОГО ИЗДАТЕЛЬСТВА

ПЕТРОГРАД.
KOBEНСКИЙ, 2
Главлит № 3205 4000 экз.
Предисловие
Мыслимо, а следовательно возможно, что человек полетит когда-нибудь до отдаленнейших светил.
Мысль о полетах в глубины вселенной и достижении иных миров автор не считает праздной мечтой. Она полна высокого интереса для науки и для жизни. Было время, когда признавалось невозможным переплыть океан; нынешнее всеобщее убеждение в недосягаемости небесных светил, в сущности, не более обосновано, нежели вера наших предков в недостижимость антиподов. Правильный путь к разрешению проблемы заатмосферного летания и межпланетных путешествий уже намечен, — к чести русской науки, трудами русского ученого. Практическое же разрешение этой грандиозной задачи, невыполнимое сейчас, может осуществиться не в столь далеком будущем.
Этой маленькой экскурсией в область космической физики автор надеется также до некоторой степени рассеять существующее в публике предубеждение против небесной механики и физики, как знаний слишком отвлеченных, неспособных будто бы дать пищу живому уму. Наука, которая открывает возможность успешно соперничать в полете воображения с фантазией остроумнейших романистов, проверять и исправлять их смелые замыслы, наука, указывающая пути осуществления величайших грез человечества, должна перестать казаться сухой и скучной. И если те простейшие сведения из этой области знания, которые рассеяны в настоящей книге, заронят в уме любознательного читателя искру интереса к изучению механики и физики вселенной, если они возбудят желание поближе познакомиться с фундаментом величественной науки о небе, то цель автора будет достигнута вполне.
Чтение этой книги не требует никаких специальных познаний. Материал, предназначаемый для более подготовленных читателей, отнесен в отдел „Прибавлений".
Я. П.
Август, 1915.
Второе и третье издания книжки (под заглавием: „Путешествия на планеты") были заново проредактированы автором. В целях придания тексту большей ясности некоторые места книги развиты были подробнее, другие — черезчур отвлеченные — исключены. Число рисунков увеличено. Отдел „Прибавлений" пополнен проектом летательного прибора известного революционера Н. И. Кибальчича, которому, по справедливости, принадлежит первенство в разработке идеи аппарата, способного летать вне атмосферы.
Я. П.
Январь, 1919.
При просмотре и подготовке текста для настоящего, 4-го, издания были проверены все приведенные в книге расчеты и числовые данные. Заново переработан и значительно пополнен отдел „Прибавлений"; в него включены: параграф о теории тяготения Эйнштейна, заметки о поглощении тяготения, о новейших успехах артиллерии, о проекте Графиньи, о жизни в среде без тяжести, статья о межпланетной сигнализации; приведены новые расчеты, относящиеся к перелету Жюль-Вернова ядра; сообщается более подробно о проектах Кибальчича и Циолковского; расширена статья о невесомости падающих тел, и др.
В настоящем издании восстановлено первоначальное заглавие книжки, история которого не лишена поучительности. В 1915 г. заглавие „Межпланетные путешествия", данное мною первому изданию этой книжки, звучало для многих настолько ново и малопонятно, что в следующих двух изданиях, вышедших в 1919 г., я отказался от него, заменив более ясным „Путешествия на планеты". Но уже за короткий срок, к 1923 г., термин ,,межпланетные путешествия" успел сделаться общеупотребительным не только в авиационной, но и в общей литературе. Это, несомненно свидетельствует о том, что и самая идея межпланетных перелетов быстро приобретает популярность.
Июнь, 1923.
Я. П.
I.
Величайшая греза человечества
Проложенная Ньютоном дорога
Страданий облегчила тяжкий гнет;
С тех пор открытий сделано уже много,
И верно мы к Луне когда-нибудь,
Благодаря парам, направим путь.
Очередная задача техники
Суждено ли нам когда-нибудь совершать путешествия на другие планеты, или же мы обречены навеки оставаться пленниками земного шара? Мысль о странствовании в межзвездных пустынях, о перелетах с планеты на планету — в настоящее время, конечно, не более, как заманчивая греза. Рассуждать на эту тему можно пока разве лишь так, как говорили об авиации в эпоху Леонардо да-Винчи, целые века тому назад. Но ведь авиация на наших глазах из красивой мечты превратилась в повседневную действительность. Отчего же не допустить, что со временем осуществится и мечта о космических путешествиях, что наступит день, когда небесные дирижабли ринутся в глубь вселенной и перенесут бывших пленников Земли на Луну, на планеты, — даже, быть-может, в системы других солнц, далеких звезд?.. И кто знает, среди нынешних робких попыток мысленно разрешить эту грандиозную проблему — не намечается ли уже такая идея, которой впоследствии суждено воплотиться в реальную форму?
Попробуем с этой точки зрения рассмотреть наиболее заслуживающие внимания проекты космических путешествий, высказанные хотя бы и в форме фантастического романа. Быть-может, у кого-нибудь из мечтателей-романистов мы найдем намек на то, в каком направлении техника должна искать путей к осуществлению одной из величайших грез человечества.
Лет двести-триста тому назад, когда и воздухоплавание было только фантастической грезой, вопрос о межзвездных полетах казался тесно связанным с проблемой летания в атмосфере, Однако, мы уже путешествуем в воздухе, перелетаем над реками, горными хребтами, пустынями, морями; смело летим через материки и океаны, добились сказочных успехов в деле летания по воздуху, — а между тем полеты в мировое пространство попрежнему еще далеки от осуществления.
Заатмосферное летание
Но иначе и быть не может: ведь это две совершенно различные проблемы...... — летать в воздухе и летать в пустоте.
С точки зрения механики, аэроплан движется так же, как и пароход или паровоз: колеса паровоза отталкиваются от рельсов, винт парохода — от воды, а пропеллер аэроплана отталкивается от воздуха. Но в заатмосферных пустынях, в мировом пространстве, нет воздуха, нет вообще никакой среды, на которую можно было бы так или иначе опираться. Значит, чтобы осуществить межпланетные полеты, техника должна обратиться к иным принципам летания и выработать такой тип снаряда, который мог бы передвигаться в совершенно пустом пространстве, не имея никакой опоры кругом себя. Такое „заатмосферное летание" не может иметь ничего общего с современной авиацией. Для разрешения этой задачи техника должна искать совершенно иных путей.
II.
Всемирное тяготение и земная тяжесть
Прежде чем приступить к этим поискам, уделим минуту внимания тем невидимым цепям, которые приковывают нас к земному шару, — познакомимся поближе с действием силы всемирного тяготения. Ведь с нею-то и предстоит, главным образом, иметь дело будущим плавателям мирового океана.
Тяготение
Всемирное тяготение ни на мгновение не перестает проявляться везде и всюду, на каждом шагу, в великом и в малом. „Падение яблока с дерева, провал моста, сцепление почвы, явления прилива, предварения равноденствий, орбиты планеты со всеми их возмущениями, существование атмосферы, солнечное тепло, вся область астрономического тяготения, также как форма наших домов и мебели, совокупность условий обыденной жизни и даже наше существование — всецело зависят от этого основного свойства вещества", — картинно изображает значение тяготения в природе английский физик проф. О. Лодж. Каждые две частицы любого вещества притягивают друг друга, — и никогда, ни при каких условиях это взаимное притяжение не прекращается: оно лишь ослабевает с расстоянием, но не уничтожается от времени.
Притяжение двоих людей
Как же велика эта сила взаимного притяжения тел? Она может быть и невообразимо ничтожна и чудовищно могущественна, — в зависимости от размеров притягивающихся масс и от их взаимного расстояния. Два взрослых человека, отстоящие на сажень один от другого, взаимно притягиваются с силой менее чем 1/100 миллиграмма. Столь ничтожная сила, в тысячу раз меньшая веса мухи, ничем, конечно, не может обнаружиться в условиях обыденной жизни. Она недостаточна даже для того, чтобы разорвать паутинную нить; а ведь, чтобы сдвинуть человека с места, нужно преодолеть трение его подошв о пол; для груза в 4—5 пудов сила трения достигает целого пуда, т.-е. в 2.000 миллионов раз больше, чем упомянутая сила взаимного притяжения двух человеческих тел. Удивительно ли, что в условиях обыденной жизни мы не замечаем на Земле взаимного тяготения предметов[1]?
Но если бы трения не было, если бы два человеческих существа висели без опоры в пустом пространстве и ничто не мешало проявляться их взаимному притяжению, — то какие бы чувства ни питали эти люди друг к другу, они непреодолимо влеклись бы один к другому силою всемирного тяготения. Правда, скорость этого сближения, под действием столь ничтожной силы, была бы мала до смешного. В течение первого часа каждое тело переместилось бы навстречу другому всего на 1½ сант. В продолжение второго часа перемещение было бы немного значительнее, но в общем до сближения обоих тел вплотную прошло бы не менее пяти часов. И все-таки, очутись эти двое людей где-нибудь в мировом пространстве (в достаточном удалении от других притягивающих тел), они могли бы образовать нечто в роде темной миниатюрной двойной звезды: сообщив одному из тел ничтожный боковой толчок, мы заставили бы оба тела медленно обращаться вокруг их общего центра тяжести, лениво проползая 1/10 сант. в минуту и заканчивая полный оборот в двое суток.
Притяжение двух кораблей
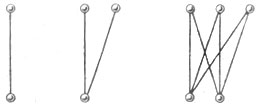
Всемирное притяжение
Закон масс — притяжение пропорционально произведению притягивающихся масс.
1 единица массы притягивает 1 единицу с силою 1 ед.
2 единицы массы притягивают 1 единицу с силою 2 ед.
3 единицы массы притягивают 2 единицы с силою 6 ед.
Увеличьте притягивающиеся массы — и сила их взаимного тяготения заметно возрастет. Провозглашенный Ньютоном закон всемирного тяготения гласит, что „притяжение тел увеличивается пропорционально произведению их масс и уменьшается пропорционально квадрату их расстояния". Можно вычислить, что два дредноута, весом по 25.000 тонн каждый, плавая на расстоянии одной версты один от другого, взаимно притягиваются с силою в 1 золотник. Это почти в полмиллиона раз больше упомянутой силы взаимного притяжения двух человеческих тел, но, разумеется, еще слишком недостаточно, чтобы преодолеть трение кораблей о воду и сблизить их вплотную. Ведь именно для преодоления трения корабля о воду предназначены могучие пароходные машины. Но и при отсутствии трения оба дредноута силою взаимного притяжения сблизились бы в течение первого часа всего только на два сантиметра.
Притяжение двух миров
Зато для таких огромных масс, как целые солнца и планеты, взаимное притяжение даже на гигантских расстояниях достигает степеней, превосходящих человеческое воображение.
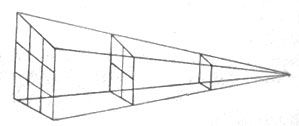
Всемирное притяжение
Закон расстояний — притяжение убывает пропорционально квадрату расстояния.
На двойном расстоянии притяжение уменьшается в 2х2, т.-е. в 4 раза, на тройном — в 3х3, т.-е. в 9 раз, и т.д.

Наша Земля, несмотря на неимоверную отдаленность от Солнца, удерживается на своей орбите единственно лишь могучим взаимным притяжением этих обоих тел. Предположите на минуту, что солнечное притяжение внезапно прекратилось, и что земные инженеры задались целью заменить невидимые цепи тяготения материальными связями, т.-е. попросту желают привязать земной шар к Солнцу стальными канатами. Вы видели, конечно, те свитые из проволоки канаты, на которых висят наши лифты. Каждый из них способен выдержать тяжесть свыше тысячи пудов. Знаете ли, сколько понадобилось бы таких канатов, чтобы заменить ими взаимное притяжение Земли и Солнца? Цифра с пятнадцатью нулями ничего не скажет вашему воображению. Вы получите более наглядное представление о могуществе этого притяжения, если я скажу вам, что вся обращенная к Солнцу поверхность земного шара была бы густо покрыта непроходимым лесом этих канатов, по тридцати на каждый квадратный аршин!
Вот как огромна та невидимая сила, которая притягивает планеты к Солнцу.
Но для межпланетных полетов вовсе не понадобится рассекать эту связь миров и сдвигать небесные светила с их вековечных путей. Будущему моряку вселенной придется считаться лишь с притягательным действием планет на мелкие тела, и прежде всего, конечно, с напряжением тяжести близ земной поверхности: только оно и приковывает нас к нашей планете.
Свободное падение
Земная тяжесть интересует нас в данный момент не потому, что она заставляет каждое лежащее или подвешенное земное тело давить на свою опору. Для нас важнее то, что всем не имеющим опоры телам она сообщает движение „вниз", т.-е. к центру Земли. Вопреки обычному мнению, для всех тел — тяжелых и легких — скорость этого движения, в пустом пространстве, одинакова и по истечении первой секунды падения всегда равна 10 метрам [2].
По истечении второй секунды падения, к уже имеющейся 10-метровой скорости присоединяются еще 10 метров: скорость удваивается. Возрастание скорости длится все время, пока совершается падение. С каждой секундой скорость падения возрастает на одну и ту же величину — именно на 10 метров. Поэтому к концу третьей секунды она уже равна 30 метрам, и т. д. Если же тело брошено снизу вверх, то скорость его взлета, наоборот, уменьшается каждую следующую секунду на те же 10 метров: по истечении первой секунды она уже на 10 метров меньше, чем первоначальная; к концу второй — еще на 10 метров, т.-е. уже на 20 метров, и т. д., пока не истощится вся первоначально сообщенная ему скорость, и тело не начнет падать вниз. (Так происходит лишь до тех пор, пока тело, поднимаясь вверх, не слишком значительно удаляется от земной поверхности; на большом расстоянии от Земли напряжение тяжести заметно ослабевает, и тогда ежесекундно будет отниматься уже не 10 метров, а меньше).
Сухие цифры, — но они должны нам многое пояснить.
Невидимые оковы тяжести
В старину, говорят, к ноге каторжника приковывали цепь с тяжелой гирей, чтобы отяжелить его шаг и сделать неспособным к побегу. Все мы, жители Земли, незримо отягчены подобною же гирею, мешающей нам вырваться из земного плена в окружающий простор вселенной. При малейшем усилии подняться ввысь эта невидимая гиря дает себя чувствовать и влечет нас вниз с возрастающей стремительностью. Быстрота нарастания этой скорости падения — по 10 метров в каждую секунду, — может служить точною мерою напряжения тяжести на земной поверхности и характеризует отягчающее действие той невидимой гири, которая держит нас в земном плену.
Все мечтающие о полетах по беспредельному океану вселенной, — а какой из пытливых умов не мечтает о них? — должны глубоко сожалеть о том, что человеческому роду приходится жить как-раз на той планете, которую мы именуем „Землей". Среди всех небесных сестер земного шара лишь немногие обладают столь значительным напряжением тяжести, как именно наша планета. Взгляните на прилагаемую табличку, где напряжение тяжести на разных планетах солнечной системы дано по сравнению с напряжением земной тяжести, принятым здесь за единицу:
Вы видите, что из планет нашей солнечной системы только на двух, гигантах Юпитере и Сатурне, напряжение тяжести превосходит земное. На всех же остальных планетах оно слабее. Если бы условия тяжести были у нас такие, как на Марсе или на Луне, то, пожалуй, не пришлось бы теперь писать книг в роде этой, потому что люди давно уже путешествовали бы по мировому пространству. А на мелких астероидах достаточно было бы просто оттолкнуться от планеты, чтобы унестись навеки в необъятный простор вселенной...
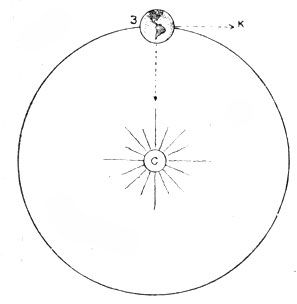
Земля в каждый момент, вследствие инерции, стремится двигаться по прямой линии, касательной к ее действительной орбите, и только притяжение Солнца заставляет ее уклоняться от касательной, чтобы следовать по криволинейному пути. (Масштаб не соблюден).

Итак, вопрос о возможности межпланетных путешествий сводится к вопросу о том, какими способами мыслимо бороться с силою земного притяжения.
III.
Борьба с тяготением
Мысль наша способна вообразить лишь троякого рода борьбу с земною тяжестью:
1) Можно искать средств укрыться или заслониться от силы притяжения, сделаться для нее неуязвимым:
2) Можно пытаться в достаточной степени ослабить напряжение земной тяжести.
И, наконец,—
3) Оставляя без изменения силу земной тяжести, можно изыскивать средства преодолеть ее.
Каждый из этих трех путей в случае успеха сулит нам возможность освободиться из плена земной тяжести и пуститься в свободное плавание по океану вселенной.
В этой последовательности мы и будем рассматривать здесь наиболее любопытные, наиболее заманчивые или наиболее поучительные проекты осуществления космических путешествий.


При исчезновении силы тяготения „гигантские пушки взлетали бы на воздух, как мыльные пузыри"...
IV.
Можно ли укрыться от силы тяжести?
Мы слишком привыкли к тому, что все вещи, все физические тела прикованы своим весом к земле; нам трудно поэтому даже мысленно отрешиться от силы тяжести и представить себе картину того, что было бы, если бы мы обладали способностью уничтожать эту силу по своему желанию. Такую фантастическую картину нарисовал недавно в одной из своих статей американский ученый Г. Сервис[3].
„Если бы, — писал этот ученый, — в самый разгар военной кампании мы могли посылать волны, которые, нейтрализовали бы силу тяжести, то всюду, куда бы они ни попадали, немедленно наступал бы хаос. Гигантские пушки взлетали бы на воздух, как мыльные пузыри. Марширующие солдаты вдруг почувствовали бы себя легче перышка и беспомощно поплыли бы в воздухе, как пробка на воде, будучи всецело во власти неприятеля, находящегося вне сферы действия этих волн. Картина смешная и, как может показаться, невероятная, — а между тем так было бы в действительности, если бы людям удалось подчинить силу тяжести своей власти". (Мы приводим здесь заимствованную из того же американского журнала попытку художника изобразить наглядно это необычайное зрелище).
Более того: власть над силой тяготения позволила бы человеку по своему желанию изменить устройство вселенной.
Всепроницаемость тяготения
„Если бы, — продолжает упомянутый ученый, — удалось нейтрализовать всю Землю (т.-е. уничтожить на ней силу тяжести), то она могла бы покинуть нашу солнечную систему и присоединиться к системе какой-нибудь другой звезды. А если бы случилось, что какая-нибудь комета стала угрожать Земле гибелью, то можно было бы, нейтрализовав эту комету, заставить ее свернуть с своего пути и тем отвратить гибель Земли".
Все эти заманчивые возможности — не более, как фантазия. Мы пока и мечтать не можем о том, чтобы распоряжаться силою тяготения по своему желанию. Мы не в состоянии даже хоть сколько-нибудь отклонить эту силу от пути, по которому она распространяется, не можем ни одного тела защитить от всюду проникающего ее действия.

Если бы мы могли посылать волны, которые нейтрализовали бы силу тяжести"...
Всемирное тяготение — единственная сила природы, для распространения которой мы не знаем никаких преград. Какое бы огромное, какое бы плотное тело ни стояло на ее пути, — сила эта проникает сквозь него совершенно так же, как через пустое место. Для тяготения не существует «непрозрачных» тел — нам пока еще такое тело неизвестно. Точные вычисления не обнаружили ни малейшего ослабления притягательной силы от прохождения ее через вещество тел. (Правда, в самые последние годы возникли кое-какие сомнения на этот счет, но пока только в виде подозрений и предположений — см. прибавление 2-ое в конце книги). Можно, однако, мечтать о том, что в будущем гению человеческому посчастливится отыскать такое непроницаемое для тяготения вещество или приготовить его искусственно. Не сможем ли мы тогда с его помощью укрыться от силы притяжения, сбросить с себя на время докучные цепи тяжести и свободно ринуться с Земли в бездны мирового пространства?
Заслон от силы тяжести
Остроумный английский писатель Герберт Уэльс подробно развил эту мысль в научно-фантастическом романе „Первые люди на Луне"[4].
Ученый герой романа, изобретатель Кевор, открыл способ изготовления именно такого вещества, непроницаемого для тяготения. Об этом фантастическом веществе, названном в романе „кеворитом", автор рассуждает так (ведя речь от лица другого своего героя).
„Кевор стремился найти такое вещество, которое было бы „непрозрачно" для всех форм лучистой энергии. Почти каждое тело отличается непрозрачностью для какого-либо рода лучистой энергии и прозрачно для других ее видов. Стекло, например, пропускает видимый свет, но для невидимых лучей, производящих нагревание, оно гораздо менее прозрачно; квасцы, прозрачные для видимых лучей света, полностью задерживают лучи невидимые, нагревающие. Напротив, раствор иода в жидкости, называемой сероуглеродом, непрозрачен для видимых лучей света, но свободно пропускает невидимые, греющие лучи: через сосуд с такой жидкостью не видно пламени, но хорошо ощущается его теплота. Металлы непрозрачны не только для лучей света — видимого и невидимого — но и для электрических колебаний, которые, однако, свободно проходят сквозь стекло или через упомянутый раствор, как сквозь пустое пространство. И т. п.
„Далее. Мы знаем, что для всемирного тяготения, т.-е. для силы тяжести, проницаемы все тела. Вы можете поставить преграды, чтобы отрезать лучам света доступ к предметам; помощью металлических листов можете оградить предмет от доступа электрических волн искрового телеграфа, — но никакими преградами не можете вы защитить предмет от действия тяготения Солнца или от силы земной тяжести. Почему собственно в природе нет подобных преград для тяготения — трудно сказать. Однако, Кевор не видел причин, почему бы и не существовать такому веществу, непроницаемому для тяготения; он считал себя способным искусственно создать такое непроницаемое для тяготения вещество.
„Всякий, обладающий хоть искрой воображения, легко представит себе, какие необычайные возможности открывает перед нами подобное вещество. Если, например, нужно поднять груз, то как бы огромен он ни был, достаточно будет разостлать под ним лист из этого вещества — и груз можно будет поднять хоть соломинкой".
Обладая таким замечательным веществом, герои романа сооружают небесный дирижабль, в котором и совершают смелый перелет на Луну. Устройство снаряда весьма несложно: в нем нет никакого двигательного механизма, так как он перемещается действием внешней силы.
Вот описание этого фантастического снаряда:
Межпланетный дирижабль Уэльса
„Вообразите себе шарообразный снаряд, достаточно просторный, чтобы вместить двух человек с их багажом. Снаряд будет иметь две оболочки — внутреннюю и наружную; внутренняя из толстого стекла, наружная — стальная. "Можно взять с собою запас сгущенного воздуха, концентрированной пищи, аппараты для дестилляции воды и т. п. Стальной шар будет весь снаружи покрыт слоем кеворита. Внутренняя стеклянная оболочка будет сплошная, кроме люка; стальная же будет состоять из отдельных частей, и каждая такая часть может сворачиваться, как штора. Это легко устроить посредством особых пружин; шторы можно будет опускать и свертывать электрическим током, проводимым по платиновым проводам в стеклянной оболочке. Все это уже технические подробности. Главное то, что наружная оболочка снаряда будет вся состоять как бы из окон и „кеворитных" штор. Когда все шторы наглухо спущены, внутрь шара не может проникнуть ни свет, никакой вообще вид лучистой энергии, ни сила всемирного тяготения. Но вообразите, что одна из штор поднята — тогда какое-нибудь весомое тело, которое случайно находится вдали против этого окна, притянет нас к себе. Практически мы сможем путешествовать в мировом пространстве в том направлении, в каком пожелаем, притягиваемые то одним, то другим небесным телом".
Как видим, шар Уэльса, не имея внутри себя никакого двигателя, все же вполне приспособлен для межпланетных странствований...
Интересен у романиста самый момент отправления этого снаряда в путь. По идее Уэльса, тонкий слой „кеворита", покрывающий наружную поверхность снаряда, делает его совершенно невесомым. Невесомое тело не может спокойно лежать на дне воздушного океана; с ним должно произойти то же, что произошло бы с пробкой, погруженной на дно озера: пробка быстро всплывает на поверхность воды. Точно также невесомый снаряд, — отбрасываемый, к тому же, еще и инерцией вращающегося земного шара, — должен стремительно подняться ввысь и, дойдя до крайних границ атмосферы, умчаться по инерции в мировое пространство. Герои романа Уэльса так и полетели. И, очутившись далеко за пределами атмосферы, они, открывая одни заслонки, закрывая другие, подвергая свой снаряд притяжению то Солнца, то Земли, то Луны, — постепенно добрались до поверхности нашего спутника. А впоследствии точно таким же путем снаряд благополучно возвратился на Землю.
Этот проект небесных путешествий, так заманчиво представленный в романе, невольно подкупает своей внешней простотой. На первый взгляд он кажется настолько правдоподобным, что естественно возникает мысль: не заложено ли в нем здоровое зерно, и не в этом ли направлении следует искать разрешения задачи межпланетных путешествий? Нельзя ли, в самом деле, изобрести вещество, непроницаемое для тяготения, и, пользуясь им, устроить космический дирижабль?
Стоит, однако, вдуматься поглубже в эту идею, чтобы убедиться в ее полной несостоятельности.
Самая загадочная сила природы
Не говорю уже о том, как мало у нас надежды найти когда-нибудь вещество, непроницаемое для тяготения. Причина тяготения нам неизвестна: со времен Ньютона, открывшего эту силу, мы ни на шаг не приблизились к познанию ее внутренней сущности. Без преувеличения можно сказать, что тяготение — самая загадочная из всех сил природы. Мгновенная быстрота, с которой она, повидимому, распространяется, лишает нас возможности придумать удовлетворительное объяснение ее сущности[5].
Столь же непостижимо и то, что тяготение изменяется сообразно не поверхности тела, не его объему, а массе, т.-е. способности тела приобретать большее или меньшее ускорение под действием силы. При таких условиях ставить решение проблемы небесных путешествий в зависимость от изобретения фантастического экрана (заслона) для тяготения — значит обречь себя на неопределенно долгое, быть-может, и бесплодное ожидание.
Но пусть даже заслон тяготения — фантастический „кеворит" — найден, пусть с его помощью сооружен снаряд по проекту английского романиста. Пригоден ли будет этот снаряд для межпланетных путешествий, как описано в романе? Посмотрим.
Смущает нас, прежде всего, скорость. Там, где маршруты исчисляются сотнями тысяч и миллионами верст, от экипажа, естественно, требуется огромная быстрота перемещения. Между тем, по этой части с нашим межпланетным дирижаблем обстоит далеко неблагополучно. В самом деле, какая сила движет и управляет снарядом Уэльса? Сила притяжения различных небесных тел. Но мы уже знаем, что на больших расстояниях эта сила способна сообщить небольшому телу в первые часы лишь весьма умеренную скорость. Можно было бы доказать несложным вычислением, что под действием одного лишь лунного притяжения предмет с расстояния Земли должен падать на Луну больше 43 дней!
Своим притяжением Луна может заставить предмет, находящийся от нее на расстоянии Земли, передвинуться в первую секунду всего лишь на несколько тысячных долей дюйма. Под действием Солнца то же тело переместилось бы в первую секунду на 1/8 дюйма. Влияние притяжения далеких планет, а тем более — звезд, на наш фантастический снаряд было бы исчезающе ничтожно[6].
И хотя полученная снарядом скорость увеличивается с каждой секундой, — все же пришлось бы ждать целые часы, целые сутки, чтобы снаряд накопил скорость, хоть сколько-нибудь сравнимую с теми гигантскими расстояниями, которые придется преодолевать в межпланетных пустынях[7].
Экран тяготения и вечный двигатель
Мы подходим к самому убийственному доводу против проекта английского романиста, к первородному греху его основной идеи. В уме читателя, вероятно, уже мелькнула тень сомнения, когда романист говорил нам о возможности поднять тяжелый груз „хоть соломинкой", поместив под ним непроницаемый для тяготения экран. Да ведь это же значит ни более ни менее, как разрешить древнюю проблему вечного двигателя, создать энергию „из ничего"! Вообразите, в самом деле, что мы уже обладаем экраном тяготения. Тогда мы подкладываем этот экран под любой груз, поднимаем, без всякой затраты энергии, наш теперь уже невесомый груз на любую высоту и затем снова убираем экран. Груз, конечно, падает вниз и может произвести при падении некоторую работу. Мы повторяем эту простую операцию дважды, трижды, тысячу, миллион раз, сколько пожелаем — и получаем произвольно большое количество энергии, не заимствуя ее ниоткуда!..
Выходит, что непроницаемый для тяготения экран дает нам чудесную возможность создать энергию, сотворить ее „из ничего", ибо ее появление, повидимому, не сопровождается одновременным исчезновением равного количества энергиии в какой-нибудь иной форме или— в другом месте. Если бы герой Уэльса, действительно, побывал на Луне и возвратился на Землю тем способом, какой описан в романе, то в результате подобного путешествия мир обогатился бы новым запасом энергии. Общее количество ее во вселенной увеличилось бы ровно на столько, сколько составляет разность работ, совершаемых силою тяжести при падении человеческого тела с Луны на Землю и с Земли на Луну. Земля притягивает сильнее, чем Луна, и, следовательно, первая работа больше второй. Пусть этот прирост энергии ничтожен по сравнению с неисчерпаемым запасом ее во вселенной — все же такое сотворение энергии есть несомненное чудо, противоречащее основному закону природы, который гласит:
„Общий запас энергии во вселенной ни при каких обстоятельствах не увеличивается и не уменьшается, а остается постоянным".
Если мы пришли к столь явному противоречию с законами природы, к возможности создавать энергию „из ничего", — то это по-просту значит, что в наше рассуждение вкралась незамеченная нами основная ошибка. Нетрудно понять, где именно надо эту погрешность искать. Идея экрана, непроницаемого для тяготения, сама по себе нисколько не нелепа; но ошибочно думать, будто помощью его можно сделать тело невесомым, не затрачивая при этом никакой энергии. Нельзя перенести тело за экран тяготения, не производя никакой работы. Невозможно задвинуть шторы „кеворитного" шара, не применяя силы. То и другое должно сопровождаться затратой определенного количества энергии, равного тому количеству ее, которое потом является словно созданным „из ничего". В этом и состоит разрешение загадки, к которой мы пришли.
Задвигая заслонки своего межпланетного снаряда, герои Уэльса тем самым словно рассекали невидимую цепь притяжения, которая приковывала их тела к Земле. Мы в точности знаем крепость этой цепи и можем вычислить величину работы, необходимой для ее разрыва. Это та работа, которую вы совершили бы, если бы перенесли весомое тело с земной поверхности в бесконечно удаленную точку пространства, где сила земного притяжения равна нулю.
Большинство людей привыкло относиться к слову „бесконечность" с мистическим благоговением, и упоминание этого слова нередко порождает в уме не-математика совершенно превратные представления. Когда я упомянул о работе, производимой телом на бесконечном пути, многие читатели, без сомнения, уже решили про себя, что работа эта бесконечно велика. На самом же деле она хотя и очень велика, но имеет значение конечное, которое математик может в точности вычислить. Работу перенесения весомого тела с земной поверхности в бесконечность мы можем рассматривать как сумму бесконечного ряда слагаемых, которые быстро уменьшаются, потому что с удалением от Земли сила притяжения беспредельно ослабевает. Сумма таких слагаемых, хотя бы их было и бесчисленное множество, нередко дает результат конечный. Прибавьте к копейке полкопейки, затем еще 1/4 копейки, затем 1/8, потом 1/16, 1/32, и т. д.; вы можете продолжать такой ряд целую вечность, присчитывая все новые и новые прибавки, — и все-таки в результате суммирования получите не более двух копеек! При учете работы тяготения мы имеем нечто в роде подобного сложения, и читатель не должен удивляться, что работа эта даже на бесконечном пути имеет конечное значение. Можно вычислить, что для груза в 1 килограмм работа перенесения гири с земной поверхности в бесконечность составляет немного более 6-ти миллионов „килограммометров". Так как эта техническая оценка работы не для всех понятна, то поясню, что она равна величине работы, которую произвел бы, например, подъемный кран, подняв паровоз с тендером на высоту 30 сажен (100 тонн на высоту 60 метров). Это не бесконечно большая работа, хотя и достаточно значительная для человеческих сил.
Погружение в тень тяготения
В смысле затраты работы совершенно безразлично, перенесете ли вы груз с Земли в бесконечно удаленную точку, или в такое место (хотя бы и весьма близкое), где он вовсе не притягивается Землей. И в том, и в другом случаях вы совершили бы одинаковую работу, ибо величина ее зависит не от длины пройденного пути, а только от различия силы притяжения в крайних точках пути. При переносе тела в бесконечность работа эта производится постепенно, на всем бесконечно длинном пути, а при переносе за экран тяготения такое же количество энергии затрачивается в те несколько мгновений, пока совершается этот перенос. Надо ли говорить, что практически вторую работу было бы гораздо труднее произвести, чем первую?
Теперь становится очевидной безнадежность фантастического проекта Уэльса. Романист не подозревал, что столь простое на вид действие, как перенесение тела за экран, непроницаемый для тяготения — представляет собою неимоверно трудную механическую задачу: ведь для этого надо сделать такое же усилие, как и для того, чтобы удалить тело с Земли в бесконечность!
Уэльс упустил из виду, что задвинуть заслонки его снаряда вовсе не так легко и просто, как захлопнуть дверцу кареты: в тот краткий миг, когда закрывается последняя заслонка и пассажиры отделяются от весомого мира, — должна быть выполнена работа, равная работе перенесения полного веса пассажиров в бесконечность. А так как два человека весят свыше 100 килограммов, то, значит, задвигая заслонки снаряда, герои романа должны совершить работу ни мало, ни много — в 600 миллионов килограммометров! Это почти так же легко выполнить, как втащить броненосец на купол Йсаакиевского собора, и притом в течение всего нескольких секунд. Будь мы были подобными богатырями, мы могли бы без всякого ,,кеворита" буквально прыгнуть с Земли на Луну... Не приходилось бы долго размышлять над проблемой межпланетных путешествий.
Безвыходный круг
Итак, идея странствовать во вселенной под защитою вещества, непроницаемого для тяготения, приводит нас к тому, что в логике называется „безвыходным кругом". Чтобы воспользоваться таким веществом, необходимо преодолеть притяжение Земли — т.-е. выполнить именно то, ради чего и придуман экран тяготения. Следовательно, вещество, непроницаемое для тяготения, бесполезно для небесных путешествий.
V.
Можно ли ослабить земную тяжесть?
Если несбыточны надежды укрыться от силы тяжести, то, быть-может, существуют способы хотя бы ослабить тяжесть на земной поверхности?
Увеличить объем Земли
Казалось бы, простой и ясный закон Ньютона не допускает подобной возможности даже в теории: сила притяжения зависит ведь от массы земного шара, которую уменьшить мы не в состоянии. Однако, это не так. Речь идет о напряжении тяжести на поверхности нашей планеты, а оно, как известно, зависит не от одной лишь массы, но также и от расстояния до центра земного шара, т.-е. от величины земного радиуса. Если бы мы могли разрыхлить земной шар настолько, чтобы, увеличившись в объеме, он имел радиус, например, вдвое больше, чем теперь, то напряжение тяжести на поверхности такого шара стало бы вчетверо меньше. В самом деле: находясь на поверхности Земли, мы были бы вдвое дальше от притягивающего центра (шарообразные тела притягивают так, как будто вся их масса сосредоточена в центре). Выгода от подобного грандиозного переустройства обитаемой нами планеты получилась бы еще и та, что поверхность земного шара увеличилась бы при этом в четыре раза. Людям жилось бы на Земле буквально вчетверо свободнее и вчетверо легче...
Разумеется, ни современная техника, ни, вероятно, и будущая не в состоянии осуществить ничего подобного.
Миллионы лет назад
Любопытно, однако, что некогда, — в древние геологические эпохи, — радиус нашей планеты был действительно больше, нежели теперь; тогда и напряжение тяжести было соответственно слабее. Как утверждают геологи (теория Зюсса), горы на земном шаре образовались вследствие того, что наша планета, охлаждаясь, уменьшалась в объеме; при этом земная кора сморщивалась, как кожа иссохшего яблока. Морщины эти и есть горы. Если мысленно расправить все складчатые горы земного шара, то определится, насколько поверхность нашей планеты была некогда больше, нежели теперь. Этим путем вычислено, что в древнейшую геологическую эпоху (альгонкинскую) радиус земного шара был на 1/4 больше, нежели теперь. Мы знаем, что с удалением от центра напряжение тяжести уменьшается пропорционально квадрату расстояния. Значит, если поверхность Земли была тогда в  дальше от центра, чем теперь, то напряжение тяжести должно измениться в
дальше от центра, чем теперь, то напряжение тяжести должно измениться в  раз, т.-е. составляло приблизительно
раз, т.-е. составляло приблизительно  нынешней силы тяжести. Вы видите, что не всегда тяжесть на Земле была такой, как теперь: миллионы лет тому назад нынешний пуд весил на Земле всего около 25 фунтов. Приходится только пожалеть, что мы не жили на Земле несколькими миллионами лет ранее, когда задачу межпланетных путешествий можно было разрешить легче, нежели теперь...
нынешней силы тяжести. Вы видите, что не всегда тяжесть на Земле была такой, как теперь: миллионы лет тому назад нынешний пуд весил на Земле всего около 25 фунтов. Приходится только пожалеть, что мы не жили на Земле несколькими миллионами лет ранее, когда задачу межпланетных путешествий можно было разрешить легче, нежели теперь...
Ускорить вращение Земли
Механика указывает и другой путь к ослаблению земной тяжести. Этот способ состоит в том, чтобы ускорить быстроту вращения Земли вокруг оси. Уже и теперь центробежная сила, возникающая при вращении земного шара, уменьшает вес всякого тела на экваторе на  долю. В соединении с другой причиной (вздутием земного шара у экватора) центробежная сила действует так, что все тела на экваторе весят на
долю. В соединении с другой причиной (вздутием земного шара у экватора) центробежная сила действует так, что все тела на экваторе весят на  % меньше, чем близ полюсов. Паровоз, весящий в Москве 10.000 пудов, становится по прибытии в Архангельск на 10 пудов тяжелее, а в Одессу — настолько же легче. Партия угля в 300.000 пудов, доставленная с Шпицбергена в какой-нибудь экваториальный порт, уменьшилась бы в весе на 1.200 пудов, если бы приемщику пришла фантазия принять груз, пользуясь пружинными весами, выверенными на Шпицбергене. Броненосец, весивший в Архангельске 20.000 тонн, становится по прибытии в экваториальные воды легче на 80 тонн, т.-е. почти на 5.000 пудов; но это, конечно, остается неощутительным, так как соответственно легче делаются и все другие тела, не исключая и воды в океане. Всю эту разницу веса похищает, главным образом, центробежная сила: на экваторе она несколько больше, чем в высоких широтах, где точки земной поверхности при вращении Земли описывают гораздо меньшие круги.
% меньше, чем близ полюсов. Паровоз, весящий в Москве 10.000 пудов, становится по прибытии в Архангельск на 10 пудов тяжелее, а в Одессу — настолько же легче. Партия угля в 300.000 пудов, доставленная с Шпицбергена в какой-нибудь экваториальный порт, уменьшилась бы в весе на 1.200 пудов, если бы приемщику пришла фантазия принять груз, пользуясь пружинными весами, выверенными на Шпицбергене. Броненосец, весивший в Архангельске 20.000 тонн, становится по прибытии в экваториальные воды легче на 80 тонн, т.-е. почти на 5.000 пудов; но это, конечно, остается неощутительным, так как соответственно легче делаются и все другие тела, не исключая и воды в океане. Всю эту разницу веса похищает, главным образом, центробежная сила: на экваторе она несколько больше, чем в высоких широтах, где точки земной поверхности при вращении Земли описывают гораздо меньшие круги.
Весьма нетрудно доказать, что если бы Земля вращалась в 17 раз быстрее, чем теперь, то центробежная сила на экваторе увеличилась бы 17 X 17, т.-е. почти в 290 раз. Если вы вспомните, что центробежная сила теперь похищает у тел как-раз долю их веса, то поймете, что на экваторе такой быстро вращающейся Земли тела совсем не имели бы веса! Стоило бы тогда лишь достичь экватора, чтобы, слегка оттолкнувшись здесь, быть отброшенным в мировое пространство. Задача межпланетных путешествий разрешалась бы крайне просто. А если бы Земля вращалась еще быстрее, то мы сделались бы небесными странниками поневоле, так как инерция вращения сама отбросила бы нас в бездонную глубь неба. Людям приходилось бы задумываться уже над проблемой „земных", а не межзвездных странствований...
Но в силах ли мы заставить обитаемый нами земной шар вращаться быстрее, нежели теперь? Ведь это значит совершить нечто в роде чуда Иисуса Навина — приказать Солнцу изменить свой (кажущийся) дневной путь по небесному своду!
Многим читателям, без сомнения, приятно будет узнать, что теоретически это в нашей власти. При помощи довольно простого приема люди могли бы ускорить или, если угодно, замедлить вращение земного шара.
Придется, однако, начать несколько издалека, чтобы объяснить эту возможность.
Вам случалось, вероятно, замечать, что когда, спеша выйти на берег, вы идете по дну причалившей лодки, она, к немалой досаде вашей, сама отодвигается от берега. Этим неприятным сюрпризом вы обязаны тому закону механики, который называется „законом действия и противодействия". Закон состоит в том, что всякая действующая сила всегда вызывает равную силу противодействия. Что происходит, когда вы идете по дну лодки? Вы отталкиваете свое тело от опоры; вместе с тем отталкивается назад и сама опора. При ходьбе по неподвижному полу этого не замечается, так как отталкивающее усилие уничтожается сопротивлением неподвижной опоры [8].
Не заметите вы обратного перемещения и в том случае, когда лодка очень велика или тяжело нагружена: это потому, что одна и та же сила сообщает различным телам различное движение, в зависимости от их массы — тяжелое тело она перемещает с меньшею скоростью, нежели легкое. Переходя по палубе большого парохода от кормы к носу, вы также отталкиваете ногами все судно назад; но скорость этого перемещения, даже если бы ему не препятствовало трение о воду, была бы ничтожна: во столько же раз меньше скорости вашего собственного перемещения, во сколько раз пароход тяжелее вас самих. Но вернемся к нашей лодке. Представьте себе, что она имеет не удлиненную форму, а форму большой плавающей тарелки, и вообразите, что вы ходите кругом вдоль борта такой круглой лодки. Что при этом произойдет с ней? Догадаться не трудно: она придет во вращательное движение в обратном направлении, т. е., отталкиваясь ногами, вы, подобно лошади на топчаке, заставите ее вращаться. Проделав тот же маневр на палубе большого парохода, вы, конечно, не приведете его во вращение: масса такой громады слишком велика по сравнению с массой вашего тела; да и, кроме того, усилие ваших ног должно при этом преодолеть трение погруженной части судна о воду. И все же, теоретически рассуждая, некоторое перемещение достижимо: чем дольше вы будете кружиться по палубе, тем на больший угол повернется пароход. Возможно, что, сделав миллион кругов, вы повернете пароход на некоторую долю градуса... Чем значительнее груз, перемещаемый по палубе, тем большую силу затратите вы на его перемещение, а следовательно, тем сильнее будет и отталкивающее действие. Запрягши слонов в пушки и заставив их в течение многих суток кружиться по палубе, вы добились бы менее ничтожных результатов, чем кружась сами.
Вот небольшой приборчик (см. черт.), помощью которого можно наглядно иллюстрировать это отталкивающее действие движущегося тела на опору. Миниатюрный заводной паровозик бегает по кольцеобразным рельсам, укрепленным на легкоподвижном столике. И можно прямо видеть при этом, как весь столик сам вращается в обратную сторону.

Игрушечный паровозик, иллюстрирующий отталкивательное действие движущегося тела на опору: когда паровозик бежит по рельсам, подвижная платформа вращается в обратную сторону.
Мы подошли, наконец, вплотную к интересующему нас вопросу. Вообразите, что по экватору или по параллельным кругам Земли с востока на запад совершается непрерывное перемещение грузов: мчатся поезда, плывут пароходы, течет вода в каналах и т. д. — все в одном и том же направлении. Как отразится это на вращении Земли? После всего сказанного ответ ясен. Земля сама вращается с запада на восток; перемещение грузов на запад должно сообщить ей добавочное вращение в восточную сторону; следовательно, Земля будет вращаться быстрее. Значит, мы можем сократить продолжительность суток! Теоретически, как видите, это вполне в нашей власти; практически же осуществить это трудно по многим причинам, и прежде всего за недостатком времени. Масса тех паровозов, пароходов и той воды, которые будут перемещаться по земной поверхности, так мала по сравнению с колоссальной массой земного шара, что пройдут тысячи веков, прежде чем длина суток изменится на ничтожную долю секунды. А ведь нам нужно сократить сутки в 17 раз!
Впрочем, если бы выполнение подобного проекта и оказалось по силам человечеству, то, вращаясь столь быстро, земной шар под действием огромной центробежной силы расплющился бы в диск (в плоскости своего экватора), а, быть-может, даже еще ранее разлетелся бы на части, как черезчур быстро заверченный жернов[9].
Возможность путешествовать в межзвездных пространствах была бы приобретена слишком дорогой ценой...
VI.
Вопреки тяжести. — На волнах света.
Из трех мыслимых способов борьбы с тяготением мы рассмотрели и отвергли два: способ защиты от тяготения и способ ослабления земной тяжести. Мы убедились, что ни тот, ни другой не дают человечеству надежды успешно разрешить заманчивую проблему межпланетных полетов. Бесплодны всякие попытки укрыться от силы тяготения; безнадежно стремление ослабить напряжение тяжести. Остается одно: искать средство преодолеть тяготение и покинуть нашу планету вопреки ее притяжению.
Проектов подобного рода существует несколько. Для умов, практически настроенных, они, без сомнения, интереснее всяких других, так как их авторы не измышляют никаких фантастических веществ, в роде „экрана тяготения", не предлагают ни переделать земной шар, ни изменить скорость его вращения. Забегая вперед, я позволяю себе заинтриговать нетерпеливого читателя сообщением, что один из проектов типа: „вопреки тяжести" имеет шансы осуществиться в более или менее недалеком будущем.
Световое давление
Самый юный проект рассматриваемой категории предлагает воспользоваться для межпланетных перелетов давлением световых лучей. Лицам, мало знакомым с физикой, должно казаться невероятным, чтобы нежные, невесомые лучи света могли оказывать давление на озаряемые ими предметы. Между тем, одной из величайших заслуг безвременно скончавшегося гениального русского физика П. Н. Лебедева было то, что он доказал на опыте существование отталкивающей силы лучей света. Свет есть явление волнообразное, а всякая волнующаяся среда оказывает давление на встречаемую преграду.
В посмертной работе своей о световом давлении проф. П. Н. Лебедев писал:
„Давление волнующейся жидкости на препятствия, задерживающие распространение волн, легко наблюдать, если во время купания (в ванне или в пруде) ритмическим движением руки возбуждать волны и заставлять их отражаться от плавающего тела (бруска дерева): как только волны дойдут до бруска и начнут от него отражаться, так тотчас же брусок начинает двигаться с заметною скоростью в направлении распространения волн. Если на поверхности воды плавают мелкие предметы (например, опилки), которые волн не задерживают, то легко видеть, что волны двигают их вверх и вниз, но не увлекают с собою, и что, следовательно, движение плавающего тела обусловлено только силами падающих на него волн, а не движением самой жидкости".
Всякое светящееся тело — будь то свеча на вашем столе, электрическая лампа, раскаленное солнце или даже темное тело, испускающее невидимые лучи — давит своими лучами на озаряемые им тела. П. Н. Лебедеву удалось измерить силу давления, оказываемого солнечными лучами на освещаемые ими земные предметы: в мерах веса она составляет около ½ миллиграмма для площади в квадратный метр. Если умножить полмиллиграмма на число квадратных метров озаряемой Солнцем половины земного шара, мы получим весьма внушительный груз: 3½ миллиона пудов!
Такова величина силы, с которой Солнце давлением своих лучей постоянно отталкивает нашу планету. Взятая сама по себе, эта сила огромна; она подавляет воображение. Но в мире все относительно, и если сравнить ее с величиною солнечного притяжения, то окажется, что сила в 3½ миллиона пудов не может иметь ни малейшего влияния на движение земного шара, ибо она в 60 биллионов раз слабее силы солнечного притяжения! Далекий Сириус, от которого свет странствует к нам 10 лет, притягивает Землю с гораздо большею силою — 600 миллионов пудов — между тем планета наша словно не чувствует этого!
Однако, чем меньше тело, тем большую долю силы притяжения составляет сила светового давления. И вы поймете, почему это, если вспомните, что притяжение пропорционально массе тела, световое же давление пропорционально его поверхности. Уменьшите мысленно земной шар так, чтобы поперечник его стал вдвое меньше. Объем, а следовательно и масса Земли уменьшатся в 2 X 2 X 2 = 8 раз, поверхность же уменьшится лишь в 2 X 2 = 4 раза; притяжение ослабеет в 8 раз — пропорционально уменьшению массы; световое же давление уменьшится соответственно поверхности, т.-е. всего лишь в 4 раза. Вы видите, что притяжение ослабело более значительно, чем световое давление. Уменьшите Землю еще вдвое — получится снова выгода в пользу светового давления.
Если вы будете продолжать и далее такое уменьшение, т.-е. будете достаточно долго длить это неравное состязание кубов с квадратами, то неизбежно дойдете до таких мелких частиц, для которых световое давление, наконец, сравняется с притяжением. Подобная частица не будет уже притягиваться Солнцем — притяжение уничтожится равным отталкиванием. Вычислено, что для шарика плотности воды это должно иметь место в том случае, если поперечник его равен ½ миллионной доли миллиметра.
Солнечное притяжение и солнечное отталкивание
Легко понять, что если подобный шарик будет еще меньше, то сила светового отталкивания превзойдет силу притяжения — и крупинка будет уже стремиться не к Солнцу, а от Солнца. Чем меньше крупинка, тем сильнее должна она отталкиваться от Солнца. Перевес силы давления над тяготением, конечно, выражается ничтожной дробью, но и ничтожность — понятие относительное. Масса той пылинки, которую движет эта сила, также ведь чрезвычайно мала; и мы не должны удивляться тому, что маленькая сила весьма маленькой массе сообщает огромную окорость — десятки, сотни и тысячи верст в секунду... Читатель узнает ниже, что достаточно сообщить телу секундную скорость в десять верст, чтобы отослать его с земной поверхности в межпланетное пространство. Значит, если ничтожная земная пылинка очутится почему-либо за пределами атмосферы, она тотчас же будет подхвачена световым давлением и увлечется им в мировое пространство, навсегда покинув породившую ее Землю. „Она будет мчаться с возрастающей скоростью все далее и далее к окраинам нашей планетной системы, пересекая орбиты Марса, астероидов, Юпитера и т. д. При скорости 500 верст в секунду микроскопическая пылинка в одни сутки пролетит путь, равный поперечнику земной орбиты; а через две недели она будет уже у крайней границы солнечной системы.
Два американских ученых, Никольс и Гулл, изучавшие этот вопрос одновременно с П. Н. Лебедевым, произвели следующий чрезвычайно поучительный опыт. В абсолютно пустую стеклянную трубку, имеющую перехват, как в песочных часах, они насыпали смесь прокаленных грибных спор и наждачного порошка. Прокаленные и, следовательно, превращенные в уголь грибные споры необычайно малы и легки: они не более 0,002 миллиметра в поперечнике и в десять раз легче воды. Поэтому, если направить на них сильный свет, сосредоточенный помощью зажигательного стекла[10], то можно ожидать, что эти пылинки будут отталкиваться световыми лучами. Так действительно и происходило в опыте: когда смесь пересыпалась сквозь шейку перехвата, то направленный сюда свет (вольтовой дуги) отталкивал угольные пылинки, межу тем как более тяжелые частицы наждачного порошка падали отвесно.
Кометные хвосты
Загадочная особенность кометных хвостов, словно хвосты отталкиваемых Солнцем, по всей вероятности, объясняется именно лучевым давлением.
Об этом догадывался еще гениальный Кеплер, законодатель планетной системы, писавший три века тому назад следующие строки в своем трактате о кометах: „По натуре всех вещей полагаю, что, когда материя в пространство вселенной извержена бывает и сия пропускающая свет голова кометы прямыми лучами Солнца ударяется и пронизывается, то из внутренней материи кометы нечто им следует и тою же дорогою исходит, которой солнечные лучи пробивают и тело кометы освещают... Указание на причину, что из материи кометного тела нечто непрерывно изгоняется солнечными лучами силою оных, подал мне хвост кометы, о коем известно, что он всегда удаляется в сторону, противоположную Солнцу, и лучами Солнца формируется... Итак, нимало не сомневайся, читатель, что хвосты комет образуются Солнцем из материи, из головы изгнанной". Эти догадки Кеплера получили подтверждение (пока еще, впрочем, не окончательное) в работах последнего времени.
По способу мельчайших бактерий
Опыт, наглядно обнаруживающий давление световых лучей.
Легкие грибные споры в пустой трубке заметно отклоняются под давлением сосредоточенного пучка лучей, в то время как более тяжелые частицы наждачного порошка падают отвесно.
Опыт Никольса и Гулла
Лучи вольтовой дуги сосредоточиваются чечевицей в месте падения смеси грибных спор и наждачного порошка.
Доказано также, что отталкиваться лучами Солнца могут и микроскопические зародыши бактерий, если они очутятся в верхних, крайне разреженных слоях земной атмосферы.
Эти мельчайшие бактерии счастливее нас: они могут отдаваться увлекающему действию солнечных лучей и уноситься с невообразимой быстротой в безграничный простор вселенной...
Не может ли и человек воспользоваться тою же силою для межпланетных путешествий? Для этого не надо было бы непременно уменьшиться до микроскопических размеров — достаточно устроить снаряд с таким же выгодным отношением поверхности и массы, как у мельчайших пылинок, отталкиваемых лучами Солнца. Другими словами: озаряемая светом поверхность снаряда должна быть во столько же раз больше освещенной поверхности пылинки, во сколько раз вес снаряда больше веса этой пылинки.
Автор одного русского астрономического романа перенес своих героев на другие планеты именно в подобном снаряде. Его герои соорудили каюту из легчайшего материала, снабженную огромным, но легким зеркалом, которое можно было поворачивать на подобие паруса. Помещая зеркало под различными углами к солнечным лучам, пассажиры небесного корабля, смотря по желанию, либо ослабляли отталкивающее действие света, либо же совсем сводили его на нет, всецело отдаваясь притягательной силе. Они плавали взад и вперед по океану вселенной, посещая одну планету за другой.
Несбыточные надежды
В романе все это выходит правдоподобно и заманчиво. Но увы! Точный учет бесжалостно разрушает эту мечту, не оставляя и тени надежды на осуществление подобного проекта. Вычисление показывает, что зеркальная поверхность, площадью в один квадратный метр, должна весить всего миллиграмм, чтобы быть увлеченной в мировое пространство силою светового давления. До какой же неимоверной тонины нужно расплющить металл, чтобы квадратный метр его весил тысячную долю грамма! Даже для легчайшего металла, лития, это составило бы буквально толщину атома... Фантазия романиста пытается обойти это затруднение необоснованным допущением, что наука ошибается насчет истинной величины светового давления и что в действительности оно в тысячу раз более, чем мы полагаем. При таком допущении, — которое, к слову сказать, внесло бы изрядное расстройство в движение планет и особенно комет, — романисту (не без услужливой помощи крупной арифметической ошибки) удается соорудить межпланетный дирижабль, вполне пригодный для надобностей фантастического романа, но, к сожалению, совершенно неосуществимый в реальной действительности[11].
VII.
Из пушки на Луну. — Теория.
Небесные силы отказали нам в помощи. Остается расчитывать лишь на собственные силы, на могущество человеческой техники, преодолевшей уже не мало природных препятствий. Не найдем ли мы здесь достаточно могучего орудия, которое поможет нам разорвать оковы тяжести и ринуться в простор мироздания, чтобы исследовать иные миры?
Самая мощная машина
Надо было обладать оригинальным и смелым умом Жюля Верна, чтобы в смертоносном орудии — пушке — усмотреть средство вознестись живым на небо. Большинство людей не отдает себе отчета в том, что, с механической точки зрения пушка, — самая мощная из машин, созданных человеческой изобретательностью. Пороховые газы, образующиеся при выстреле в канале орудия, оказывают на снаряд давление в 2 — 3 тонны на квадр. сантиметр. Это в 2 — 3 раза превышает чудовищное давление водных масс в глубочайших пучинах океана. Чтобы оценить работоспособность современной пушки в единицах мощности, т. е. в лошадиных силах, рассмотрим 40-сантиметровое Крупповское орудие, выбрасывающее 40-пудовый снаряд (600 килограммов) с начальной скоростью 900 метров в секунду. „Живая сила" такого снаряда — полупроизведение массы на квадрат скорости — составляет около 24.000.000 килограммометров. Если принять во внимание, что такой огромный запас живой силы развивается в течение небольшой доли секунды — в данном случае 1/30, — то окажется, что секундная работа, выполняемая пушкой, то-есть ее мощность, определяется числом 10.000.000 лошадиных сил. Между тем мощность машин величайшего океанского парохода („Мажестик", 1922 г.) только 60.000 лош. сил; понадобилось бы около двухсот таких гигантских паровых двигателей, чтобы выполнить механическую работу, совершаемую пороховыми газами при каждом выстреле крупного орудия.
Мы видим, что не без основания французский романист предлагал именно с помощью пушки разрешить проблему заатмосферных полетов. В своих романах он оставил нам самый смелый и самый популярный проект межпланетных путешествий. Кто из нас в юности не путешествовал с его героями на Луну, поместившись внутри пушечного ядра?
Эта остроумная идея, разработанная покойным романистом в двух произведениях — „От Земли до Луны" и „Вокруг Луны", заслуживает гораздо большего внимания, чем то, которое обычно уделяется ей. Увлекшись фабулой романов, читатели склонны превратно оценивать их основную мысль, считая ее фантастичной там, где она вполне реальна, и, наоборот — реальной там, где она превращается в несбыточную мечту. Рассмотрим же поближе проект Жюля Верна, как чисто техническую идею, и постараемся выяснить, что в нем осуществимо и что относится к области несбыточного.
Признаюсь, не без волнения приступаю я к техническому разбору пленительных повестей симпатичнейшего из романистов. За полвека, протекшие со времени появления (1865 г.) этих увлекательных произведений, увенчанных французской академией, они успели стать любимым чтением молодежи всех стран. В годы моей юности они впервые зажгли во мне живой интерес к „царице наук" — астрономии; не сомневаюсь, что тем же обязаны им и многие тысячи других читателей. И если все же я решаюсь теперь вонзить анатомический нож в поэтическое создание романиста, то совесть мою успокаивает мысль, что я лишь следую примеру известного физика Шарля Гильома[12], даровитого соотечественника Жюля Верна.
Научное и ненаучное воображение
Вы имеете совершенно превратное представление о науке, если думаете, что она безжалостно подсекает крылья воображения и обрекает нас пресмыкаться в прозе и обыденности видимой действительности. Бесплодной Сахарой было бы поле научных исследований, если бы ученые не прибегали к услугам воображения, не умели отвлекаться от мира видимого, чтобы создавать мысленные, неосязаемые образы. Ни одного шага не делает наука без воображения; она постоянно питается плодами фантазии, но фантазии научной, рисующей воображаемые образы со всею возможною отчетливостью.
Научный разбор романа Жюля Верна не есть поэтому столкновение действительности с фантазией. Нет, это соперничество двух родов воображения — научного и ненаучного. И победа остается на стороне науки вовсе не потому, что романист слишком много фантазировал. Напротив, он фантазировал недостаточно, он не достроил до конца своих мысленных образов. Созданная им воображаемая картина межпланетного путешествия страдает неполнотой, недоделанностью. Нам придется восполнить эти недостающие подробности, и не наша вина, если упущенные детали существенно изменяют всю картину.
Надо ли пересказывать содержание романа, который у всех в памяти? Напомню лишь вкратце, словами самого Жюля Верна, главнейшие из интересующих нас обстоятельств.
Проект Жюля Верна
„В 186... году весь мир был в высшей степени взволнован одним научным опытом, первым и совершенно оргинальным в летописях науки. Члены Пушечного Клуба, основанного артиллеристами в Балтиморе после американской войны, вздумали вступить в сношение, с Луной, — да, с Луной, — послав на нее ядро. Их председатель, Барбикен, инициатор предприятия, посоветовавшись по этому поводу с астрономами Кэмбриджской [в Сев. Америке] обсерватории, принял все необходимые меры, чтобы обеспечить это необыкновенное предприятие.
„Согласно указаниям, данным членами обсерватории, пушка, из которой будет сделан выстрел, должна быть установлена в стране, расположенной между 0° и 28° северной или южной широты, чтобы можно было навести ее на Луну в зените. Ядру должна быть дана первоначальная скорость в 16 тысяч метров в секунду. Выпущенное 1-го декабря в десять часов сорок шесть минут сорок секунд вечера, оно должно достичь Луны через четыре дня после своего отправления, 5-го декабря ровно в полночь, в тот самый момент, когда она будет находиться в своем перигее, т.-е. в ближайшем расстоянии от Земли.
„Решено было, что: 1) ядро будет представлять собою алюминиевую гранату, диаметром в 108 дюймов, со стенками толщиною в двенадцать дюймов, и будет весить девятнадцать тысяч двести сорок фунтов; 2) пушка будет чугунная, длиною в девятьсот футов, и будет вылита прямо в земле; 3) на заряд будет взято четыреста тысяч фунтов пироксилина, который, развив под ядром шесть миллиардов литров газа, легко добросит его до ночного светила.
„Когда эти вопросы были разрешены, председатель клуба, Барбикен, выбрал место, где после чудовищной работы и была вполне успешно отлита эта колумбиада [пушка].
„В таком положении находились дела, когда случилось событие, во сто раз увеличившее интерес, возбужденный этим великим предприятием.
„Один француз, фантаст-парижанин, умный и отважный артист, попросил запереть его в ядро, так как он хочет попасть на Луну и познакомиться с земным спутником. "Он помирил председателя Барбикена с его смертельным врагом, капитаном Николем, и в залог этого примирения уговорил их отправиться вместе с ним в ядре. Предложение было принято. Изменили форму ядра. Теперь оно стало цилиндро-коническим. Этот род воздушного вагона снабдили сильными пружинами и легко разбивающимися перегородками, которые должны были ослабить силу толчка при выстреле. Захватили съестных припасов на год, воды на несколько месяцев, газа на несколько дней. Особый автоматический аппарат изготовлял и доставлял воздух, необходимый для дыхания трем путешественникам.
„1-го декабря в назначенный час, в присутствии необычайного скопления зрителей, начался полет, — и в первый раз три человеческих существа, покинув земной шар, понеслись в межпланетные пространства с полной уверенностью, что достигнут своей цели".
Можно ли перебросить ядро на Луну
Первый вопрос, который нам предстоит обсудить — это, конечно, вопрос о том, насколько допустима самая идея закинуть пушечное ядро на Луну. Многим кажется совершенно нелепой мысль о возможности бросить тело с такою скоростью, которая навсегда унесла бы его с Земли. Большинство людей привыкло думать, что всякое брошенное тело непременно должно упасть обратно. Таким людям фантастическая идея Жюля Верна о посылке ядра на Луну представляется совершенно беспочвенной. Мыслимо ли, в самом деле, сообщить земному телу такую скорость, чтобы оно не упало обратно на Землю, а безвозвратно покинуло бы нашу планету? Механика дает нам на этот вопрос вполне удовлетворительный ответ.
Предоставим здесь слово великому Ньютону. В своих „Математических началах физики", этом фундаменте величественного здания современной астрономии, он писал:

Пушка, стреляющая с воображаемой горы.
„Брошенный камень под действием тяжести отклоняется от прямолинейного пути и падает на Землю, описывая кривую линию. Если бросить камень с большей скоростью, то он полетит дальше; поэтому может случиться, что он опишет дугу в десять, сто, тысячу миль и, наконец, выйдет за пределы Земли и не вернется на нее больше. Пусть АВF (см. прилаг. рис.) представляет поверхность Земли С — ее центр, а — VD, VE, VF — кривые линии, которые описывает тело, брошенное в горизонтальном направлении с очень высокой горы с все большей и большей скоростью. Мы не принимаем во внимание противодействия атмосферы, т.— е. предполагаем, что она совершенно отсутствует. При меньшей первоначальной скорости тело описывает кривую VD, при большей скорости — кривую VE, при еще большей скорости — кривые VF, VG. Дри еще большей скорости тело обойдет вокруг всей Земли и возвратится к вершине горы, с которой его бросили. Так как при возвращении к исходному пункту скорость тела будет не меньше, чем в начале, то тело будет продолжать двигаться и дальше по той же кривой".
Теперь вам, без сомнения, понятно, что если бы на вершине этой воображаемой Ньютоновой горы помещалась пушка, то извергнутое ею ядро, при известной скорости и при отсутствии атмосферы, никогда не упало бы на Землю, а безостановочно кружилось бы вокруг нашей планеты, на подобие крошечной Луны. Мы можем даже в точности вычислить, какая начальная скорость нужна для такого полета ядра. Вычисление это настолько просто и результат настолько любопытен, что читатели, конечно, не откажутся произвести его сейчас вместе со мною.
Вычисление скорости

Вычисление начальной скорости ядра, которое никогда не должно упасть на Землю.
Чтобы найти искомую скорость, спросим себя сначала: почему всякое ядро, выброшенное пушкой горизонтально, в конце концов, падает на Землю? Потому что земное притяжение искривляет путь полета ядра — снаряд летит не по прямой линии, а по кривой, которая, в конце концов, упирается в земную поверхность. Легко понять, что если бы мы могли уменьшить кривизну пути ядра настолько, чтобы сделать ее одинаковой с кривизной шарообразной земной поверхности, то ядро наше никогда на Землю не упало бы, — оно вечно мчалось бы по кривой, концентрической с окружностью нашей планеты. Этого можно добиться, сообщив ядру достаточную скорость. Какую — мы сейчас определим. Взгляните на чертеж. Ядро, выброшенное пушкой из точки А по касательной, спустя одну секунду было бы, скажем, в точке В, — если бы не существовало земного притяжения. Тяжесть меняет дело, и под ее влиянием ядро через секунду окажется не в точке В, а ниже — настолько ниже, насколько всякое свободное тело опускается в первую секунду своего падения, именно — на 5 метров[13]. Если, опустившись на эти пять метров, ядро наше окажется выше уровня Земли ровно настолько же, насколько находилось оно и в точке А его исхода, то, значит, ядро летит как бы параллельно земной поверхности, не приближаясь и не удаляясь от нее. А это и есть то, чего мы желаем добиться. Нам остается теперь вычислить лишь длину АВ — т.-е. тот путь, какой должно было бы пройти ядро в одну секунду; результат и даст нам искомую секундную скорость ядра.
Знаменитая теорема Пифагора поможет нам вычислить этот отрезок АВ. В прямоугольном треугольнике АВО линия АО есть не что иное, как земной радиус, равный 6371000 метров. Отрезок ОС=АО, отрезок ВС = 5 метр., следовательно, OB=6371005 метр.
По теореме Пифагора имеем: 6371052=6371002 + АВ2.
Отсюда уже легко вычислить искомую величину скорости: АВ =7740 метров (около 7½ верст).
Итак, если бы пушка могла сообщить ядру начальную скорость 8 километров в секунду, то, при отсутствии атмосферы, такое ядро никогда уже не упало бы на Землю, а вечно обращалось бы вокруг земного шара. Пролетая в каждую секунду 8 килом., оно в течение 1 ч. 23 мин. уже описало бы полный круг в 40000 килом, и возвратилось в точку своего исхода, чтобы начать новый круг, и т. д. Это был бы настоящий спутник земного шара, наша вторая Луна, более близкая и более быстрая, чем первая. Ее „месяц" равнялся бы всего только 1 часу 23 минутам. Она мчалась бы в 17 раз быстрее, чем любая точка земного экватора, и если вы вспомните то, что сказано было нами выше об ослаблении тяжести вследствие вращения Земли (см. стр. 35), то вам станет вполне ясно, почему наше ядро не падает на Землю. Ведь мы знаем уже, что если бы земной шар вращался в 17 раз быстрее, то тела на экваторе потеряли бы целиком свой вес; скорость же нашего ядра — 8 килом, в секунду — именно в 17 раз больше скорости точек земного экватора.
Как видите, мы могли бы и сразу, без всяких геометрических построений и выкладок, найти интересующую нас скорость ядра: для этого достаточно было бы просто увеличить в 17 раз скорость движения точек земного экватора. Надеюсь, читатель не посетует на меня за то, что я провел его окольной дорогой, с тайным умыслом дать некоторое представление о простейших расчетах в механике...
Человеческой гордости должно льстить сознание, что мы имеем возможность — пока, правда, лишь теоретическую — подарить Земле хоть и маленького, но все же настоящего спутника. Пылкий герой Жюль-Вернова „Путешествия на Луну" Дж. Мастон не без основания воскликнул, что в создании пушечного ядра человек, по силе своего могущества, наиболее приблизился к богу: „Как бог создал звезды и планеты, так человек создал ядро, это подобие несущихся в пространстве светил, которые, в сущности, те же ядра". Еще справедливее это для того ядра, которое человек может закинуть в мировое пространство. Это новое небесное тело, при всей своей миниатюрности, будет нисколько не хуже всех остальных. Оно строго подчинится трем законам Кеплера, управляющим движениями планет и их спутников.
Нужды нет, что пушечное ядро — предмет „земной": очутившись в мировом пространстве, он превращается в настоящее небесное тело. В удрученном кошмаром мозгу Ивана Карамазова промелькнула совершенно правильная мысль, что и простой топор в мировом пространстве становится космическим телом и подчиняется законам небесной механики:
„Что станется в пространстве с топором?.. Если куда попадет подальше, то примется, я думаю, летать вокруг Земли, сам не зная зачем, в виде спутника. Астрономы вычислят восхождение и захождение топора, Гатцук внесет в календарь, вот и все".
Искусственная Луна
Мы можем, если хотите, тут же устроить краткий экзамен нашему пушечному ядру, "выступающему в роли небесного тела. Проверим, подчиняется ли оно, например, третьему закону Кеплера, гласящему: „Квадраты времен обращения небесных тел относятся между собой, как кубы их средних расстояний от общего центра притяжения". Для подобной проверки мы должны приложить этот закон к Луне и к нашему пушечному ядру, как к двум телам, обращающимся вокруг земного шара. Луна совершает полный оборот вокруг Земли в 27⅓ суток, или в 656 часов, и находится на расстоянии 60 земных радиусов от центра Земли. Пушечное ядро делает полный оборот всего в 1½ часа и находится от земного центра в расстоянии одного земного радиуса. Для торжества закона Кеплера требуется, чтобы для обоих небесных тел существовало такое соотношение:

Если дадите себе труд проделать это вычисление, вы убедитесь, что равенство отношений получается довольно близкое (надо считаться с тем, что числа этой пропорции, ради простоты, закруглены, так что полной точности ожидать нельзя).
Итак, сообщив пушечному ядру начальную скорость 8 килом, в секунду, мы превращаем его в маленькие небесное тело, которое, побеждая силу притяжения, уже не возвращается на Землю[14]. Что же будет, если мы сообщим ядру еще большую начальную скорость? В небесной механике доказывается, что при начальной секундной скорости в 8, в 9, в 10 килом, ядро, горизонтально выброшенное пушкой, будет описывать вокруг Земли не окружность, а эллипс — тем более вытянутый, чем значительнее начальная скорость.

По каким путям направились бы пушечные ядра, если бы можно былобросать их с Земли с весьма большими скоростями
Когда же мы доведем эту скорость приблизительно до 11 килом., то эллипс превратится уже в незамкнутую кривую, — в параболу. Точнее говоря, он должен был бы превратиться в параболу, если бы Земля была единственным телом, притяжение которого влияет на путь нашего ядра. Могучее притягательное действие Солнца существенно усложнит путь ядра, — но, во всяком случае, при указанной начальной скорости, 11 килом., ядро навсегда удалится от Земли. Если оно будет при этом брошено в надлежащем направлении, то избегнет падения на Солнце и будет вечно обращаться вокруг него, подобно земному шару и другим планетам. В астрономическом смысле оно повысится в ранге: из спутника Земли превратится в спутника Солнца, в самостоятельную планету. Человечество подарит вселенной новое миниатюрное небесное тело.

Судьба ядер, выброшенных пушкой с весьма большой скоростью.
Ради простоты, мы начали с рассмотрения горизонтально брошенного тела. В небесной механике доказывается, однако, что те же выводы справедливы и для тела, брошенного под углом к горизонту или даже вертикально, как ядро в романе Жюля Верна. Во всех случаях, при достаточной скорости, брошенное тело навсегда покидает Землю и уносится в пустыни мирового пространства.
Вот какие чудесные возможности открывает перед нами теория. Но что же говорит ее несговорчивая сестра — практика? В состоянии ли современная артиллерия осуществить эти возможности?
К сожалению, пока еще нет. Самые могучие из наших пушек не в силах пока сообщить своим ядрам таких огромных скоростей. Снаряды современной самой дальнобойной пушки[15] покидают жерло с начальной скоростью, достигающей 1½ верст. Это втрое быстрее, чем движение точек земного экватора, но в пять раз медленнее, чем нужно, чтобы бросить ядро на Луну.
Метательные орудия прежде и ныне
Однако, не будем терять надежды. Переход от 1 к 5 не так уж значителен. Техника в своем победном шествии оставила за собою гораздо большую пропасть, когда заменила жалкие катапульты древних мощными орудиями современной артиллерии. Римские легионеры назвали бы безумцем всякого, кто сказал бы им, что их потомки будут перебрасывать 60-пудовые ядра на расстояние 30-ти и более верст. Едва ли даже Жюль Верн мог думать, что через полвека 16-дюймовые крепостные и морские орудия будут извергать снаряды в 65 пудов на расстояние 37-ми верст, а германцы — обстреливать Париж в 1917 г. почти с 80-верстного расстояния!.. Энергия, выбрасывающая снаряд из крупного орудия, превышает энергию человека, бросающего камень невооруженной рукой, в десять миллионов раз. Если мы могли так головокружительно далеко превзойти силу первобытного дикаря, то можно ли ставить какие — нибудь границы дальнейшему росту могущества техники?
Нет ничего невозможного в том, что Шварц или Нобель недалекого будущего изобретет орудие, которое по силе извержения настолько же превзойдет современную пушку, насколько последняя превосходит катапульту древних римлян...
На Луне, где напряжение тяжести вшестеро слабее, чем на Земле, и где совершенно отсутствует атмосфера, служащая серьезным препятствием полету ядра, — там для осуществления горделивого замысла героев Жюля Верна вполне достаточна была бы одна из тех чудовищных пушек, которыми мы уже располагаем в данный момент[16].
А на спутнике Марса — на крошечном Фобосе — достаточно было бы просто бросить камень рукой, чтобы он никогда уже не упал обратно. По поверхности такого миниатюрного мира (не более 10 верст в поперечнике) опасно кататься в автомобиле или на велосипеде; развив даже умеренную скорость, седоки вместе с их машинами рискуют взлететь вверх, умчаться с мировое пространство и превратиться в самостоятельные небесные тела...
Но мы живем не на Фобосе и не на Луне, а на Земле. Нам необходимо поэтому добиваться секундной скорости в восемь и более верст, чтобы иметь возможность перекидывать пушечные ядра на иные планеты.
VIII.
Из пушки на Луну. — Практика.
Мы проследили за тем ходом мыслей, который привел Жюля Верна к идее перебросить ядро на Луну. Если бы вопрос состоял только в этом, если бы мы искали лишь способа установить между планетами своего рода небесную почту, отправлять в далекие миры посылки для неведомых адресатов, — то задача решалась бы проектом Жюля Верна довольно удовлетворительно. (Конечно, оставалось бы еще преодолеть сопротивление атмосферы, которое гораздо значительнее, чем мы представляем себе; но об этом речь будет впереди).
До сих пор мы заботились только о ядре, о том, чтобы оно полетело достаточно быстро и чтобы достигло своей цели. Мы совсем не думали о том, что будет происходить внутри ядра. А ведь наше ядро — не простой артиллерийский снаряд; это ядро-вагон, в котором находятся живые существа, пассажиры. Какая же участь ожидает их при полете?
Вот здесь-то, а вовсе не в самой мысли перекинуть ядро на Луну, надо искать Ахиллесову пяту заманчивого проекта Жюля Верна.
Внутри ядра
Это небывалое путешествие пройдет для пассажиров Жюль-Вернова ядра далеко не так мирно и благополучно, как описано в романе. Не думайте, однако, что опасность грозит им во время путешествия от Земли до Луны. Ничуть! Если бы им удалось остаться живыми к моменту, когда они покинут канал пушки, то во все время дальнейшего путешествия им нечего уже было бы опасаться. В океане вселенной нет ни бурь, ни волн, ни качки. А огромная скорость, с которой пассажиры летели бы в мировом пространстве вместе с их вагоном, была бы столь же безвредна для них, как безвредна для нас, обитателей Земли, та 30-верстная быстрота, с какой планета наша мчится вокруг Солнца.
Первый удар
Опасный момент для Жюль-Верновых путешественников представляют те несколько сотых долей секунды, в течение которых ядро-каюта будет двигаться в канале самой пушки. Ведь в течение этого ничтожно малого промежутка времени скорость движения пассажиров должна неимоверно возрасти: от нуля до 16 килом.[17]. Герои романа были вполне правы, утверждая, что момент, когда ядро полетит, будет столь же опасен для пассажиров, как если бы они находились не внутри ядра, а прямо перед ним. Действительно, в момент выстрела нижняя площадка (пол) каюты должна ударить пассажиров с такой же силой, с какой обрушилось бы ядро на всякое тело, находящееся снаружи его. Пассажиры отнеслись к этой опасности черезчур легко, если воображали, что отделаются лишь сильным приливом крови к голове. Дело обстоит неизмеримо серьезнее. Нам станет ясно это, когда произведем несколько несложных расчетов. В канале пушки ядро движется ускоренно, т.-е. скорость его увеличивается под постоянным напором газов, образующихся при взрыве; в течение ничтожной доли секунды она возрастает от нуля до 16 килом. Как же велико „ускорение" этого стремительно ускоряющегося движения? Другими словами: на какую величину нарастает здесь скорость в течение секунды? Нужды нет, что все движение длится лишь малую долю секунды: мы можем вести расчет на целые секунды (определяем же мы годовой доход по месячному заработку). И вот оказывается[18], что секундное „ускорение" ядра, скользящего в канале орудия, выражается огромной цифрой — 640 килом. Для сравнения замечу, что секундное ускорение трогающегося курьерского поезда равно одному аршину...
Раздавлены собственным весом
Но все значение для пассажиров ядра этой цифры — 640 килом. в секунду — мы отчетливо постигнем лишь тогда, когда сравним ее с обычным весом ускорением падающего тела на земной поверхности; оно равно всего лишь 10 метрам, т.-е. в 64.000 раз меньше! Значит, внутри снаряда всякий предмет в момент выстрела придавливался бы ко дну ядра с силой, которая в 64.000 раз больше веса самого предмета! Другими словами: пассажиры почувствовали бы, что внезапно сделались в десятки тысяч раз тяжелее. Неизменный цилиндр мистера Барбикена один весил бы тысячу пудов! Правда, это длилось бы всего мгновение — 40-ю долю секунды, — но можно не сомневаться, что под действием такой колоссальной тяжести люди были бы буквально расплющены.
Правда, герои Жюля Верна приняли меры для ослабления силы удара: ядро снабжено было пружинными буферами и двойным дном с водой, заполняющей пространство между ними. От этого продолжительность удара немного растягивается, и, следовательно, быстрота нарастания скорости ослабляется. Но при тех огромных величинах, с которыми приходится иметь здесь дело, выгода получается черезчур мизерная: сила, которая должна придавливать пассажиров к полу, уменьшается на какую-нибудь сотую долю, не более.
Сопротивление воздуха
И это еще не все, что ожидает пассажиров в течение того краткого мига, который они проведут в канале пушки. Если бы каким-нибудь чудом они остались живы в момент взрыва, гибель ожидала бы их у выхода из орудия. Вспомним о сопротивлении воздуха! При обычных условиях мы мало думаем о том, чтобы такая легкая среда, как воздух, могла серьезно мешать движению тела. Но это только потому, что обычные скорости сравнительно невелики. С возрастанием скорости, сопротивление воздуха быстро увеличивается. Велосипедисты и автомобилисты по собственному опыту знают, какой помехой является воздух. Сопротивление воздуха возрастает гораздо быстрее, чем скорость[19], и для весьма быстро летящих тел — например, для падающих метеоритов (до 75 килом. в сек.) — воздух становится как бы броней: метеориты большею частью сгорают или рассыпаются в пыль еще в высоких, крайне разреженных, слоях атмосферы.
Еще удар
Вы понимаете теперь, что ядро, покидающее Жюль-Вернову пушку с пятнадцативерстной скоростью, должно встретить со стороны воздуха неимоверное сопротивление, — едва ли не такое же, как от твердого тела. Ведь оно мчится раз в 20 быстрее наших современных ядер! Воздух действовал бы на него, как толстая броня... Движение ядра мгновенно замедлилось бы; может-быть, даже разорвалась бы пушка, как бы закупоренная своим ядром. Но пассажиры внутри ядра продолжали бы двигаться по инерции с пятнадцативерстной секундной скоростью. С чудовищной силой ударились бы они о потолок своей каюты и, если бы сохранили жизнь при отправлении ядра в путь, то неминуемо погибли бы при этом втором ударе. Ведь даже при умеренной скорости трамвая мы падаем на пол, если неопытный вагоновожатый слишком резко останавливает вагон. А ядро Жюля Верна неслось в пять тысяч раз быстрее трамвая[20]...
От этого удара, вызванного сопротивлением атмосферы, мы могли бы избавить пассажиров разве лишь в том случае, если бы ухитрились поместить пушку так высоко, чтобы жерло ее находилось уже за пределами плотной части атмосферы.
Но как избегнуть первого удара, — сотрясения при взрыве и сопровождающей его роковой быстроты нарастания скорости?
Средства избегнуть сотрясения
Этого можно было бы достигнуть весьма значительным удлинением канала пушки. Легко убедиться вычислением (см. прибавление 6-е в конце книги), что если, например, мы хотим, чтобы „искусственная" тяжесть внутри ядра в момент выстрела равнялась обыкновенной тяжести на земном шаре, нам нужно изготовить пушку длиною, ни мало, ни много — в 6.000 килом. Жюль-Вернова колумбиада должна была бы простираться в глубь земного шара до самого его центра, чтобы пассажиры действительно были избавлены от всяких неприятностей: к их обычному весу присоединится тогда только незначительный „искусственный" вес вследствие постепенного нарастания скорости, и они почувствовали бы, что стали всего вдвое тяжелее.
Надо заметить, что человеческий организм в течение краткого промежутка времени без вреда переносит увеличение собственной тяжести в несколько раз. Когда мы скатываемся с ледяной горы вниз и здесь быстро меняем направление своего движения, то вес наш в этот краткий миг увеличивается в 10 — 20 раз (т.-е. тело наше в несколько десятков раз сильнее обычного прижимается к салазкам). Если допустить, что человек может безвредно переносить в течение короткого времени 20-кратное увеличение своего веса, то для отправления людей на Луну достаточно будет отлить пушку в 300 килом. длиною. Однако, и это мало утешительно, потому что подобное сооружение лежит за пределами технического достижения. Не говорю уже о том, что извергающая сила такой непомерно длинной пушки должна значительно уменьшиться вследствие трения ядра в 300-верстном канале орудия.
Физика указывает и на другое средство ослабить силу удара. Самую хрупкую вещь можно уберечь от поломки при сотрясении, если погрузить ее в жидкость равного удельного веса. Так, если заключить хрупкий предмет в сосуд с жидкостью такой же плотности и герметически закупорить его, то подобный сосуд можно ронять с высоты и вообще подвергать сильнейшим сотрясениям (при условии, разумеется, что сосуд остается целым), — и хрупкий предмет от толчков почти не страдает. Мы могли бы поэтому осуществить смелую затею Жюль-Верновых артиллеристов, если бы наполнили внутренность ядра соленой водой, по плотности равной плотности человеческого тела, и в эту жидкость погрузили пассажиров, одетых в водолазные костюмы, с запасом воздуха. После выстрела, когда нарастание скорости прекратится и пассажиры приобретут скорость ядра, они могли бы уже выпустить воду и устроиться в каюте, не опасаясь никаких неприятных неожиданностей. Их ожидали бы, правда, удивительные, но вполне невинные сюрпризы, которых Жюль Берн совершенно не предусмотрел — однако, об этом мы побеседуем позднее.
Итак, вот какие серьезные затруднения нужно было бы преодолеть, чтобы в действительности осуществить заманчивый проект Жюля Верна:
1) Изобрести взрывчатое вещество значительно сильнее ныне употребляемых, или придумать какой-нибудь другой способ метать весомые тела со скоростью, впятеро большей, чем начальная скорость современных ядер и пуль.
2) Соорудить пушку длиною в 300 верст, или же герметически закупорить пассажиров в водяную ванну.
3) Поместить пушку так, чтобы жерло ее выступало за пределы земной атмосферы.
Безотрадные выводы
И в результате — отправиться в небесное странствование без всякой надежды вернуться не только живым, но даже и мертвым: ведь лишь счастливая случайность дала возможность героям романа возвратиться на Землю. Жюль-Верново ядро — снаряд неуправляемый, и чтобы дать ему новое направление, надо зарядить им пушку. А где ее взять в мировом пространстве или на другой планете? Пассажирам придется навеки проститься с родной Землей, с земным человечеством.
Невольно вспоминается глубокое изречение Паскаля: „Никто не странствовал бы по свету, если бы не надеялся когда-нибудь рассказать другим о том, что видел"... А именно этой надежды пушка Жюля Верна нам не оставляет.
IX.
К звездам на ракете.
После многих разочарований мы подходим, наконец, к единственному, действительно осуществимому проекту межпланетных путешествий — осуществимому не сегодня, но в более или менее близком будущем. Этот прожект разработан русским ученым К. Э. Циолковским и стоит в стороне от всех фантастических замыслов, рассмотренных ранее. Здесь перед нами уже не фантазия романиста, не любопытная задача из области небесной механики, — а глубоко продуманная техническая идея, высказанная вполне серьезно. Она указывает нам на единственный реальный путь к осуществлению заатмосферных полетов в управляемом снаряде.
Третий закон Ньютона
Ничто не может быть проще той мысли, которая положена в основу этого проекта — двигаться в пустых пространствах без всякой опоры. На первых же уроках физики мы узнаем закон „действия и противодействия" или „третий закон Ньютона": сила действующая всегда вызывает равную силу противодействия. Эта-то сила и поможет нам умчаться в бездны мироздания. Сила противодействия проявляется на каждом шагу, — быть-может, именно потому мы и не отдаем себе ясного отчета в ее существовании; нужны особые обстоятельства, чтобы заставить нашу мысль остановиться на ней.
Когда вы стреляете из ружья, вы чувствуете его „отдачу": давление взрывных газов отбрасывает пулю в одну сторону и с точно такою же силою отталкивает ружье в обратную сторону. Если бы ружье весило столько же, сколько и пуля, то приклад ударил бы стреляющего так же сильно, как ударяет пуля, выпущенная в упор; каждый стрелок был бы тогда самоубийцей. Но ружье значительно тяжелее пули, — и во столько же раз ослабляется действие его возвратного удара. Ведь действие силы на тело зависит от массы этого тела: одна и та же сила сообщает грузному телу меньшую скорость, чем легкому (соответственно отношению их масс). Закон „равенства действия и противодействия" не следует поэтому понимать буквально, — ибо действие почти никогда не равно противодействию, а равны лишь действующие при этом силы, могущие вызвать весьма различные результаты.
При падении яблока на Землю не думайте, что земной шар остается неподвижным, нарушая закон „действия и противодействия"; притяжение и здесь взаимное: сила действия Земли на яблоко вызывает точно такую же силу противодействия. Яблоко и Земля, в сущности, падают друг на друга, влекомые равными силами; но так как масса земного шара неизмеримо больше массы яблока, то скорость „падения" Земли неизмеримо меньше скорости падения яблока. Практически Земля остается неподвижной, и наблюдается лишь движение яблока.
Движение возвратным ударом
Этот-то закон, впервые провозглашенный великим Ньютоном, открывает перед нами возможность свободно двигаться, ни на что не опираясь. Перемещаться, ни от чего не отталкиваясь, одними лишь внутренними силами — это звучит так, словно речь идет о поднятии самого себя за волосы, по анекдотическому способу барона Мюнхгаузена. Но сходство — чисто внешнее. По существу же здесь огромная разница, и насколько бесполезно поднимать себя за волосы, настолько действителен способ движения по принципу возвратного удара, т.-е. отдачи. Природа давно уже осуществила этот способ перемещения для многих живых существ. Каракатица движется так: она набирает воду в жаберную полость и затем энергично выбрасывает струю воды через особую воронку впереди тела; вода устремляется вперед, а сама каракатица получает обратный толчок, отбрасывающий ее назад: направив трубку воронки вбок или назад, животное может таким своеобразным способом двигаться в любом направлении. Подобным же образом перемещают свое тело медузы, сальпы, личинки стрекоз и многие другие обитатели вод.
Пользуется этим приемом и человеческая техника: вращение водяных и некоторых паровых турбин также основано на законе равенства действия и противодействия.
Нигде, однако, интересующий нас способ перемещения не проявляется так наглядно, как при полете обыкновенной ракеты. Сколько раз любовались вы эффектным взлетом ракеты, но едва ли приходило вам в голову, что вы видите перед собой уменьшенное подобие будущего межзвездного дирижабля...
Полет ракеты
Отчего ракета взлетает вверх при горении наполняющего ее пороха? Даже среди людей науки приходится нередко слышать, будто ракета летит вверх потому, что газами, которые образуются при горении пороха внутри ее, она „отталкивается от воздуха". Однако, если пустить ракету в безвоздушном пространстве, она полетит нисколько не хуже, даже лучше, чем в воздухе. Истинная причина движения ракеты состоит в том, что, когда пороховые газы стремительно вытекают из нее вниз, сама трубка ракеты, по закону действия и противодействия, отталкивается вверх. Здесь происходит то же, что и при выстреле из пушки: ядро летит вперед, пушка отталкивается назад. Если бы пушка висела в воздухе, ни на что не опираясь, она после выстрела двигалась бы назад со скоростью, которая во столько раз меньше скорости ядра, во сколько ядро легче пушки. Ракета выбрасывает не ядро, а газообразные продукты взрыва; скорость и масса этих газов так значительны, что „отдача" ракеты заставляет ее быстро взлетать вверх. Пока происходит горение пороха, скорость ракеты все возрастает, ибо к прежней скорости непрерывно прибавляется новая, да и сама ракета, теряя свои горючие запасы, становится легче. Когда же порох весь выгорит, пустая ракетная трубка, пролетев еще немного по инерции, падает обратно на землю: ее скорость недостаточна для окончательного преодоления силы тяжести.
Но вообразите ракету размерами в несколько сажен, снабдите ее большим запасом сильнейшего взрывчатого вещества, чтобы она приобрела секундную скорость около 11 килом, (такая скорость, как мы знаем, достаточна, чтобы безвозвратно покинуть Землю) — тогда цепи земного тяготения будут разорваны. Способ странствовать в мировом пространстве найден!
Вот соображения, приводящие к мысли об устройстве летательного аппарата, способного двигаться не только в атмосфере, но и за ее пределами. Впервые мысль о подобном аппарате — правда, для земных, а не для межпланетных полетов — была высказана в 1881 г. известным русским революционером-ученым Н. И. Кибальчичем в проекте, составленном этим замечательным человеком незадолго до казни. В течение 36 лет проект Кибальчича оставался погребенным в архивах русского департамента полиции, и лишь в 1918 г., когда проект был, наконец, опубликован, стало известно, что знаменитый революционер мечтал о летательном снаряде, построенном по типу ракеты.
Проект Кибальчича был высказан им лишь в форме основной идеи: „Будучи на свободе, я не имел достаточно времени, чтобы разработать свой проект в подробностях и доказать его осуществимость математическими вычислениями", — писал он[21]. Гораздо полнее и обстоятельнее разработана та же мысль другим русским ученым, физиком К. Э. Циолковским, создавшим — независимо от Кибальчича — проект настоящего межпланетного дирижабля.
Проект К. Э. Циолковского
Снаряд К. Э. Циолковского — не что иное, как огромная ракета с особой каютой для пассажиров, для хранения съестных продуктов, запасов сгущенного воздуха, научных приборов и прочего. Люди в таком снаряде — изобретатель заранее окрестил его „Ракетой" — будут при помощи особого механизма направлять истечение газов в любую сторону. Это будет настоящий управляемый космический корабль, на котором можно уплыть в беспредельное мировое пространство, полететь на Луну, на планеты, к звездам... Пассажиры могут посредством многих отдельных мелких взрывов увеличивать скорость этого межпланетного дирижабля с необходимой постепенностью, чтобы возрастание ее было безвредно для них.
При желании спуститься на какую-нибудь планету, они могут, такими же взрывами, уменьшить скорость снаряда и тем ослабить силу падения. Наконец, пассажиры могут тем же путем возвратиться и обратно на Землю. Для всего этого надо только захватить с собою достаточный запас взрывчатых веществ.
Заметьте существенные преимущества, которыми обладает „Ракета" К. Э. Циолковского по сравнению с пушечным ядром Жюля Верна. Ракета развивает свою чудовищную скорость не сразу, как пушечное ядро, а постепенно, избавляя пассажиров от опасности быть раздавленными стремительным возрастанием их собственного веса.
Не опасно для „Ракеты" и сопротивление воздуха: она может прорезать атмосферу не со столь большой скоростью и, лишь очутившись высоко над землей, за пределами воздушной оболочки, развить полную „межпланетную" скорость. А затем в мировом просторе работа двигателя (т.-е. истечение газов) может быть совершенно прекращена: „Ракета" будет лететь по инерции со скоростью, которая была достигнута в последний момент. Она может мчаться так, без малейшей затраты взрывчатого вещества, миллионы и биллионы верст, лететь недели, месяцы, целые годы. Лишь для перемены направления полета или для ослабления удара при спуске на планету понадобится снова пустить в действие взрывной аппарат. Затрата взрывчатого вещества, как видите, вовсе не будет здесь безмерно огромна.
Но самое главное преимущество „Ракеты" состоит в том, что она даст будущим морякам вселенной полную возможность, посетив какую-либо планету, в желаемый момент снова возвратиться на родную Землю. Нужно лишь обильно запастись взрывчатыми веществами, как полярные путешественники запасаются топливом.
Здесь неуместно входить в технические подробности. Вопрос интересует нас лишь с точки зрения физики неба. Предоставим инженерам разбираться в технической стороне дела[22]. Для нас важно было лишь установить тот механический принцип, на котором основано устройство межпланетного корабля типа „Ракеты", и который остается неизменным, как бы ни варьировалась конструкция аппарата.
Что мешает теперь же осуществить этот грандиозный замысел?
Не сегодня – завтра
Главное, пожалуй, даже единственное препятствие к немедленному осуществлению реактивного небесного дирижабля — это отсутствие достаточно сильного взрывчатого вещества. Мы не знаем источника, который при современном состоянии техники способен был бы развить силу, достаточную для движения огромной ракеты. Но вспомним, что в таком же положении были недавно и первые пионеры авиации: принцип летания по способу парения был указан правильно, и остановка была тоже лишь за достаточно могучим двигателем. Всего 20 лет отделяет нас от того времени, когда аэроплан был только красивым проектом, неосуществимым за недостатком могучего двигателя. Всего 12 лет прошло с тех пор, как в России взвился первый аэроплан. А теперь тысячесильные исполинские самолеты уже переносят сотню людей через материки и океаны. Мы в праве поэтому надеяться, что если не сегодня, то завтра будет найден необходимый источник энергии также и для небесных кораблей.
Тогда заманчивая мечта о достижении иных миров, о путешествии на Луну, на Марс или Сатурн, превратится, наконец, в реальную действительность. Воздух для дыхания нетрудно будет взять с собой (в виде хотя бы сжатого кислорода), как и аппараты для поглощения выдыхаемой углекислоты. Вполне мыслимо также снабдить небесных путешественников достаточным запасом пищи, питья и т. п. С этой стороны не предвидится никаких серьезных препятствий для путешествия, например, на Луну, а со временем и на планеты.
Достижение иных миров
Спуск на планету — если только поверхность ее в таком состоянии, что делает спуск возможным — будет лишь вопросом достаточного количества взрывчатых веществ. Надлежаще направленными взрывами можно уменьшить огромную скорость снаряда настолько, чтобы падение его совершилось плавно и безопасно. И надо иметь еще в запасе достаточно взрывчатого вещества, чтобы вновь покинуть это временное пристанище, преодолеть силу притяжения планеты и пуститься в обратный путь.
В особых непроницаемых костюмах, в роде водолазных, будущие Колумбы вселенной, достигнув планеты, смогут рискнуть выйти из небесного корабля. С запасом кислорода в металлическом ранце за плечами будут они бродить по почве неведомого мира, делать научные наблюдения, изучать его природу, мертвую и живую (если такая имеется), собирать коллекции... А более далекие экскурсии они смогут совершать в наглухо закрытых автомобилях, привезенных с собой. С технической стороны для всего этого едва ли могут представиться затруднения, раз люди сумели проникнуть даже глубоко в воды океана и изучать его пучины, казалось бы, навсегда недоступные для смертного[23]...
Остановимся теперь на вопросе о продолжительности небесных перелетов.
Продолжительность небесных перелетов
Сколько времени будет длиться перелет на Луну? Не свыше двух суток, т.-е. меньше, чем из Петрограда в Одессу. Но Луна — самая близкая из небесных станций на пути в бесконечность. Чтобы достигнуть следующей станции, Венеры, потребуется уже целый месяц. Путешествие на Марс или на Меркурий продлится около двух месяцев. И все это при наименьшей из возможных скоростей — при 40 верстах в секунду[24]. Цифры внушительные, — но давно ли мы ездили из Петрограда во Владивосток, целый месяц не выходя из вагона? А Магеллан во время своего двухлетнего путешествия плавал по Тихому океану четыре месяца, нигде не встречая обитаемой земли...
Для достижения орбиты Юпитера понадобится непрерывно лететь в мировом пространстве с 40-верстной скоростью около полугода. Года два отнимет путешествие к загадочному миру Сатурна; четыре года займет небесное странствование к орбите Урана. И, наконец, чтобы достичь самой крайней из известных нам планет солнечной системы, придется затратить „не более" 5 — 6 лет жизни.
А дальше?
Межзвездные пустыни
Дальше, за границами нашего планетного царства, на многие миллионы миллионов верст расстилается межзвездная пустыня. Звезда от звезды, солнце от солнца отделены во вселенной такими безднами пространств, каких не в силах представить самое пылкое воображение. Ум не охватывает столь огромных расстояний. Вообразим, что вселенная уменьшилась в своих размерах, и пусть вся солнечная система, ограниченная орбитой далекого Нептуна, как-раз покрывает арену Московского цирка. Тогда, на плане такого масштаба, не только вся Москва с ее окрестностями и вся Московская губерния были бы совершенно свободны от звезд, но даже через все прилегающие губернии простиралась бы еще пустыня без единой звезды. И лишь на расстоянии Петрограда мы встретили бы первую, ближайшую звезду — Альфу Центавра, окруженную такою же бездною пустынь! На всем пространстве Европейской России мы едва насчитали бы полдюжины звезд (яркий Сириус оказался бы в их числе). Остальных из „ближайших" соседок нашего солнца не могла бы вместить ни Европа, ни даже весь материк Старого Света. Яркую Капеллу пришлось бы поместить к антиподам, в Америку, а звезду Канопус — вне Земли, в мировом пространстве, приблизительно на расстоянии Луны!
Так необъятны пустыни звездного мира...
Световой луч, скорость которого столь велика, что обычно мы считаем распространение света на Земле мгновенным, странствует до ближайших звезд целые годы, десятки лет. А ведь свет пронизывает пространство в тысячи раз быстрее, чем должен мчаться межпланетный дирижабль будущего. Значит, целые тысячелетия потребуются для перелета в системы других звезд-солнц. Конечно, мы можем утешать себя мечтою о дирижабле, несущемся со скоростью, близкой к скорости света; тогда человеческой жизни хватило бы для достижения соседних звезд[25]. Но если мы желаем оставаться на почве трезвых расчетов, нам придется ограничить поле своих небесных странствований пределами солнечной системы. Не будем скрывать от себя той безотрадной истины, что мы в праве говорить лишь о межпланетных, но никак не о межзвездных путешествиях...
Скорость света есть самая большая скорость, какая возможна в природе. Поэтому — если только не найдено будет средства продлить человеческую жизнь — земные люди никогда, ни при каких успехах техники, не достигнут звезд, удаленных от Земли дальше, чем на 50-60 „световых лет". Более далеких звезд смогут достичь лишь люди, родившиеся в пути, во время межзвездного странствования, и никогда не видевшие Земли. А ведь за этим недостижимым для смертного рубежом простирается еще целая вселенная!
X.
Жизнь на корабле вселенной.
С завистью думает современный астроном о тайнах мироздания, которые увидит из стеклянных окон своего межпланетного корабля будущий моряк вселенной. То, что смутно рисует нам слабый луч света, едва улавливаемый телескопом, во всем величии предстанет изумленному взору космического путешественника. И кто предскажет, кто предугадает, как чудесно расширятся тогда наши знания о мире миров, какие новые тайны исторгнет человеческий разум из глубин вселенной!
Но необычайное и новое ожидает будущего небесного странника не только за стенами его корабля. Внутри межпланетного дирижабля он сможет наблюдать целый ряд необыкновенных явлений, которые в первые дни путешествия будут, пожалуй, привлекать его внимание и поражать ум не менее, чем величественная панорама, расстилающаяся за окнами каюты.
Едва ли кто-нибудь даже во сне переживал ощущения, подобные тем, какие предстоит испытать будущему космическому страннику внутри его межпланетного корабля. Ощущения эти будут поистине фееричны. В коротких словах, речь идет о том, что внутри межпланетного снаряда нет тяжести: все предметы полностью утрачивают в нем свой вес! Закон тяготения словно отменяется в этом маленьком мире. Достаточно лишь немного подумать, чтобы убедиться в бесспорности этого вывода. Но трудно привыкнуть к мысли, что внутри небесного корабля не обнаруживается ни одно из тех проявлений силы тяжести, к которым мы так привыкли на Земле.
Допустим сначала, ради простоты, что „Ракета" Циолковского (или пушечное ядро Жюля Верна) свободно падает в мировом пространстве. Сила внешнего тяготения должна действовать одинаково как на самый снаряд, так и на предметы внутри него: поэтому она должна сообщать им равные перемещения (ведь тяжелые и легкие тела падают с одинаковою скоростью). Следовательно, все предметы внутри будут оставаться по отношению к его стенкам в покое. Разве может тело „упасть" на пол каюты, если пол этот сам „падает" с точно такою же скоростью?
Вообще, всякое падающее тело ничего не весит! Еще Галилей в своем бессмертном „Собеседовании и математических доказательствах относительно двух новых наук" писал об этом в следующих картинных выражениях:
„Мы ощущаем груз на наших плечах, когда стараемся мешать его падению. Но если станем двигаться вниз с такою же скоростью, как и груз, лежащий на нашей спине, то как же может он давить и обременять нас? Это подобно тому, как если бы мы захотели поразить копьем кого-либо, кто бежит впереди нас с такою же скоростью, с какою движемся и мы".
Полная невесомость
При всей своей простоте, мысль эта настолько непривычна, настолько неожиданна, что, даже будучи понята, неохотно принимается сознанием. Остановимся же на ней немного дольше. Перенесемся мысленно, например, внутрь Жюль-Вернового ядра, свободно падающего в мировом пространстве. Вы стоите на полу каюты и выпускаете из рук карандаш. Естественно, вы ожидаете, что он упадет на пол. Так полагал и Жюль Верн, не продумавший до конца своей собственной идеи. Но не то случится в действительности: карандаш повиснет в воздухе, ни на йоту не приближаясь к полу! В мировом пространстве, по отношению к Земле, он, конечно, будет перемещаться под действием земного притяжения — но не забывайте, что точно такое же перемещение под действием тяжести получит и само ядро. Если, например, земное притяжение в течение секунды приблизит карандаш к Земле на одну сажень, то и все ядро приблизится на одну сажень: расстояние между карандашом и полом каюты не изменится, а, следовательно, падение предметов внутри каюты не обнаружится.
Так будет не только при падении небесного снаряда на Землю, но и при полете его вверх и вообще при всяком свободном движении его по инерции в любом направлении в „поле тяготения". Ядро, летящее вверх, в сущности, тоже падает: скорость его взлета все время уменьшается под действием земного притяжения на определенную величину, — на ту именно, на которую ядро опустилось бы за тот же промежуток времени, если бы ему не сообщено было движения вверх. То же самое должно происходить, конечно, и со всеми предметами внутри снаряда. Вы помните, как в романе „Вокруг Луны" труп собаки, выброшенный пассажирами из окна, продолжал в мировом пространстве следовать за ядром, а вовсе не упал на Землю? „Этот предмет, — замечает романист, — казался неподвижным, как и ядро, и, следовательно, сам летел вверх с такою же скоростью". Но если предмет казался неподвижен вне ядра, то почему должен он перестать казаться таким внутри ядра? Удивительно, как часто люди подходят близко к истине и, не заметив ее, проходят мимо...
Теперь, думается, читатель достаточно убедился уже, что внутри межпланетного снаряда не может наблюдаться падения тел. Но если предметы в каюте небесного корабля не могут падать, то не могут они и оказывать давления на свои опоры. Короче говоря, в межпланетном снаряде все предметы становятся абсолютно невесомы[26].
Снаряд – планета
Строго говоря, в этом любопытном факте не должно бы быть для нас ничего неожиданного или нового. Мы, ведь, нисколько не изумляемся, например, тому, что на Луне все тела тяготеют не к Земле, а к центру Луны. С какой же стати предметы внутри небесного корабля должны падать к Земле? Ведь мы знаем, что с того момента, как „Ракета", прекратив работу двигателя, изменяет свой путь единственно лишь под действием притяжения Земли или иных мировых тел, — она превращается уже в миниатюрную планету, в самостоятельный мир, имеющий свое собственное, хотя и ничтожное, напряжение тяжести. Внутри снаряда могло бы проявляться разве лишь взаимное притяжение предметов и притягательное действие стенок снаряда. Но нам известно уже, как ничтожно взаимное притяжение мелких тел и какие медленные, незаметные движения оно способно вызвать. А влияние притяжения стенок снаряда должно быть еще незаметнее: в небесной механике доказывается, что если бы снаряд был строго шарообразный, то притягательное действие такой оболочки равнялось бы нулю, так как притяжение любого ее участка уравновешивалось бы обратным действием диаметрально противоположного участка.
По этому признаку — полному отсутствию тяжести — будущие пассажиры межпланетного корабля безошибочно смогут определить, не глядя в окно, движутся ли они вне Земли или нет. Для них совершенно немыслимы сомнения в роде тех, которые, по описанию Жюля Верна, будто бы смущали пассажиров в первые минуты межпланетного полета: — „Николь, движемся ли мы?
„Николь и Ардан переглянулись: они не чувствовали движения ядра.
— „Действительно: движемся ли мы? — повторил Ардан.
— „Или спокойно лежим на почве Флориды? — спросил Николь.
— „Или на дне Мексиканского залива!.. — прибавил Мишель".
Подобные сомнения совершенно невозможны для пассажиров свободно брошенного межпланетного корабля. Им не придется заглядывать в стеклянные окна своей каюты, чтобы решить, движутся ли они: непосредственное ощущение невесомости сразу укажет им, что они уже перестали быть пленниками Земли и превратились в обитателей новой миниатюрной планетки, лишенной тяжести.
Мы так привыкли к силе тяжести, не покидающей нас ни в железнодорожном вагоне, ни на палубе парохода, ни даже в корзине аэростата или в сидении аэроплана — мы так сжились с этой неустранимой силой, что нам крайне трудно представить себе ее отсутствие. Чтобы помочь читателю вообразить себе, при каких необычайных, почти сказочных условиях будет протекать „невесомая" жизнь пассажиров в каюте межпланетного корабля, попытаемся набросать здесь в главнейших чертах своеобразную картину этой жизни.
Сказочные условия жизни
Вы пробуете сделать шаг в каюте небесного корабля — и плавно, как пушинка, парите к потолку: легкое усилие мускулов ваших ног вполне достаточно, чтобы сообщить вашему невесомому телу заметную поступательную скорость. Вы летите к потолку (нельзя сказать „вверх": ведь в мире без тяжести нет ни верха, ни низа), ударяетесь о него — и обратный толчок относит ваше невесомое тело снова к полу. Это падение не будет грузным; вы почувствуете довольно легкий удар, но его достаточно, чтобы опять оттолкнуть вас к потолку, и т. д. Если, желая как-нибудь прекратить невольные и бесконечные колебания, вы ухватитесь за стол, то нисколько не пособите делу: стол, ничего не весящий, легко полетит вместе с вами, и будет качаться туда и назад, попеременно отталкиваясь от потолка и пола. К чему бы вы ни прикоснулись — все немедленно же приходит в движение, медленное, но зато нескончаемое. Полка с книгами поплывет в воздухе, не растеривая своих книг; ящик с провизией и посудой будет лететь „вверх дном", не роняя своего содержимого. Словом, в каюте небесного корабля будет царить полный хаос, исключающий всякую возможность покойной жизни, если мы заранее не позаботимся привязать и привинтить все вещи к полу, к стенам, к потолку.
Впрочем, многие предметы обстановки будут совершенно излишни в этом мире без тяжести. К чему вам стулья, если вы можете висеть в воздухе в любом положении, не утомляя ни единого мускула? Стол тоже довольно бесполезен: все поставленное на него унесется, как пух, при малейшем толчке или дуновении. Лучше заменить стол особым станком с зажимами. Не нужна вам и кровать: ведь вы не удержитесь на ней ни одной минуты — при малейшем движении улетите прочь; пружинный матрац будет бросать ваше тело к потолку, как мяч. Чтобы спать покойно, без невольных странствований по всем углам каюты, вам необходимо будет пристегнуть себя ремнями к своему ложу. Перина — совершенно излишний предмет там, где нет тяжести: вам будет очень мягко и на жестком полу: ведь ваше тело ничего не весит, оно не давит на пол, а, следовательно, вы не будете испытывать ощущения жесткости. Как сказочный Левиафан, который –
На острых камнях возлегает
И твердость оных презирает.
Для крепости великих сил
Считает их за мягкий ил,
вы, как на мягком иле, сможете нежиться на жестком ложе, „презирая" его твердость.
Жидкости в невесомой среде
Буквально на каждом шагу будет подстерегать вас неожиданное и необычайное! Вы хотите налить воды для питья: опрокидываете графин над стаканом, но — вода не льется... Нет тяжести, следовательно, нет и причины, побуждающей жидкость выливаться из опрокинутого сосуда. Вы ударяете рукой по дну графина, чтобы вытряхнуть из него воду, и — новая неожиданность: из графина вылетает большой колеблющийся водяной шар, плавно движущийся в воздухе. Это не что иное, как огромная водяная капля: в мире без тяжести жидкости принимают сферическую форму, как масло в знаменитом опыте Плато. Если эта гигантская водяная капля ударится о пол или стенку каюты, она растечется по ним тончайшим слоем и расползется во все стороны. Пить в межпланетном дирижабле нельзя будет так, как мы привыкли. Зачерпнуть жидкость мудрено: она соберется в шар, если она не смачивает стенок сосуда; и тогда вы не донесете до рта этой водяной пилюли, — при малейшем толчке она умчится прочь. Если же жидкость смачивает стенки посуды, то облечет ее ровным жидким слоем со всех сторон, — и вам придется подолгу облизывать сосуд, испытывая муки Тантала.
Тепловые явления
Приготовление обеда из невесомых продуктов тоже будет сопряжено с немалыми и довольно неожиданными затруднениями. Чтобы довести воду до кипения, придется повозиться чуть не целые сутки. В самом деле: при обычных условиях вода в кастрюле нагревается сравнительно быстро только потому, что нижние, нагретые слои воды, как более легкие, поднимаются вверх, вытесняясь холодными, выше лежащими; перемешивание это происходит само собой, пока все слои воды не нагреются до кипения. Но пробовали ли вы нагревать воду сверху? Попробуйте — вы убедитесь, что это бесконечная история: нагретый слой останется наверху, теплота будет передаваться нижележащим слоям только через воду же, — а теплопроводность воды, как известно, ничтожна; можно довести воду вверху сосуда до кипения и в то же время удерживать на его дне нерастаявшие куски льда. В невесомом мире небесного корабля также не будет этого благодетельного перемешивания слоев при нагревании жидкости, — так как нагретые и ненагретые слои одинаково невесомы — а следовательно, вскипятить всю воду в кастрюле обычным путем будет довольно трудно. В невесомой кухне невозможно и жарить на открытой сковородке: упругие пары масла тотчас же отбросят жаркое к потолку. По той же причине — отсутствию перемещения нагретых частей, — весьма трудно будет отопить каюту каким-либо нагревательным прибором.
Невесомое пламя
Даже обыкновенное пламя не будет гореть в каюте небесного корабля. Образующиеся при горении пламени негорючие газы — углекислота, водяной пар и др. — не могут здесь удаляться сами собой, как на Земле, вследствие своей высокой температуры и легкости. Они будут оставаться тут же, окружая огонь и прекращая к нему доступ воздуха. Пламя задохнется в продуктах собственного горения. Ведь тушение пожаров на том и основано, что, заливая пламя водой, мы облекаем его негорючими водяными парами и тем прекращаем доступ к нему воздуха. В каюте космического корабля это тушение будет происходить само собою. Устроив в фантастическом, вагоне-ядре газовое освещение, Жюль Верн в сущности обрек своих героев на пребывание в темноте. В будущем межпланетном снаряде освещение необходимо устроить электрическое, и даже для кухни придется пользоваться исключительно электрическими беспламенными нагревателями.
Безвредность отсутствия веса
А не отразится ли полное отсутствие тяжести на отправлениях человеческого организма? К счастью, можно думать, что нет. Дыхание, кровообращение и все другие функции почти совершенно не зависят от тяжести; это видно хотя бы уже по той легкости, с какой мы обычно меняем вертикальное положение своего тела на горизонтальное. Если бы отсутствие веса было смертельно, мы умирали бы при каждом прыжке, так как, падая, мы на мгновение лишаемся веса и уподобляемся пассажирам небесного корабля: вес есть давление на опору, а при свободном падении тело не имеет опоры — поэтому оно не имеет и веса[27]. Путешествие по океану вселенной, если только оно благополучно началось, будет, во всяком случае, менее опасно для здоровья пассажиров, чем плавание по водяному океану, сопряженное с морской болезнью.
Все эти житейские неудобства — курьезные, необычайные, неожиданные, но по существу безвредные и невинные,— заставят будущих моряков вселенной отрешиться от многих глубоко укоренившихся привычек. Едва ли, однако, кто-нибудь откажется из-за этого совершить путешествие в таинственные глубины мироздания. Люди терпели более серьезные лишения, чтобы изучить нашу маленькую Землю, и, конечно, не остановятся перед ними, когда дело будет идти об исследовании вселенной.
XI.
Заключение.
Никогда не говори „никогда".
Итак, если суждено человечеству когда-нибудь вступить в прямое сообщение с другими планетами, включить их в круг своего непосредственного изучения, быть-может, даже колонизовать их или приобщить к сфере добывающей промышленности, — словом, если земному человечеству предстоит вступить в новый „вселенский" период своей истории — то осуществится это, всего вероятнее, при помощи исполинских ракет и вообще реактивных приборов. Это единственный намечающийся в настоящее время путь к практическому разрешению проблемы межпланетных путешествий.
Гений Ньютона открыл человечеству нерушимый закон действия могучей силы, которая извечно приковывает нас к Земле. Но тот же гений провозгласил и другой закон "природы, опираясь на который потомки наши когда-нибудь свергнут иго тяжести и вырвутся из земного плена на простор вселенной, в необъятный мир миров.

ПРИБАВЛЕНИЯ
К главе II
1. Силы тяготения
Приведенные в начале главы II примеры действия силы тяготения могут быть проверены несложными расчетами, основанными, на законе Ньютона и элементах механики. Напомним сначала, что в механике за единицу измерения силы принята сила, которая, будучи приложена к свободному телу в 1 грамм, ежесекундно увеличивает его скорость на 1 сантиметр. Эта сила называется диной. Так как сила земного притяжения ежесекундно увеличивает скорость свободно падающего грамма почти на 1.000 сантиметров (10 метров), то сила, с какой притягивается к Земле 1 грамм, больше „дины" в 1.000 раз, т. е. равна (почти) 1.000 динам. Другими словами: вес гирьки в 1 грамм (сила ее притяжения к Земле) равен 1.000 динам. Это дает нам представление о величине дины в едицицах веса: дина почти равна 1.000-й доле грамма.
Далее: точными измерениями установлено, что два шарика, по 1 грамму каждый, расстояние между центрами которых равно 1 сантиметру, притягиваются между собою с силою в одну 15-миллионную долю дины,. Эту величину часто называют „постоянной тяготения".
Зная это, уже не трудно, пользуясь законом Ньютона, вычислить силу взаимного притяжения двух человеческих тел, разделенных промежутком в 1 сажень (2 метра, или 200 сант.). Принимая вес человеческого тела в 4 пуда, или 65 килограммов (65.000 граммов), и имея в виду, что взаимное притяжение прямо пропорционально произведению масс и обратно пропорционально квадрату расстояния (закон Ньютона), — имеем для силы взаимного притяжения

Итак, два человеческих тела притягиваются взаимно с силою 0,007 дины (это менее 100-й доли дины, т. е. менее 100-й доли миллиграмма).
Чтобы вычислить, какой путь пройдут оба тела в течение часа под влиянием этой силы, мы воспользуемся формулой:

где t — число секунд, и а — ускорение, т. е. сила (0,007 дины), деленная на массу (65000 гр.). Следовательно, каждое тело пройдет в 3.600 секунд:

А оба тела сблизятся на 0,7 сант. + 0,7 сант.= 1,4 сант.[28].
Таким же образом может быть вычислена сила взаимного притяжения и двух дредноутов, разделенных расстоянием в 1 километр. Масса каждого корабля — 25.000 тонн = 25.000.000 килогр. = 25.000.000.000 граммов; расстояние 1 килом. =100.000 сант. Поэтому взаимное притяжение равно

Так как 1.000 дин = 1 грамму, а грамм — около ¼ золотника, то 4.100 дин почти равно 1 золотнику.
Величина сближения кораблей под действием этой силы в течение первого часа равна

Сложнее вычислить время обращения тяготеющих тел одного вокруг другого (точнее — вокруг их общего центра тяжести), но и этот расчет может быть выполнен элементарным приемом. Вернемся к примеру двух человеческих тел и допустим, что эти тела представляют собою систему обращающихся тел. Массы их равны между собою, а потому оба тела должны обращаться вокруг точки, расположенной в середине между ними, т. е., принимая орбиту за круг, имеем, что радиус ее = 100 сант. Величина центростремительной силы кругового движения равна, как известно из механики  , где m — масса, v — скорость, R — радиус круга. Скорость v можно выразить через длину орбиты 2πR, деленную на продолжительность оборота t, т.-е. через
, где m — масса, v — скорость, R — радиус круга. Скорость v можно выразить через длину орбиты 2πR, деленную на продолжительность оборота t, т.-е. через  . Следовательно,
. Следовательно,

С другой стороны, центростремительная сила должна быть равна силе взаимного притяжения обращающихся тел — иначе кругового движения не могло бы быть. Эта сила выражается формулой

где k — „постоянная тяготения", т-е.  дины.
дины.
Приравнивая оба выражения:

определяем из этого равенства величину t, т.-е. продолжительность обращения:

откуда

Подставляя для нашего случая вместо R-100 см., m — 65.000 и зная, что π = 3,14,

имеем:

Следовательно, время обращения двух человеческих тел, кружащихся под действием силы взаимного тяготения по круговой орбите с диаметром 2 метра, равно 190.284 сек., или 53,6 часа (около двух суток)[29].
Как вычислить время взаимного падения тяготеющих друг к другу тел, — показано далее, в статье „Падение в мировом пространстве".
В заключение приводим интересный отрывок, характеризующий силу тяготения и заимствуемый у известного английского физика О. Лоджа[30]:
„Силы тяготения между небольшими телами незначительны и далеко превосходятся магнитными. Действительно, притяжение между телами определенной малости может быть более чем уравновешено даже давлением, возникающим вследствие их взаимного излучения, несмотря на то, что это давление почти бесконечно мало. Отсюда следует, что достаточно малые тела любой температуры отталкивают друг друга (если только они не заключены в оболочку постоянной температуры, где лучистое давление на них со всех сторон одинаково).
Размеры, при которых лучистое отталкивание перевешивает тяготение, в случае двух равных шаров, зависят от температуры шаров и от их плотности; по данным проф. Пойтинга, при обыкновенной, привычной для нас температуре— скажем, при 16° Ц. — равенство этих двух сил для двух деревянных шаров, расположенных в пространстве, достигается тогда, когда каждый шар имеет диаметр приблизительно в один фут. Для тел меньших размеров или более горячих лучистое отталкивание пересиливает взаимное тяготение; отталкивание это возрастает пропорционально четвертой степени абсолютной температуры тел.
Притягательная сила тяготения между молекулами чрезвычайно мала; между двумя атомами или двумя электронами она настолько мала, что ею можно пренебречь, хотя бы расстояние между ними и не выходило из пределов размера молекулы.
А между тем, от совокупного притяжения мириад таких тел происходит результирующая сила тяготения, заметная на расстояниях в миллионы миль. Сила эта не только заметна, но величину ее нужно признать прямо-таки ужасающей.
Когда дело идет о телах астрономических размеров, сила тяготения перевешивает все другие силы; и все электрические и магнитные притяжения в сравнении с нею падают до полного ничтожества".
К главе IV
2. Теории тяготения
„Все сделанные попытки объяснить силу тяжести, как результат движения в среде, находящейся между телами, наталкиваются на то затруднение, что тяжесть беспрепятственно проходит сквозь тела, как бы велики и плотны они ни были, — пишет Аррениус[31]. — Так, например, притяжение Солнца действует на частицу, лежащую в центре Земли, сквозь все промежуточные слои. А так как действие силы должно состоять в каком-нибудь изменении движения тела, подвергающегося ее влиянию, то необходимо принять, что частица, лежащая позади другой, подверженной той же силе, по крайней мере отчасти закрыта от этого влияния. Поэтому на соединительной линии между частицею в центре Земли и любою частицею на Солнце не должна была бы лежать ни одна из бесконечно большого числа тяжелых частиц верхних слоев Земли. Значит, необходимо предположить, что частицы, на которые действует сила тяжести, имеют бесконечно малое протяжение и должны считаться математическими точками. Физически этот взгляд немыслим. Точно также невозможно представить себе, чтобы математические точки могли возмущать движение. Удивительно, что та самая сила природы, которую мы точнее всего можем проследить посредством вычисления, в физическом отношении представляет величайшую загадку".
Совершенно особым образом подходит к вопросу новейшая (1915 г.) теория тяготения, разработанная А. Эйнштейном, которая вовсе не рассматривает тяготение как некоторую „силу". Исходным пунктом теории тяготения Эйнштейна являются следующие соображения[32]:
„Вообразим себе систему в виде большого ящика или комнаты и положим сперва, что она находится в гравитационном поле, т. е. в такой части пространства, в которой действуют силы тяготения, и что она в этом пространстве неподвижна. В виде примера представим себе, что она находится на земной поверхности, где гравитация, т. е. сила тяжести, действует вертикально вниз от потолка к полу комнаты. Наблюдатели, находящиеся в этой системе, заключают следующее. Тела, спокойно лежащие на полу, на столе и т. д., производят давление на тела, находящиеся под ними. Если взять в руку какое-либо тело, напр., свинцовый шарик, и отпустить его, то он начинает падать вертикально вниз с ускорением, которое мы обозначим буквой g, и которое оказывается независящим от рода тела, если исключить сопротивление воздуха. Если шарик бросить в горизонтальном направлении, то он начнет двигаться по кривой линии (по параболе) вниз, и на некотором расстоянии от наблюдателя достигнет пола. В обоих случаях мы имеем дело с весомой массой взятого тела.
„Теперь рассмотрим другой случай. Та же система находится в пространстве, в которого нет никакого гравитационного поля, но сама система движется с ускорением g по направлению, обратному тому направлению, в котором раньше действовала гравитация, т. е. [движется] по направлению от пола к потолку. Наблюдатель, находящийся внутри системы, замечает следующее. Все тела, спокойно лежащие на неподвижных предметах (пол, стол, рука), производят давление на свои опоры; такое же давление производит и сам наблюдатель хотя бы на пол ящика. Если наблюдатель выпустит из рук какой-нибудь предмет, напр., свинцовый шарик, то он увидит, что шарик движется по направлению к полу с ускорением g, между тем как наблюдателю, находящемуся вне ящика, тот же шарик представится неподвижным. Если наблюдатель бросит шарик по направлению, параллельному полу, то заметит, что шарик движется по кривой линии и на некотором расстоянии ударяется об пол. Наблюдателю, находящемуся вне ящика, представится, что шарик движется прямолинейно и равномерно по направлению, параллельному полу. Ясно, что для этого наблюдателя движение происходит по инерции и зависит от инертной массы шарика.
„Сравнивая явления, наблюдаемые в указанных двух случаях внутри системы, мы видим, что они вполне тождественны, хотя в первом случае они зависят от весомой массы тел, а во втором случае — от массы инертной. Наблюдатель, находящийся внутри ящика, не имеет возможности отличить эти два случая друг от друга, и он, например, во втором случае может предположить, что внутри ящика действует гравитационное поле. Все изложенное приводит нас к результату огромной важности. Наблюдатель, находящийся внутри системы, не имеет возможности отличить друг от друга прямолинейного равномерно-ускоренного движения системы от наличности внутри системы гравитационного поля. Все явления происходят внутри системы совершенно одинаково в обоих случаях. Мы можем сказать, что гравитационное поле и равноускоренное прямолинейное движение системы друг другу эквивалентны[33]. Для Эйнштейна эквивалентность настолько полна, что он вообще всякое ускорение системы отождествляет с возникновением гравитационного поля".
Исходя из этого, Эйнштейн развивает стройную теорию тяготения, принципиально отличную от всех прежде предлагавшихся и уже получившую частичное подтверждение согласием ее неожиданных следствий с наблюдениями.
К сожалению, эта теория не может быть общепонятно изложена.
К главе IV
3. Поглощение тяготения
Вопрос о существовании такого вещества, которое было бы вполне или отчасти непроницаемо для тяготения (т. е. обладало бы свойствами фантастического „кеворита", упоминаемого в романе Уэльса), служил неоднократно предметом научного рассмотрения. До самого последнего времени опыты, производившиеся с целью обнаружить хотя бы следы подробного поглощения тяготения, не давали положительных результатов. Лишь в 1920 г. удалось[34], повидимому, получить результат, который указывает на некоторое ослабление силы тяготения, при действии ее через тела большой плотности (ртуть, свинец). При этих опытах свинцовый шар, весом около 1300 килогр., окружался 100 килогр. ртути так, чтобы она не касалась шара: при этом наблюдалось уменьшение веса свинцового шара на 2 миллионные доли грамма.
В другой серии опытов того же ученого тяготение действовало через толстый слой свинца (именно, через призму весом 600 пудов, при этом вес шара уменьшался на 2 миллионных грамма).
Однако, интересные данные этих опытов далеко нельзя считать решающими; они нуждаются в тщательной проверке новыми опытами, с целью установить, действительно ли уменьшение веса в данном случае обусловлено поглощением тяготения, а не вызывается какими-либо другими причинами.
К главе VII
4. Падение в мировом пространстве
Полет пушечного ядра Жюля Верна на Луну можно рассматривать как случай падения тела в мировом пространстве под влиянием силы тяготения. Поэтому, прежде чем рассматривать условия его полета, полезно рассмотреть такую, например, задачу из области небесной механики:
Во сколько времени упал бы на Солнце земной шар, если бы по какой-либо причине прекратилось его движение по орбите?
Задачи подобного рода легко разрешаются на основании третьего закона Кеплера: квадраты времен обращения (планет и комет) относятся как кубы их средних расстояний от Солнца. В нашем случае мы можем земной шар, летящий прямо к Солнцу, уподобить воображаемой комете, движущейся по сильно вытянутому и сжатому эллипсу, крайние точки которого расположены: одна — близ земной орбиты, другая — в центре Солнца. Среднее расстояние такой кометы от Солнца, очевидно, вдвое меньше среднего расстояния Земли. Вычислим, каков должен был бы быть период обращения этой воображаемой кометы. Составим на основании третьего закона Кеплера, пропорцию:

Период обращения Земли равен 365 сутк.; среднее расстояние ее от Солнца примем за единицу, и тогда ср. расст. кометы выразится ½. Пропорция принимает вид:

откуда

или:

Но нас интересует не полный период обращения этой воображаемой кометы, а половина периода, т.-е. продолжительность полета в один конец — от земной орбиты до Солнца: это и будет искомое время падения Земли на Солнце. Оно равно

Итак, чтобы узнать, во сколько времени Земля упала бы на Солнце, нужно продолжительность года разделить на √32, т.-е. на 5,6.
Легко видеть, что полученная простая формула применима не к одной только Земле, но и ко всякой другой планете и даже ко всякому спутнику. Иначе говоря: чтобы узнать, во сколько времени планета или спутник упадут на свое центральное светило, нужно период их обращения разделить, на √32, т.-е. на 5,6. Меркурий, обращающийся в 88 дней, упал бы на Солнце в 15½ дней; Нептун, период обращения которого равняется 30 нашим годам, — падал бы на Солнце в течение 5½ лет. А Луна упала бы на Землю в 27,3:5,6, т.-е.. почти ровно в 5 дней. И не только Луна, но и всякое вообще тело, находящееся от нас на расстоянии Луны, падало бы на Землю в течение 5 дней (если только ему не сообщена начальная скорость, а падает оно, подчиняясь лишь действию одного земного притяжения). Здесь мы вплотную подходим к задаче Жюля Верна. Легко понять, что столько же времени, 5 дней, должно лететь на Луну всякое тело, брошенное, наоборот, с Земли на Луну с такою скоростью, чтобы как-раз достичь расстояния Луны. Значит, алюминиевое ядро Жюля Верна должно было бы лететь 5 суток, если бы его хотели закинуть на расстояние Луны.
Однако, члены Пушечного Клуба рассчитывали закинуть ядро не прямо до Луны, а только до той точки между Землей и Луной, где сила притяжения обоих светил уравновешивается: отсюда ядро под действием своей тяжести само уже упало бы на Луну, притягиваемое ею. Это „нейтральная" точка находится на 0,9 расстояния от Земли.
Вычисление, следовательно, несколько усложняется. Во-первых, нужно вычислить, во сколько времени ядро долетело бы до 0,9 расстояния между Землей и Луной, или, — что то же самое, — во сколько времени тело с этого расстояния упало бы на Землю; во-вторых, надо определить продолжительность падения тела от этой нейтральной точки до Луны.
Для решения первой задачи представим себе, что на 0,9 расстояния от Земли до Луны обращается вокруг нашей планеты небесное тело, и вычислим период обращения этого воображаемого спутника Земли. Обозначив неизвестный период обращения через х, составляем, на основании третьего Кеплерова закона, пропорцию:

отсюда искомый период обращения = 27,3√0,93= 23,3. Разделив этот период на √32, т.-е. на 5,6, мы, согласно выведенной ранее формуле, получим время перелета ядра от Земли до нейтральной точки: 23,3:5,6 = 4,1 суток.
Вторую задачу решаем сходным образом. Чтобы вычислить, во сколько времени ядро упало бы с расстояния нейтральной точки до Луны, нужно сначала определить, во сколько времени ядро, находясь на том же расстоянии от Луны, совершило бы вокруг нее полный оборот. Радиус орбиты этого воображаемого спутника Луны равен 0,1 радиуса лунной орбиты, а масса центрального светила (в данном случае Луны) — в 81 раз меньше массы Земли. Если бы масса Луны равнялась земной, то спутник, обращаясь на среднем расстоянии вдесятеро меньшем, чем лунное, совершал бы полный оборот в период y, легко вычисляемый по закону Кеплера:

Но так как масса, а следовательно и притягательное действие центрального светила в данном случае в 81 раз меньше, чем в системе Земли, то время обращения ядра-спутника будет дольше. Во сколько раз? Из механики мы знаем, что центростремительное ускорение пропорционально квадрату скорости. Здесь это ускорение (производимое притяжением Луны) меньше в 81 раз, — следовательно, скорость движения ядра по орбите должна быть меньше в √81, т.-е. в 9 раз. Другими словами, ядро в роли лунного спутника должно обегать кругом Луны в 9 раз медленнее, чем оно обходило бы, на таком же расстоянии, вокруг Земли. Значит, искомое время обращения равняется: 0,273√10 × 9 = 7,77 суток.
Чтобы получить продолжительность падения ядра от нейтральной точки до Луны, нужно, как мы уже знаем, найденный сейчас период его обращения (7,77) разделить на √32, т.-е. на 5,6; получим 1,4 суток[35].
Итак, весь перелет пушечного снаряда от Земли до Луны должен был бы длиться 4,1+1,4 сут. = 5,5 сут.
Это, конечно, не вполне точный результат: здесь не принято во внимание то обстоятельство, что и при полете от Земли до нейтральной точки ядро подвергается притягательному действию Луны, ускоряющему его движение; с другой стороны, при падении от этой точки на Луну оно испытывает на себе замедляющее действие земного притяжения. Последнее действие должно быть особенно заметно и, как показывает более точное вычисление, почти вдвое увеличило бы продолжительность падения ядра от нейтральной точки до Луны. Благодаря этим поправкам, общая продолжительность перелета снаряда от Земли до Луны с 5½ суток возрастает до 6½ суток.
В романе продолжительность перелета определена „астрономами Кембриджской обсерватории" в 97 час. 13 мин. 20 сек., т.-е. в 4 с небольшим суток, вместо 5½ и даже 6½ суток. Жюль Верн ошибся на двое суток. По-видимому, французский романист, или лицо, производившее для него расчеты, преуменьшили время падения ядра от нейтральной точки до Луны: в романе оно определено всего в 13 час. 53 мин., между тем как, вследствие слабости лунного притяжения, это падение должно было совершаться гораздо медленнее и занять около 60 часов.
В заключение, рассмотрим случай взаимного падения друг на друга тел равной массы. Строго говоря, мы имеем взаимное падение во всех случаях: когда ядро падает на Луну, или камень на Землю, то и Луна одновременно падает на ядро, а Земля на камень. Но скорости перемещения огромных масс Луны и Земли в этих случаях так ничтожны, что ими пренебрегают: они меньше скорости падения ядра или камня во столько же раз, во сколько масса Луны или Земли больше массы или камня. Иное дело, когда массы тяготеющих друг к другу тел равны (или близки по величине): тогда скорости падающих друг на друга тел равны (или близки к равенству), и рассматривать процесс падения тел как процесс односторонний уже нельзя.
Итак, остановимся на примере взаимного падения двух звезд двойной звезды в случае равенства их масс. Установим зависимость между продолжительностью такого падения и периодом обращения звезд по их круговой орбите. Вообразим, что обе звезды, вместо того, чтобы обращаться по кругу радиуса В, движутся по весьма вытянутому эллипсу, „большая ось" которого совпадает с одним из диаметров круга. Среднее расстояние звезды, при таком движении, от общего центра тяжести системы (вокруг которого фактически совершается обращение) равно

Применяя к обеим парам третий закон Кеплера, имеем

Обозначив период кругового движения через t, имеем

или:

Но легко сообразить, что искомое время падения звезды от точки круговой орбиты до центра составляет ⅓ периода полного обращения по крайне вытянутому эллиптическому пути, — т.-е. искомое время падения =

Выше, на стр. 96-й, мы вычислили, что два человеческих тела должны были бы, обращаясь вокруг общего центра тяжести по круговой орбите диаметром 2 метра, совершать полный оборот в 53,6 часа. Разделив этот период на 11,28, получим продолжительность взаимного падения
53,6 час.: 11,28 = 4,75, т.-е. около 5 часов.
(Предоставляем читателю сделать подобный же расчет для случая двух дредноутов, рассмотренного в прибавлении 1).
К главе VII
5. Успехи современной артиллерии
Дальность полета ядер, извергаемых новейшими пушками (1922 г.), превзошла даже и те невероятные расстояния, которые преодолевались к концу мировой войны германской артиллерией (т.-е. 80—100 верст). Это стало возможным, главным образом,, благодаря тому, что ядра с большою начальною скоростью закидываются на высоту, где сопротивление воздуха, вследствие его разреженности, весьма незначительно. Снаряд весом 100 килогр. (6 пудов), извергнутый с начальной скоростью 1400 метров (1⅓ версты), быстро проносится через низшие, сравнительно плотные, слои атмосферы и уже на высоте 30 километров попадает в область, где воздух раз в 80 реже, чем близ земной поверхности[36]. Здесь сопротивление среды настолько незначительно, что ядро может пролететь большое расстояние без заметного уменьшения своей скорости.
По газетным сведениям, в Соединенных Штатах Америки уже сооружаются орудия с дальностью полета ядер 200 — 300 верст!
Надо упомянуть еще, что кроме взрывчатых веществ, существует и другое средство сообщить метаемому снаряду большую начальную скорость: выталкивание электромагнитными силами. Теоретически и лабораторно электромагнитные пушки вполне разработаны и оправдывают уже и в настоящее время возлагаемые на них надежды. Теоретики воздухоплавания не отрицают даже возможности полетов людей на таких аппаратах — т.-е. реального осуществления Жюль-Вернова ядра.. „Электрические методы сообщения снаряду начальной скорости, достаточной не только для короткого полета, но даже для прохода весьма значительной дистанции, уже составляют столь крупный шаг вперед в технике аппаратов, основанных на принципе поддержания при помощи начальной скорости, что возможность осуществления полетов на таких аппаратах не может быть вполне отрицаема: необходимо разработать метод безопасного спуска таких снарядов и ограничить развитие внутри его температуры [вследствие трения о воздух] в допустимых для „человека пределах (А. Вегенер. „Самолет будущего", „Вестник Возд. Флота", 1922, № 13).
К главе VIII
6. Давление внутри пушечного ядра
Для читателей, которые пожелали бы проверить расчеты, упомянутые на стр. 65-й, приводим здесь эти несложные вычисления.
Для расчетов нам придется пользоваться лишь двумя формулами ускоренного движения, именно:
1) Скорость v в конце t-ой секунды равна at, где а — ускорение:
v = at.
2) Пространство S, пройденное в течение t секунд, определяется формулой:

По этим двум формулам легко определить (разумеется, только приблизительно) ускорение движения ядра, когда оно скользило в канале грандиозной Жюль-Верновой пушки.
Нам известна из романа длина пушки — 210 метров: это и есть пройденный телом путь S. Романист указывает и скорость ядра у выхода из орудия: 16.000 метров. Данные эти позволяют нам определить прежде всего величину t — продолжительность движения снаряда в канале орудия (рассматривая это движение, как равномерно-ускоренное). В самом деле:

Итак, оказывается, что ядро скользило внутри пушки всего 1/40 секунды.

Значит, ускорение ядра при движении в канале = 640.000 метров в секунду, т. е. в 64.000 раз больше ускорения силы земной тяжести!
Какой же длины должна быть пушка, чтобы это ускорение было всего в 20 раз больше ускорения тяжести (т.-е. равнялось. 200 метрам)?
Это задача, обратная той, которую мы только что решили. Данные: a = 200 метров; v= 11000 метров (при отсутствии сопротивления атмосферы такая скорость достаточна)..
Из формулы v = at имеем: 11000 = 200t, откуда t=55 секундам.
Из формулы

получаем, что длина пушки должна равняться

метров, т.-е. круглым. счетом около 300 верст.
К главе IX
7. Проект Кибальчича
„Когда я явился к Кибальчичу, — говорил судьям, его защитник, — меня прежде всего поразило, что он был занят совершенно иным делом, ничуть не касающимся настоящего процесса. Он был погружен в изыскание, которое он делал о каком-то воздухоплавательном снаряде; он жаждал, чтобы ему дали возможность написать свои математические изыскания об этом изобретении. Он их написал и представил по начальству".
Начальник жандармского управления, получив рукопись Кибальчича, передал ее в департамент полиции. Там решили, что „давать ее на рассмотрение ученых теперь едва ли своевременно и может вызвать только неуместные толки", — а потому проект был запечатан в конверт и подшит к делу. С 1882 г. по август 1917 г. пакет хранился нетронутым в секретных архивах департамента полиции. Вся история авиации — от первых попыток Райтов до мощных военных аэропланов — успела развиться, — а проект русского революционера, одна из самых смелых технических идей, какие когда-либо рождались в уме человека — лежал безвестно для мира в архивной пыли.
Ниже мы приводим извлечение из этой рукописи Кибальчича (помеченной 23 марта 1881 г.):
Проект воздухоплавательного прибора
бывшего студента института инженеров путей сообщения, Николая Ивановича Кибальчича, члена русской социально-революционной партии.
„Находясь в заключении, за несколько дней до своей смерти, я пишу этот проект. Я верю в осуществимость моей идеи, и эта вера поддерживает меня в моем ужасном положении.
„Если же моя идея, после тщательного обсуждения учеными специалистами, будет признана исполнимой, то я буду счастлив тем, что окажу громадную услугу родине и человечеству. Я спокойно тогда встречу смерть, зная, что моя идея не погибнет вместе со мной, а будет существовать среди человечества, для которого я готов был пожертвовать своею жизнью. Поэтому я умоляю тех ученых, которые будут рассматривать мой проект, отнестись к нему как можно серьезнее и добросовестнее и дать мне на него ответ как можно скорее.
„Прежде всего считаю нужным заметить, что, будучи на свободе, я не имел достаточно времени, чтобы разработать свой проект в подробностях и доказать его осуществимость математическими вычислениями. В настоящее же время, я, конечно, не имею возможности достать нужные для этого материалы. Следовательно, эта задача — подкрепление моего проекта математическими вычислениями — должна быть сделана теми экспертами, в руки которых попадет мой проект. Кроме того, я не знаком с той массой подобных же проектов, которая появилась за последнее время, т.-е., вернее сказать, мне известны приблизительно идеи этих проектов, но неизвестны те формы, в каких изобретатели думают осуществить свои идеи. Но, насколько мне известно, моя идея еще не была предложена никем.
„В своих мыслях о воздухоплавательной машине я прежде всего остановился на вопросе: какая сила должна быть употреблена, чтобы привести в движение такую машину"?
Отвергнув возможность применения к этой цели силы пара, электричества и мускульной силы человека, Кибальчич приходит к заключению, что источником применимой к воздухоплаванию силы могут быть лишь медленно горящие взрывчатые вещества.
„В самом деле, при горении взрывчатых веществ образуется более или менее быстро большое количество газов, обладающих, в момент образования, громадной энергией. Я не помню в точности, какую работу, если выразить ее в килограммометрах, производит воспламенение 1 фунта пороха, но, если не ошибаюсь, 1 фунт пороху, будучи взорван в земле, может выбросить земляную глыбу, весящую 40 пудов. Словом, никакие другие вещества в природе не обладают способностью развивать в короткий промежуток времени столько энергии, как взрывчатые.
„Но каким образом можно применить энергию газов, образующихся при воспламенении взрывчатых веществ, к какой-либо продолжительной работе? Это возможно только под тем условием, если та громадная энергия, которая образуется при горении взрывчатых веществ, будет образовываться не сразу, а в течение более или менее продолжительного промежутка времени.
„Если мы возьмем фунт зернистого пороху, вспыхивающего при зажигании мгновенно, спрессуем его под большим давлением в форму цилиндра, то увидим, что горение не сразу охватить цилиндр, а будет распространяться довольно медленно от одного конца к другому и с определенной скоростью. Скорость распространения горения в прессованном порохе определена из многочисленных опытов и составляет 4 линии в секунду.
„На этом свойстве прессованного пороха основано устройство боевых ракет. Сущность этого устройства состоит в следующем. В жестяной цилиндр, закрытый с одного основания и открытый с другого, вставляется плотно цилиндр из прессованного пороха, имеющий по оси пустоту в вице сквозного канала; горение прессованного пороха начинается с поверхности этого канала и распространяется в течение определенного промежутка времени к наружной поверхности прессованного пороха; образующиеся при горении пороха газы производят давление во все стороны, но боковые давления газов взаимно уравновешиваются, давление же на дно жестяной оболочки пороха, не уравновешенное противоположным давлением (так как в эту сторону газы имеют свободный выход), толкает ракету вперед по тому направлению, на котором она была установлена в станке до зажигания. Траектория полета ракеты составляет параболу, подобно траектории ядер, выпущенных из орудий.
„Представим себе теперь, что мы имеем из листового железа цилиндр известных размеров, закрытый герметически со всех сторон и только в нижнем дне своем заключающий отверстие известной величины. Расположим по оси этого цилиндра кусок прессованного пороха цилиндрической же формы и зажжем его с одного из оснований; при горении образуются газы, которые будут давить на всю внутреннюю поверхность металлического цилиндра, но давление на боковую поверхность цилиндра будет взаимно уравновешиваться, и только давление газов на закрытое дно цилиндра не будет уравновешено противоположным давлением, так как с противоположной стороны газы имеют свободный выход через отверстие в дне. Если цилиндр поставлен закрытым дном кверху, то, при известном давлении газов, величина которого зависит с одной стороны от внутренней емкости цилиндра, а с другой — от толщины куска прессованного пороха, цилиндр должен подняться вверх".
Затем следуют некоторые технические детали проекта. К своему проекту Кибальчич приложил чертеж прибора, который мы здесь воспроизводим (см. рис.). Действие его объясняется в записке так:
„В цилиндре А, имеющем в нижнем дне отверстие С, устанавливается по оси, ближе к верхнему дну, пороховая свечка Д" (так я буду называть цилиндрики из прессованного пороха). Цилиндр А посредством стоек NN прикреплен к средней части платформы Р, на которой стоит воздухоплаватель... Представим теперь, что свечка К зажжена. Через очень короткий промежуток времени цилиндр А наполняется горячими газами, часть которых давит на верхнее дно цилиндра, и если это давление превосходит вес цилиндра, платформы и воздухоплавателя, то прибор должен подняться вверх".

Проект реактивного летательного прибора Н. И. Кибальчича (с собственноручного наброска).
К главе IХ
8. «Ракета» Циолковского
В наши дни идея реактивного аппарата для межпланетных полетов далека еще не только от практического осуществления, но даже и от теоретического воплощения в форме технического проекта. Пройдут, вероятно, сотни лет — писал К. Э. Циолковский в 1911 г., — прежде чем высказанные мною взгляды найдут применение и люди воспользуются ими, чтобы расселиться не только по лицу Земли, но и во всей Вселенной"[37]. Однако, чтобы дать наглядный пример одной из возможных форм осуществления основного принципа, привожу набросанный, по моей просьбе, К. Э. Циолковским схематический чертеж изобретенного им снаряда и краткое, составленное им, пояснение:
„Снаряд имеет снаружи вид бескрылой птицы, легко рассекающей воздух. Большая часть внутренности занята двумя веществами в жидком состоянии; водородом и кислородом. Они разделены перегородкой и соединяются между собой только мало-по-малу. Остальная часть камеры, меньшей вместимости, назначена для помещения наблюдателя и разного рода аппаратов, необходимых для сохранения его жизни, для научных наблюдений и для управления Ракетой. Водород и кислород, смешиваясь в узкой части постепенно расширяющейся трубы (в роде духового музыкального инструмента), соединяются химически и образуют водяной пар при страшно высокой температуре. Он имеет огромную упругость и вырывается из широкого отверстия трубы с ужасающею скоростью по направлению трубы или продольной оси камеры. Направление давления пара и направление полета снаряда прямо противоположны".
Пополним это описание некоторыми подробностями, заимствованными из научной повести К. Э. Циолковского ,,Вне Земли" (Калуга, 1920):
„Камеры взрывания и трубы, составляющие их продолжение, были сооружены из весьма тугоплавких и прочных веществ, вроде вольфрама[38]"; также и инжекторы [для накачивания элементов взрыва]. Весь взрывной механизм окружался камерой с испаряющейся жидкостью, температура которой была поэтому достаточно низкой. Эта жидкость была одним из элементов взрывания. Другая жидкость помещалась в других изолированных отделениях.
„Наружная оболочка Ракеты состояла из трех слоев. Внутренний слой — прочный металлический с окнами из кварца, прикрытыми еще слоем обыкновенного стекла, и с дверями, герметически закрывающимися. Второй — тугоплавкий, но почти не проводящий тепла. Третий, наружный, представлял очень тугоплавкую, но довольно тонкую металлическую оболочку. Во время стремительного движения Ракеты в атмосфере наружная оболочка накалялась добела, но теплота эта излучалась в пространство, не проникая сильно через другие оболочки внутрь. Этому еще мешал холодный газ, непрерывно циркулирующий между двумя крайними оболочками, пронизая рыхлую, мало теплопроводную, среднюю прокладку.

Схематический набросок проекта межпланетного дирижабля Циолковского (в разрезе).
Труба А и камера из прочного тугоплавкого металла покрыты внутри еще более тугоплавким материалом, — напр., вольфрамом. С и D — насосы, накачивающие жидкий кислород и водород в камеру взрывания В. „Ракета" еще имеет вторую наружную тугоплавковую оболочку. Между обоими оболочками, есть промежуток FFF, в который устремляется испаряющийся жидкий кислород в виде очень холодного газа; он препятствует чрезмерному нагреванию обоих оболочек от трения при быстром движении „Ракеты" в атмосфере. Жидкий кислород и такой же водород разделены друг от друга непроницаемой оболочкой (не изображенной на чертеже). I — труба, отводящая испаренный холодный кислород в промежуток между двумя оболочками; он вытекает наружу через отверстие КК. У отверстия трубы А имеется (не изображенный на чертеже) руль из двух взаимно перпендикулярных плоскостей для управления „Ракетой"; вырывающиеся разреженные и охлажденные газы, благодаря этим рулям, изменяют направление своего движения и таким образом поворачивают „Ракету".
„Сила взрывания могла регулироваться с помощью инжекторов, а также прекращаться и возобновляться. Этим и другими способами можно изменять направление оси снаряда и направление взрывания.
„Температура внутри Ракеты регулировалась, по желанию с помощью кранов, пропускающих холодный газ через среднюю оболочку. Из особых резервуаров выделялся газ, необходимый для дыхания. Другие снаряды были назначены для поглощения продуктов выделения кожи и легких человека. Были камеры с запасами для пищи и воды. Были особые скафандры, которые надевались при выходе в пустое пространство и вхождении в чуждую атмосферу другой планеты. Были камеры с жидкостями для погружения в них путешествующих во время усиленной относительной тяжести; погруженные в них люди дышали через трубку, выходящую в воздушную атмосферу Ракеты. Жидкость уничтожала их вес, как бы он ни был велик в краткое время взрывания. Люди совершенно свободно шевелили всеми своими членами, даже не чувствовали их веса, как он чувствуется на Земле: они были подобны купающемуся, — или же прованскому маслу в вине при опыте Плато...
„Объем Ракеты составлял около 800 куб. метров. Менее третьей доли этого объема (240 к. м.) было занято двумя постепенно взрывающимися жидкостями. Этой массы было довольно, чтобы 50 раз придать Ракете скорость, достаточную для удаления снаряда навеки от солнечной системы и вновь 50 раз потерять ее. Такова была сила взрывания этих материалов. Вес оболочки или самого корпуса Ракеты со всеми принадлежностями был равен 40 тоннам; запасы, инструменты, оранжереи составляли 30 тонн. Люди и остальное — менее 10 тонн. Следовательно, вес Ракеты со всем содержимым был в три раза меньше веса взрывчатого материала. Объем для помещения людей, т. е. заполненного разреженным кислородом пространства, составлял около 400 куб. метров. Предполагалось отправить в путь 20 человек. На каждого доставалось помещение в 20 куб. метров, или около двух куб. сажен..."
Так рисуется в мечтах изобретателя этот межпланетный дирижабль будущего. Желающих познакомиться с работами и идеями К. Э. Циолковского[39] подробнее отсылаем к его печатным трудам:
1. „Исследование мировых пространств реактивными приборами" — напечатано в кратком виде в „Научном Обозрении", (1903, май) и более пространно в „Вестнике Воздухоплавания" (1911 г. №№ 19 — 22 и 1912 г., №Ns 2 — 9).
2. Дополнение к этой работе, напечатанное под тем же заглавием отдельной брошюрой (Калуга, 1914).
3. „Вне Земли" — научная повесть, описывающая воображаемое межпланетное путешествие с помощью реактивного прибора. Печаталась в сокращенном виде в журнале „Природа и Люди" в 1918 г. (не была закончена) и выпущена в полном виде отдельной книгой в 1920 г. в Калуге местным Обществом Изучения Природы.
К главе IX
9. Проект Графиньи
Укажем, ради полноты, на еще один проект межпланетных путешествий, предложенный в 1915 г. известным французским писателем по вопросам воздухоплавания Анри Графиньи (а еще ранее указанный французами Мас и Друэ). По существу он представляет вариант идеи реактивного снаряда, только получающего свою начальную скорость иным путем.
„Представьте себе колесо огромного диаметра, несущее на окружности снаряд, который должен быть отброшен вдаль. Если при достаточной скорости вращения внезапно освободить снаряд, — он полетит по касательной с той же скоростью, с какой двигалась соответствующая точка колеса. Устройство может быть еще упрощено: машина может состоять из двух параллельных брусьев, закрепленных посредине на оси. Противоположные концы брусьев могут быть снабжены с одной стороны, метательным снарядом, с другой — противовесом. При длине брусьев в 100 метров каждый оборот даст путь в 314 метров; значит, если довести скорость вращения до 44 оборотов в секунду, то крайние точки будут двигаться с секундного скоростью около 14 километров.
„Если пожелаем развить эту скорость в течение нескольких минут, понадобится двигатель, мощностью в миллион лошадинных сил. Это, очевидно, неприемлемо. Оставаясь в пределах существующих технических возможностей, придется действовать медленнее и положить, примерно, семь часов, чтобы добиться 44 оборотов в секунду; тогда достаточен будет двигатель в 12000 лошадиных сил.
„Такая метательная машина должна быть расположена где-нибудь над расщелиной, — напр., между скалами в горах. Она будет приводиться в движение от паровой турбины; а в нужный момент особое электрическое приспособление освободит закрепленный на колесе снаряд, который и полетит вертикально, к зениту...
„Корабль вселенной должен быть снабжен внутренним двигателем, позволяющим увеличить его собственную скорость и управлять его движениями; двигатель не должен быть вовсе особенно сильным, — аппарат, изолированный в пространстве, перемещается с большою легкостью. Мы разумеем двигатель с отдачей", основанный на принципе ракеты; он выбрасывает в пространство массу газа, истечение которого заставит аппарат отклониться.
„Первым следствием работы подобного двигателя является сообщение кораблю постоянно увеличивающейся скорости; это значительно уменьшает длительность межпланетных путешествий. Вторым следствием является замена исчезнувшей силы тяжести ускорением. Мы знаем из опыта, что у человека, поднимаемого кверху с возрастающею скоростью, получается ощущение усиленной тяжести; тот же результат получается и для пассажиров небесного снаряда — они избавятся, благодаря ему, от неприятного ощущения, словно они реют без всякого веса...
„Вес аппарата такого типа достигнет 75 пудов; внутреннее оборудование может быть исчислено в 40 пудов — так что полный вес снаряда — 115 пудов. Прибавляя этот вес к весу провизии на два месяца и трех пассажиров, получим общий вес около 240 пудов.
„Осуществление всего этого не превосходит того, что может быть достигнуто человеческой техникой. Что такое, в самом деле, наш двойной 100-метровый стержень, приводимый в действие двигателем в 12000 лошадиных сил, по сравнению с башней Эйфеля (300 метров) или паровыми двигателями „Лузитании"?
„Можно было бы начать с более скромных опытов. Громадную начальную скорость может дать колесо, даже в 10 раз меньшее, нежели вышеописанное. Можно придать ему скорость в 400 оборотов в секунду помощью турбины типа Лаваля. В шесть часов скорость может быть доведена до 6 километров въ секунду. Такой снаряд может быть отброшен на многие тысячи километров над земной поверхностью — для заатмосферных исследований огромного научного интереса (помощью самозаписывающих аппаратов): ведь мы не знаем даже, что совершается на высоте 60 километров над нашими головами".
К главе X
10. Невесомость падающих тел
Положение, что свободно падающее (или брошенное) тело ничего не весит, представляется многим настолько необычным и неожиданным, что его готовы принять за физический софизм (вывод правдоподобный, но ложный). Уместно будет поэтому указать на несколько опытов, могущих подтвердить правильность этого утверждения.
Целый ряд опытов подобного рода был впервые выполнен около 1892—1893 гг. московским физиком проф. Н. А. Любимовым. Из этих остроумных опытов, — странным образом преданных забвению[40] — укажем следующие:
1. Маятник с твердым стержнем, привешенный к вертикальной доске, отводится в сторону и удерживается в этом положении штифтом. Когда доске с этим маятником дают свободно падать, вынув штифт, удерживавший маятник, то он остается в отклоненном положении, не обнаруживая стремления раскачиваться[41].
2. К такой же доске прикрепляют стеклянную трубку, в наклонном положении: вверху трубки кладут на ее скошенный край тяжелый шарик, удерживаемый штифтом. В момент падения доски штифт удаляют, — но шарик остается вверху трубки, не скатываясь внутрь ее.
3. На той же доске укрепляют магнит, а под ним на полочку кладут железную полоску (якорь) в таком расстоянии, чтобы магнит не мог ее поднять. Во время падения доски с магнитом и якорем последний притягивается магнитом (так как невесомый якорь уже не надавливает на пружину).
4. „Закон Архимеда утрачивает свое значение при падении системы. Представим себе, что в сосуд с водою погружена пробка (см. рис.). Пружина удерживает ее в воде вопреки давлению жидкости снизу вверх, повинуясь которому пробка всплыла бы наверх. Во время падения сосуда с пробкою этого давления снизу вверх нет [так как давление жидкости обусловлено в данном случае ее весомостью], и пробка опускается вниз". (Н. А. Любимов. „К физике системы, имеющей переменное движение").

Один из опытов проф. Н. А. Любимова: отмена закона Архимеда в падающей системе.
„Явления того же порядка — пишет Н. А. Любимов в сейчас упомянутой брошюре — могут быть наблюдаемы, в известной степени, не только при свободном падении системы, но и в системе, катящейся вниз по наклонной плоскости или качающейся. Опыты с катящейся по наклонной плоскости или качающейся системой могут быть произведены тем с большим удобством, что наблюдатель сам может поместиться в скатывающейся или качающейся системе (катиться с горы, качаться на качелях) и следить за явлением. Нет особого затруднения устроить и свободно падающую систему с помещенным в ней наблюдателем, озаботившись, чтобы падающая система, — напр., корзина на перекинутой через блок веревке — достигала земли без толчка, с утраченною уже скоростью"[42].
Вопрос этот — несмотря на элементарность — почти не затрагивается ни в большинстве учебников, ни в общедоступных книгах по физике. Укажем поэтому несколько сочинений, в которых он рассматривается с той или иной стороны (начинаем с более популярных):
В. Л. Розенберг. Первые уроки физики. 1914.
Я. И. Перельман. Занимательная физика. 1922.
К. Э. Циолковский. Грезы о земле и небе. 1895.
Н. А. Любимов. К физике системы, имеющей переменное движение. 1893.
Герман Ган. Физические опыты. Русск. перевод в изд. «Физика Любителя». 1911. Ч. I. § 48. Сила тяжести.
А. Поспелов. Об относительной потере веса тел в падающей системе. 1913.
Его же. Мир переменной весомости тел. 1913.
К главе X
11. Жизнь при отсутствии тяжести.
По поводу настоящей книжки в печати и в письмах к автору высказывалось опасение, что последствия для живого организма от помещения его в среду без тяжести должны быть роковыми. Опасения эти, однако, ни на чем, в сущности, не основаны. Если обстоятельно и систематически рассмотреть, какие именно функции нашего организма могли бы серьезно расстроиться вследствие утраты веса, то окажется, что таких функций нет. „Во время падения или простого прыжка на нашей планете, пока мы еще не коснулись ногами ее почвы, мы также находимся, по отношению к нашему телу, одежде и предметам, при нас находящимся, в среде, свободной от тяжести, но явление это продолжается много-много полсекунды; в течение этого промежутка времени части нашего тела не давят друг на друга, пальто не отягчает плеч, часы не оттягивают кармана. При купании на земле вес нашего тела также почти парализуется противоположным действием воды. Такое отсутствие веса может уже продолжаться неопределенно долгое время. Отсюда видно, что едва ли нужны какие-либо особые опыты для доказательства безвредности среды, лишенной тяжести.
„Если бы даже оказалось, что люди не могут жить без тяжести, то ее легко было бы создать искусственно в среде, где ее нет. Для этого надо только Ракете сообщить вращательное движение; тогда, вследствие центробежной силы, образуется кажущаяся тяжесть желаемой величины, в зависимости от размеров ракеты и скорости ее вращения. Эта тяжесть тем удобна, что может быть произвольно мала или велика, всегда может быть уничтожена и опять возобновлена; но она, как и естественное тяготение, требует усиленной крепости вращающейся Ракеты и других предметов, так как стремится их разрушить (К. Циолковский, „Исследование мировых пространств"[43]).
Отметим еще неправильность соображения (высказанного некоторыми критиками), будто невесомый воздух внутри межпланетного дирижабля не должен оказывать никакого давления. Если бы это было верно, то, конечно, целый ряд явлений внутри небесного корабля происходил бы не так, как описано в главе X. Но в действительности давление воздуха при данных условиях нисколько не связано с его весомостью. Весомость, конечно, была причиною того, что воздух близ земной поверхности сжат и давит во все стороны. Но этот сжатый воздух должен полностью сохранить свое давление и в том случае, если, в закрытом помещении, он становится невесомым. Ведь сжатая пружина не утрачивает своей упругости в среде без тяжести. Карманные часы не изменят своего хода от перенесения с Земли на Луну или на самый маленький астероид. Сжатый газ — та же пружина, и не должен утрачивать своей упругости при ослаблении тяжести или полной потере веса (если, конечно, газ заключен в герметически замкнутом пространстве). Поэтому барометр-анероид показал бы в летящем небесном дирижабле то же самое давление, какое он показывал там до отлета. Барометр же ртутный не пригоден в таких условиях потому, что он измеряет давление воздуха весом ртутного столба, который в среде без тяжести равен нулю.
К главе X
12. Межпланетная сигнализация.
В связи с вопросом о возможности межпланетных сообщений интересно коснуться и другой, естественно связанной с ним темы — межпланетных сношений помощью оптических или иных сигналов. Мы ограничимся здесь беглой справкой.
Впервые в серьезной форме вопрос этот был поставлен в первой половине XIX века знаменитым германским математиком Гауссом. Немецкий астроном Груитуйзен, горячий сторонник обитаемости Луны разумными существами, излагает проект Гаусса так:
„Вот основная идея Гаусса; нужно показать жителям Луны то геометрическое построение, с помощью которого обыкновенно доказывается Пифагорова теорема. Средство — культура земной поверхности где-нибудь на громадной равнине. Чтобы изобразить геометрические фигуры, нужно пользоваться контрастом между темными полосами лесов и золотисто-желтыми площадями хлебных полей. Это удобнее сделать в стране, где жители только временно пользуются обрабатываемой землей и, следовательно, легко подчиняются указаниям. Таким образом, выполнение данной мысли не потребовало бы чрезмерных затрат. Гаусс говорил об этом с глубокой серьезностью. Он придумал еще один способ завязать сношения с обитателями Луны. Способ состоит в применении гелиотропа, — прибора, изобретенного Гауссом и могущего служить не только для измерения углов с весьма длинными сторонами, но и для подачи сигналов. По мысли Гаусса, нет даже необходимости составлять из зеркал громадную отражающую поверхность: достаточно известного числа хорошо обученных людей с самыми обыкновенными зеркалами. Следует выбрать время, когда обитатели Луны наверное смотрят на Землю, — например, когда наша планета покрывает Венеру. Зеркала отбрасывают свет по направлению к Луне. Чтобы жители Луны узнали о нашем существовании, нужно прерывать этот свет через равные промежутки времени; так можно сообщить им числа, которые имеют большое значение в математике. Конечно, чтобы эти знаки привлекли внимание, нужно выбрать, подходящий день, когда яркость света, отраженного гелиотропом, будет особенно велика. Гаусс предпочитал математические знаки, потому что у нас и у обитателей далеких миров могуг оказаться общими только основные математические понятия и воззрения".
Попыток осуществить этот проект не делалось.
В 1890-м году много и оживленно обсуждался вопрос о сношении, помощью оптических сигналов, с предполагаемыми обитателями Марса. При таком настроении умов некоторые замеченные на нем явления были приняты за световые сигналы. ,,Как раз в то время, когда пылкие умы старались измыслить средства, чтобы установить сношения между планетами, некоторые наблюдатели, вооруженные весьма сильными телескопами, заметили своеобразные светлые выступы на границе освещенной и ночной половин Марса. Выступы эти держались слишком долго, чтобы их можно было принять за цепь облаков; казалось, обширные области планеты начинали светиться, едва над ними опускалась ночь... Для многих не оставалось сомнения, что здесь мы усматриваем огненные знаки с этого далекого мира. К сожалению, это не подтвердилось: Кемпбелл вполне понятным образом объяснил появление этих светлых выступов, как обширные горные области [залитые светом]... В 1892 г. и 1894 г. светлые места наблюдались опять. Они появлялись всегда в определенных местах, именно лишь в тех желтых областях, которые астрономы считают материками. Кемпбелл дает следующее объяснение этому явлению: „Марс находился от нас на расстоянии 63 миллионов километров. Мы могли брать увеличения в 350 — 520, и планета приближается к нам на расстояние в 180.000 км. и 120.000 км. Расстояние Луны от нас вдвое и втрое больше. Однако, мы можем просто глазом видеть на границе дневной и ночной половин светлые выступы, образуемые горными цепями и большими кратерами" (В. Мейер, „Мироздание"). — Сходные наблюдения и толки повторились и в декабре 1900 г., когда американский астроном Дуглас заметил на Марсе яркое пятно, державшееся в течение часа. Изобретение беспроводного телеграфа направило мысль о межпланетных сношениях на новый путь. Особенно много говорилось об этом в конце 1900 гсда, когда знаменитый американский электротехник Тесла сообщил, что ему удалось заметить загадочные электрические сигналы при производстве опытов на большой высоте. „Тесла наблюдал — читаем мы в английском научном журнале 1901 г. — на специальном приборе повторные электрические колебания, причина которых заставляла его теряться в догадках. Он пришел к мысли, что они обязаны своим происхождением токам, идущим от планет, и теперь он полагает, что было бы вполне возможно посредством усовершенствованного аппарата сноситься с их обитателями. Далее, со слов Тесла, сообщалось, что он приступает к постройке аппарата, "который даст возможность послать на Марс количество энергии, достаточное для воздействия на электрические приемники, в роде телеграфов и телефонов „Я не сомневаюсь — писал Тесла, — что помощью надлежащим образом построенного аппарата возможно переслать энергию на другие планеты, например, на Марс и Венеру, даже при наибольшем их удалении от Земли. Мой метод даст практическое разрешение вопроса передачи и получения сообщений с планет". Однако, эти предположения ни к чему не привели, и вызванная заявлением Тесла горячая полемика в печати вскоре прекратилась[44].
Оживление интереса к этой проблеме наступило вновь лишь в самое последнее время. В 1920 и 1922 г. неоднократно отмечались случаи приема радиостанциями таких сигналов, для которых, по некоторым соображениям, затруднительно допустить земное происхождение; это обстоятельство — в связи с тем, что сигналы наблюдались как раз в эпохи наибольшей близости Марса к Земле — побудило искать станцию отправления загадочных сигналов именно на этой планете.
Интересно поэтому рассмотреть, какие физические и технические трудности стоят на пути к осуществлению радиосвязи с планетами на практике.
Прежде всего надо указать, что хотя на земной поверхности для современного радиотелеграфа более не существует уже непреодолимых расстояний, — но передаваться вверх электрические волны могут беспрепятственно всего лишь сотни на две верст. Дело в том, что на высоте 50 — 200 верст простирается слой разреженной атмосферы, отличающийся от нижележащих своею значительною электропроводностью. Такой слой непрозрачен для электрических волн: он частью отражает падающие на него электрические лучи назад, частью поглощает их, не выпуская наружу. Этот экран, охватывающий непроницаемой оболочкой весь земной шар, прозрачен до некоторой степени лишь для тех электрических лучей, которые направлены к точке зенита, — но энергия ослабленных волн, проникающих через зенитное окошечко, чересчур ничтожна, чтобы заставить работать аппараты отдаленных станций. Допустим, — ради внесения определенности в задачу — что чувствительность марсовых приемников одного порядка с чувствительностью самых совершенных земных аппаратов; тогда, для успешной передачи сигнала на Марс потребовалась бы, согласно вычислениям специалистов, радиотелеграфная станция не менее чем в 15.000.000 лошадиных сил! Грандиозность такого результата выступит яснее, если напомнить, что величайшая современная радиостанция (в Сан-Франциско) обладает мощностью всего в 10.000 лош. сил, и что совокупная мощность всех механических двигателей русской промышленности довоенного времени не превосходила 5 миллионов лош. сил. Межпланетная радиостанция поглощала бы угля втрое больше, чем все фабрики и заводы России вместе, работая в довоенном масштабе! Если бы вся энергия Ниагарского водопада полностью была употреблена на вращение якоря динамо-машины, то и тогда мы не получили бы мощности, достаточной для передачи радио-сигнала на Марс. Такие же затруднения вероятно, возникли бы и для обитателей Марса, если бы они пожелали установить радиосвязь с нами (их электрические волны, уже проникшие через непроницаемый слой атмосферы Марса, должны были бы отразиться от непроницаемой для электрических лучей наружной оболочки нашей атмосферы). При таких условиях питать надежды на близкую осуществимость радиотелеграфной связи с планетами, конечно, не приходится.
